微分

1 连续性

众所周知微分的几何意义是斜率，然而斜率最初的定义只涉及直线，指的是$y=kx+b$中的$k$，而对任意曲线$y=f(x)$而言，若想谈其斜率，就必须先做出其切线，换句话说，$y=f(x)$其在$x_0$点的导数，是$f(x)$在$x_0$点的切线的斜率。

从几何的视角去看，$y=f(x)$在$x_0$点的切线首先要过$x_0$点，然后要求在足够小的区间内，和$f(x)$方向一致，从而才能说二者切在了一起。而所谓方向一致，直观的说法就是，在这个足够小的区间内，二者几乎重合。就像此前画的$\sin x$和$x$在$x=0$附近的那张图一样。

这意味着，并非所有的函数都在任意点处存在切线。最直观的例子就是随机函数，对于$y=r(x)$来说，任何一点都随机地对应$(0,1)$区间中的某个点，由于这种对应足够稠密，任何位置都没有切线。

比如下面这个随机函数

x = seq(0,0.1,0.01)
y = runif(11,0,1)
plot(x,y)
lines(x,y)

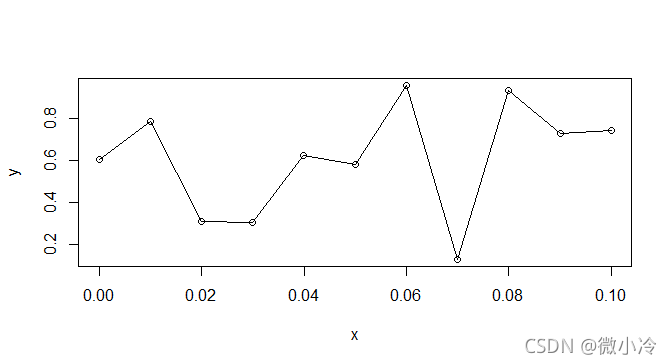
尽管看上去任意一点都可画出一条不与相邻点相交的直线，但问题在于，我们所绘制的这个图只是对随机函数的一个抽样，在其任意相邻的两个点的中间，都有无穷多个$(0,1)$区间内的点，所以无论在$x_0$处绘制一条怎样的曲线，对于任意小的$\epsilon$，我们都能找到一点$(x,f(x))$，满足$|x-x_0|<\epsilon$的同时，$(x_0,f(x_0))$到$(x,f(x))$没有任何重合的意图。

这个案例启发我们必须对函数进行一次划分，把随机函数这种过于混乱的东西从我们的研究对象中剔除，从而我们需要引入连续的概念。

对于$r(x)\in (0,1)$的随机函数来说，对任意一点$x_0$，我们创建一个任意小的区间$[x_0-\epsilon ,x_0+\epsilon ]$，这个区间的值域恒为$(0,1)$，如果我们画出$(0,0.01)$区间内的1000个点，那么大致是这样的

x = seq(0,0.01,0.00001)
y = runif(1001,0,1)
plot(x,y)

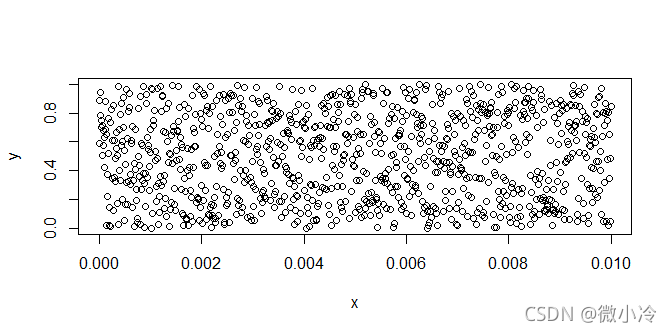
无论我们把区间缩小到什么程度，这种乱糟糟的仿佛要铺满整个坐标图的点的样式并不会发生变化。

但直线$y=x$却非如此，对任意一点$x_0$，我们创建一个任意小的区间$[x_0-\epsilon ,x_0+\epsilon ]$，这个区间的值域为$(x_0-\epsilon ,x_0+\epsilon )$，随着$\epsilon$的不断缩小，这个区间也不断地趋近于0。

由此，我们可以定义连续函数：即随着定义域的区间长度趋近于0，则值域的区间长度也趋近于0的函数。

区间长度趋近于0就意味着区间内的元素个数越来越少，甚至到了常数个，乃至剩下最后一个。也就是说，随着$x\to x_0$，必有$f(x)\to f(x_0)$。这就是最常见的连续性的定义

$$\underset{x\to x_0}{\lim }f(x)=f(\underset{x\to x_0}{\lim }x)=f(x_0)$$

需要注意的是，上式中，$f({\lim }_{x\to x_0}x)=f(x_0)$之所以成立，乃因$f(x)=x$是不证自明的连续函数。

把一个连续函数变成不连续的函数十分简单，只要把其中任意一个点扣掉就可以了，例如函数$y=f(x)$显然是连续的，但下面这个函数就显然不连续。

$$f(x)=\{\begin{array}{rl}x,& x\ne 0\\ 1,& x=0\end{array}$$

或者把一个连续的函数撕成两半，比如下面这个

$$f(x)=\{\begin{array}{rlr}& x,& x>0\\ & x+1,& x\le 0\end{array}$$

而这个函数在$x=0$的时候又有了一个奇怪的性质，即

$$\begin{array}{r}\underset{x\to x_{+}}{\lim }f(x)=0\ne f(0)\\ \underset{x\to x_{-}}{\lim }f(x)=1=f(0)\end{array}$$

也就是说，$f(x)$从左边趋近于0的时候，f(x)在0处是连续的，而在右侧趋近于0的时候，却并不连续。此即左连续和右连续的概念。

2 求导

回到切线的问题，如果曲线$y=f(x)$在$x_0$点并不连续，那么这点显然没有唯一的一条切线。

有的时候，尽管满足了连续性的要求，也不一定存在切线，比如

$$y=|x|$$

x = seq(-10,10)
y = abs(x)
plot(x,y,type='l')

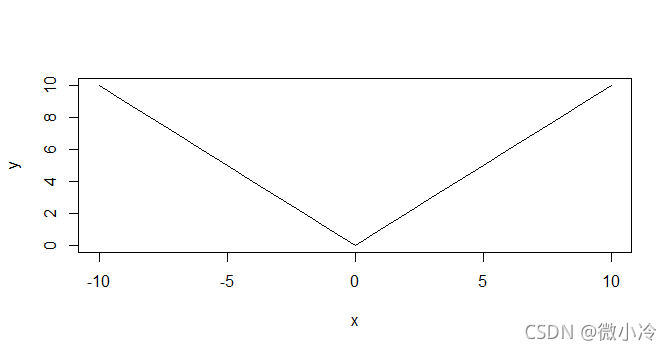
在$x=0$的位置，我们找到的切线要么和左边重合，要么和右边重合，也就是说这个函数在$x=0$处存在两条切线。

同时也就意味着这一点有两个斜率，两个导数。所以，如果把导数定义为某种映射，则一个点不可能映射为两个导数，所以宁愿让这点的导数不存在。

这种为了保证映射成立而舍弃某个值的做法并不罕见，早在中学时代，$\sqrt{N}$就是个典型的例子，在定义偶数次根的时候，我们把负值舍弃了。但这里做得更绝，左右两端的值都被舍弃了，从而被判定不可导。

在对求导有了直观的几何印象之后，我们再来用分析的语言表述何谓“在足够小的区间内几乎重合”。

对于曲线$y=f(x)$，在$x=x_0$处的切线为$y=kx+b$，则满足

$$\underset{\epsilon \to 0}{\lim }f(x_0+\epsilon )-[k(x_0+\epsilon )+b]=0$$

由于二者在$x_0$点重合，即$f(x_0)=k{x}_0+b$这个式子可以写为

$$\underset{\epsilon \to 0}{\lim }f(x_0+\epsilon )=\underset{\epsilon \to 0}{\lim }[k{x}_0+b+k\epsilon ]=\underset{\epsilon \to 0}{\lim }[f(x_0)+k\epsilon ]$$

整理可得

$$k=\underset{\epsilon \to 0}{\lim }\frac{f(x_0+\epsilon )-f(x_0)}{\epsilon }$$

$k$就是导数。写成我们熟悉的形式就是

$$f^{\prime }(x_0)=\underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$$

若将$\text{d}x$定义为$x$的微小变化量，$\text{d}y$定义为$y$的微小变化量，则导数可以写成微分的形式

$$f^{\prime }(x_0)=\frac{\text{d}y}{\text{d}y}{|}_{x=x_0}$$