1. 二叉树的前序遍历 (中，后序类似)

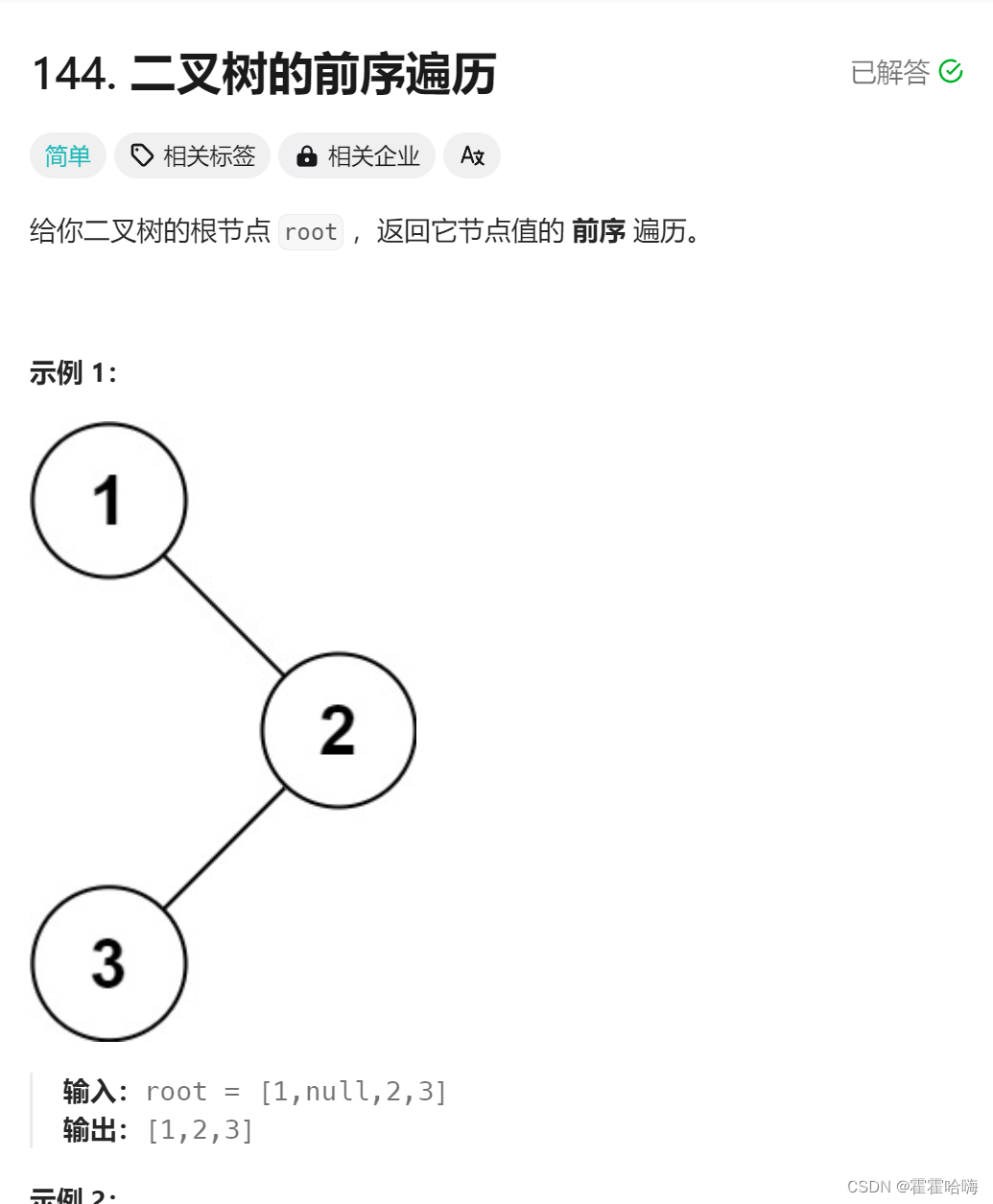
这道题的意思是对二叉树进行前序遍历，把每个结点的值都存入一个数组中，并且返回这个数组。

思路：
这题与我们平时写的二叉树前序遍历不同。需要我们自己开辟空间，但又由于二叉树结点个数未知，所以在开辟空间之前要先计算结点个数，根据结点个数开辟空间。最后再利用分治递归进行前序遍历。

代码实现如下：

注意：
(1) 结点个数的计算，数组空间的开辟；
(2) 递归时一般用子函数 _prevOrder 递归，而不是 preorderTraversal 原函数，不然会重复的开辟空间；

(3) 局部变量 i 一定要传地址，因为每一层递归函数都有一个 i ，下一层放的 i 是 i++之后的 i ，由于形参是实参的一份临时拷贝，若不传地址，就不会影响上一层函数中的 i ，就是加的不是同一个 i ；

(4) 输出型参数 returnSize ，目的是获取a数组有多大。

//前序遍历
void _prevOrder(struct TreeNode* root, int* a, int* pi)
{
    if (root == NULL)
        return;

    a[*pi] = root->val;
    (*pi)++;

    _prevOrder(root->left, a, pi);
    _prevOrder(root->right, a, pi);
}

//由于不知道数组开多大的空间，所以要提前计算树的结点个数
int TreeSize(struct TreeNode* root)
{
    return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

int* preorderTraversal(struct TreeNode* root, int* returnSize) {
    int size = TreeSize(root);

    //开辟数组空间
    int* a = (int*)malloc(sizeof(int) * size);

    int i = 0;
    _prevOrder(root, a, &i);

    *returnSize = size;

    return a;
}

2. 二叉树的最大深度

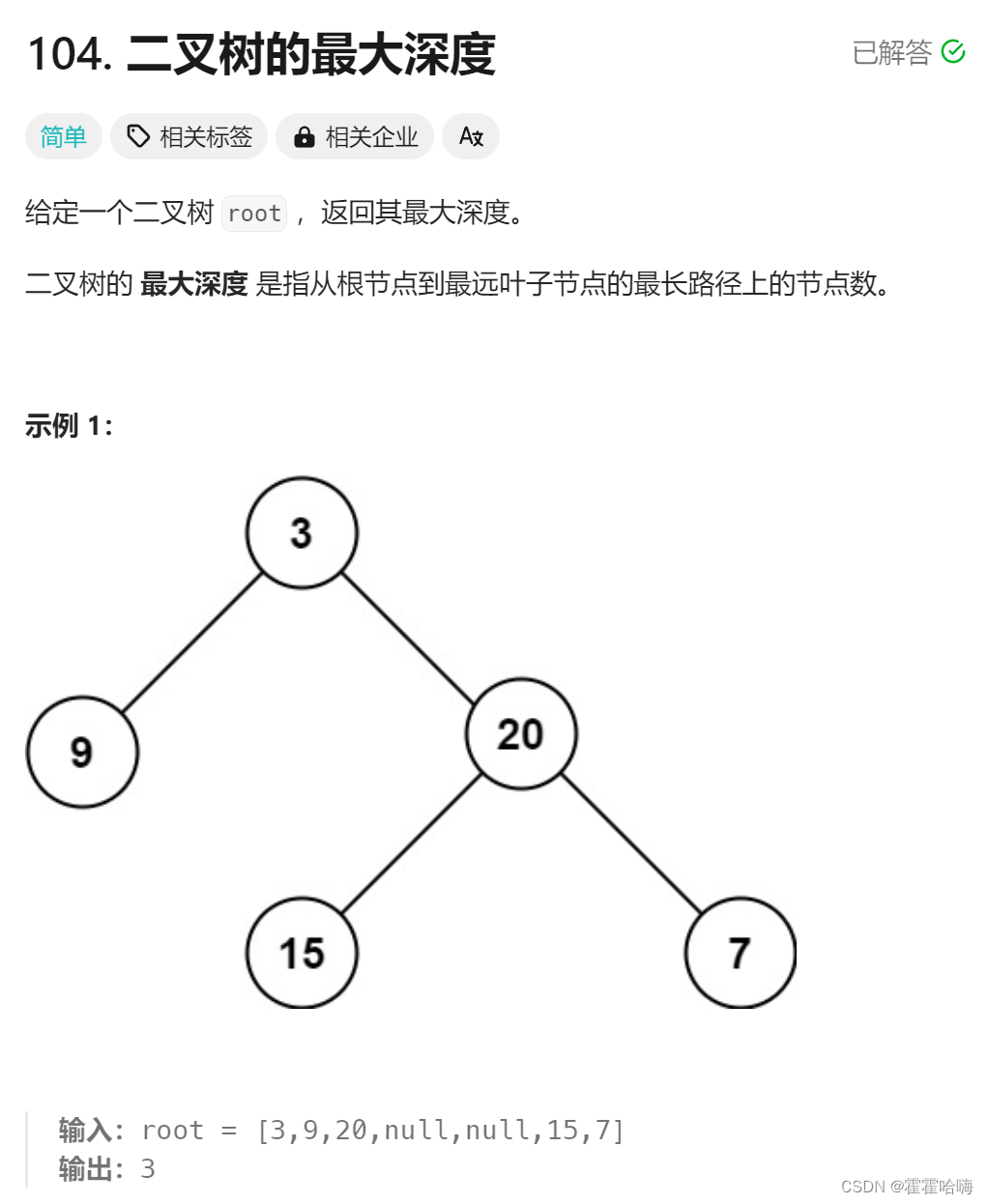
思路：
利用分治递归思想。若根节点为空，则深度为0；若非空，则先求左右子树的深度，我的深度 = 左右子树深度大的 + 1。

代码实现如下：

注意：
要先用两个变量记录计算好的左右子树的深度！不然运行时会超出时间限制。

int maxDepth(struct TreeNode* root) {
    if (root == NULL)
    {
        return 0;
    }

    int leftDepth = maxDepth(root->left);
    int rightDepth = maxDepth(root->right);

    return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}

3. 平衡二叉树

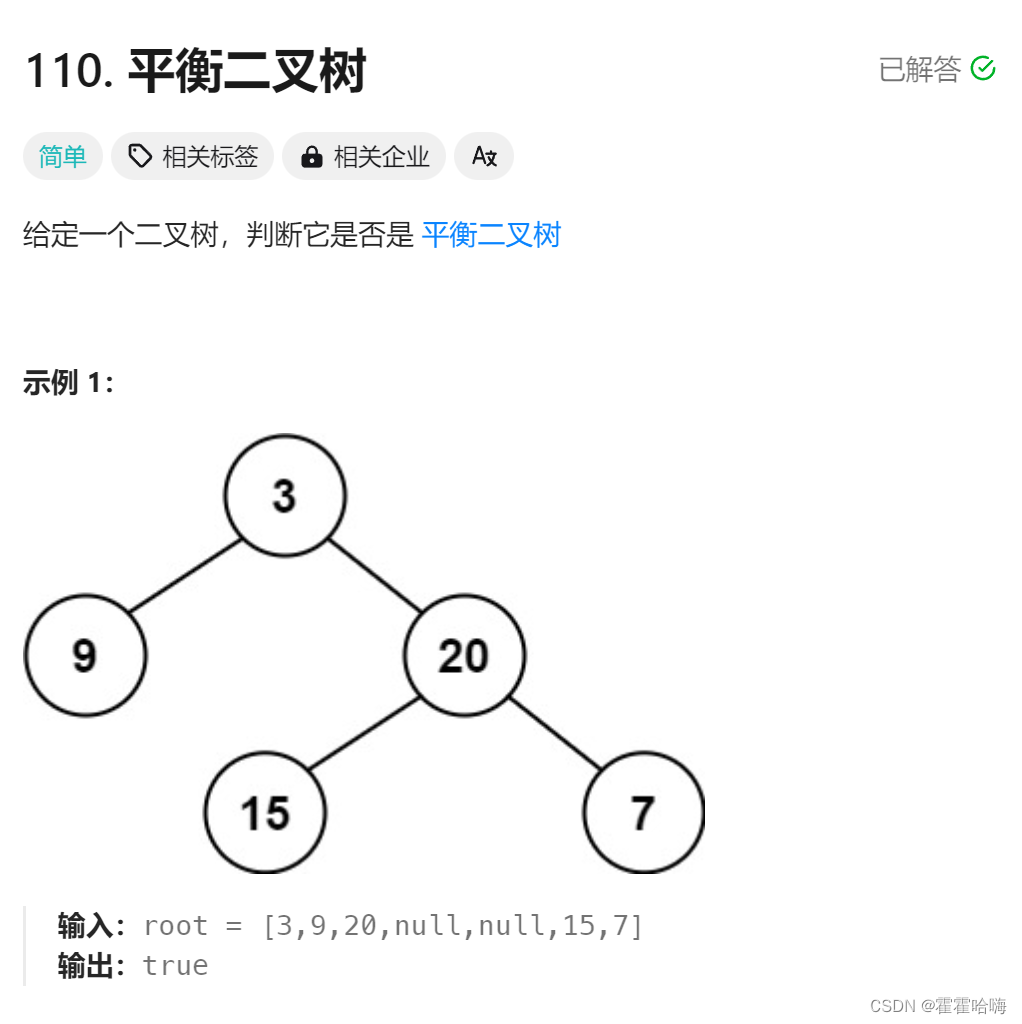
平衡二叉树：是指该树所有节点的左右子树的深度相差不超过 1。

思路：
首先计算出每个节点的左右子树的深度，再计算它们的深度差是否超过1。

代码实现如下：

int maxDepth(struct TreeNode* root) {
    if (root == NULL)
    {
        return 0;
    }

    int leftDepth = maxDepth(root->left);
    int rightDepth = maxDepth(root->right);

    return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}

bool isBalanced(struct TreeNode* root) {
    if (root == NULL)
        return true;

    int leftDepth = maxDepth(root->left);
    int rightDepth = maxDepth(root->right);

    //先检查自己满不满足，再递归检查左子树，右子树满不满足
    return abs(leftDepth - rightDepth) < 2
           && isBalanced(root->left)
           && isBalanced(root->right);
}

4. 二叉树遍历

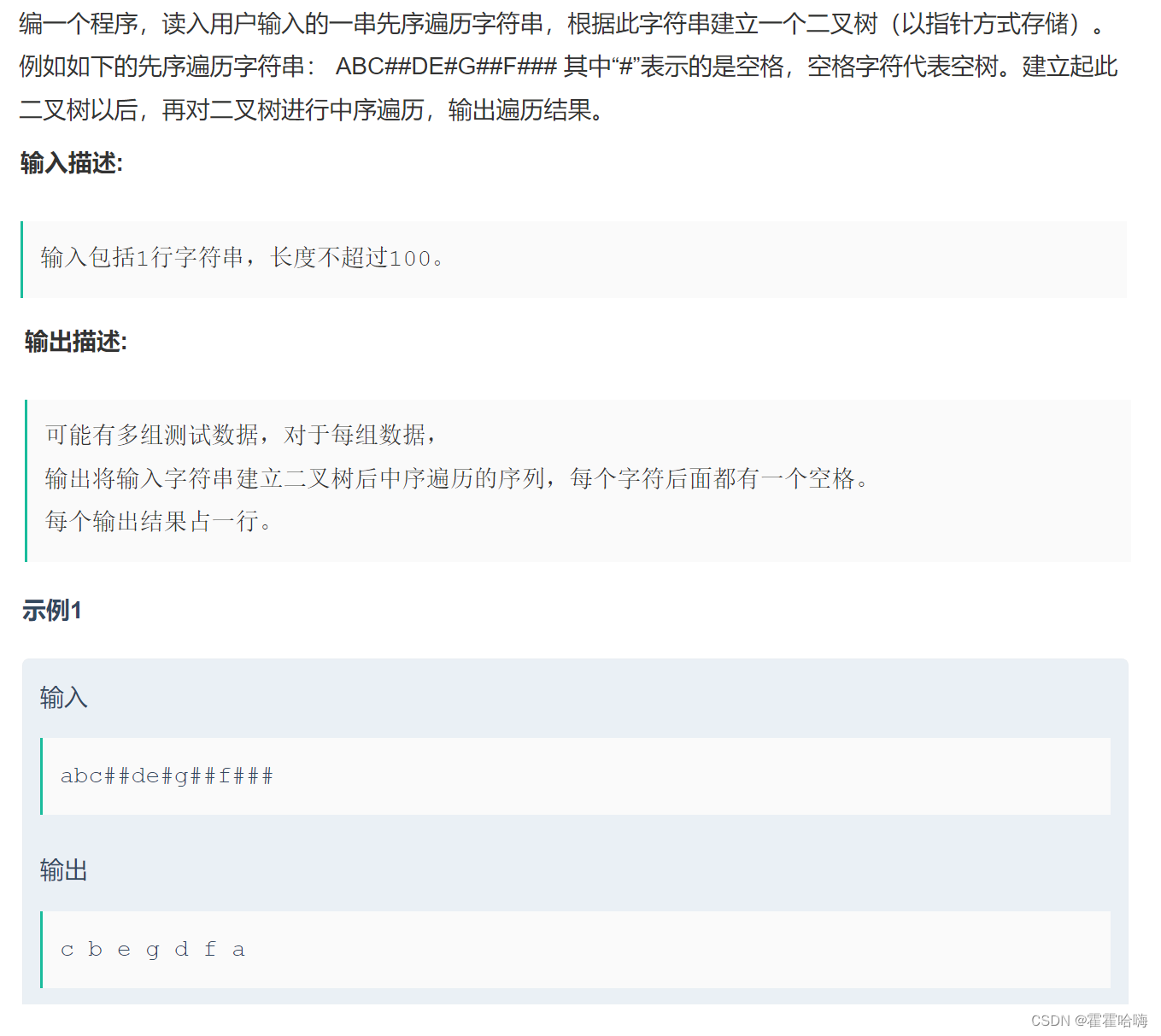
思路：
首先要根据输入的字符串构建一棵二叉树，再进行中序遍历。

代码实现如下：

注意：
局部变量 i 要传地址，不然递归调用时加的不是同一个 i。

//定义结点
typedef struct TreeNode
{
    struct TreeNode* left;
    struct TreeNode* right;
    char val;
}TNode;

//创建二叉树
TNode* CreateTree(char* a, int* pi)
{
    if (a[*pi] == '#')
    {
        (*pi)++;
        return NULL;
    }

    TNode* root = (TNode*)malloc(sizeof(TNode));
    if (root == NULL)
    {
        perror("malloc fail!\n");
        exit(-1);
    }

    root->val = a[*pi];
    (*pi)++;

    root->left = CreateTree(a, pi);
    root->right = CreateTree(a, pi);

    return root;
}

void InOrder(TNode* root)
{
    if (root == NULL)
        return;

    InOrder(root->left);
    printf("%c ", root->val);
    InOrder(root->right);
}

int main() {
    char str[100] = { 0 };
    scanf("%s", str);

    int i = 0;

    //构建一棵树
    TNode* root = CreateTree(str, &i);

    InOrder(root);

    return 0;
}