篇接上文，今天要学习的是归并排序以及非比较排序--计数排序。这么励志的日更博主，你怎么能不三连一下呢？
目录
一、归并排序
1. 递归实现
2. 非递归实现
3. 特性总结
二、非比较排序--计数排序
三、排序算法复杂度及稳定性分析
一、归并排序
1. 递归实现
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。 归并排序核心步骤：
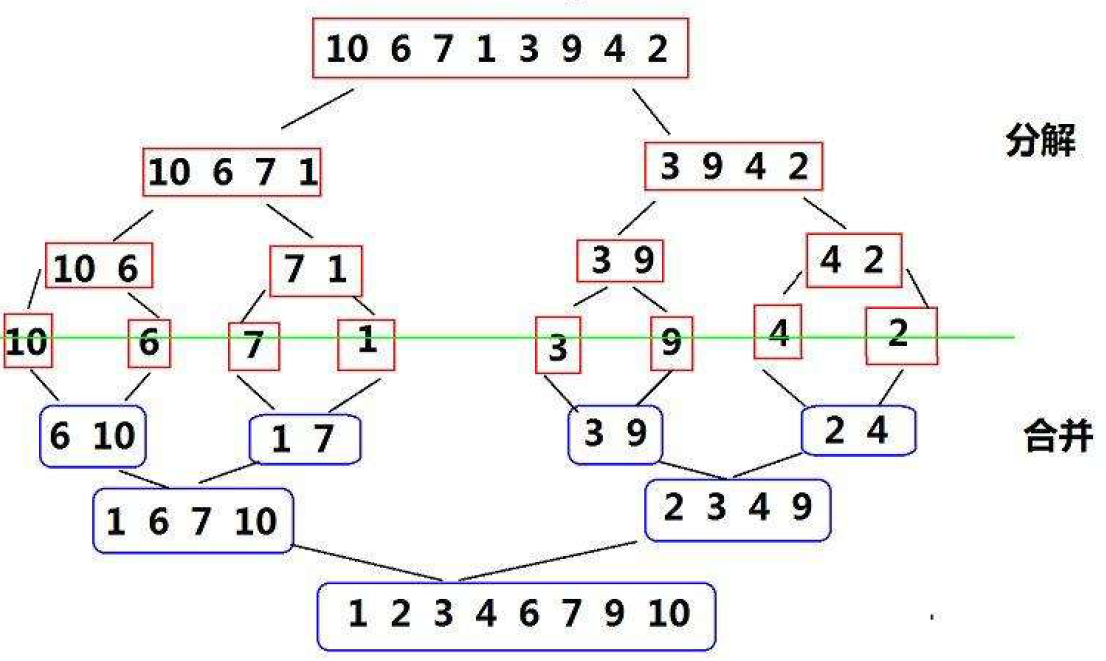
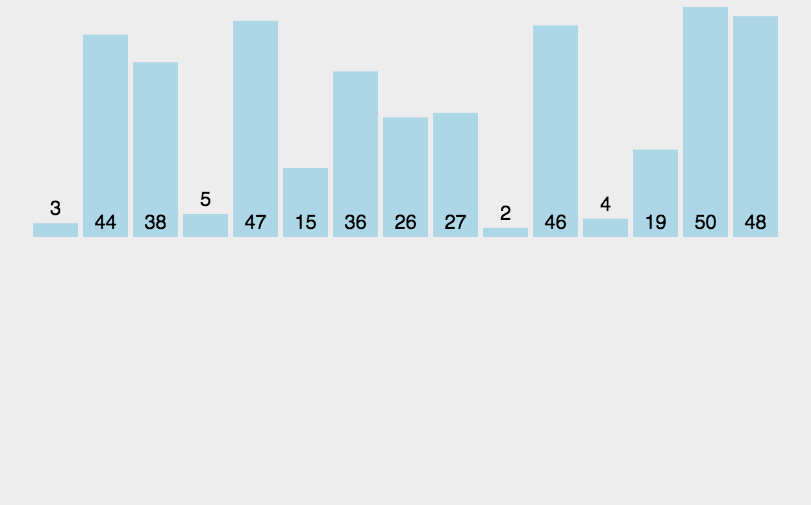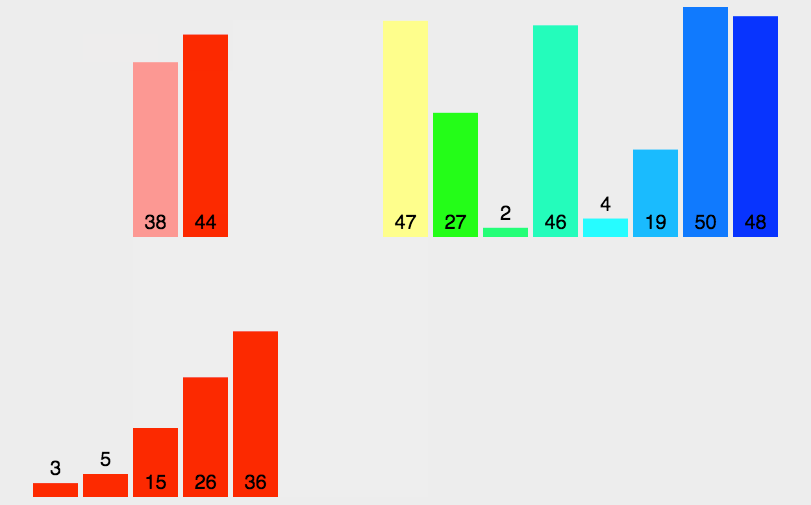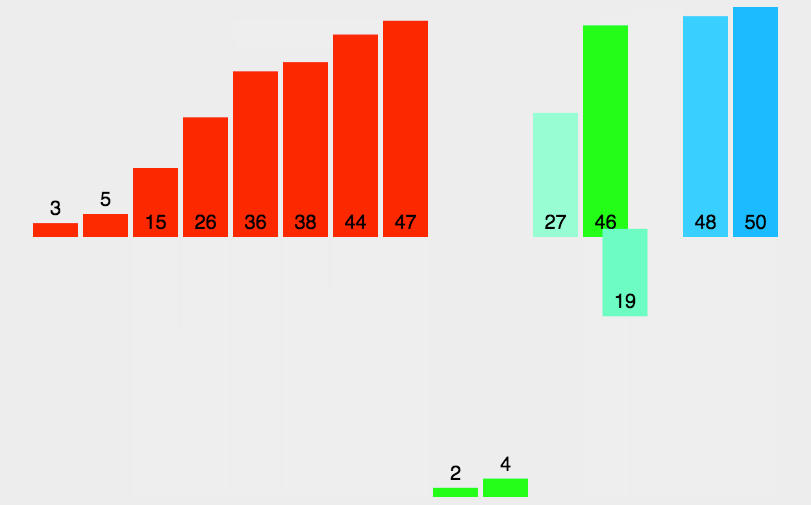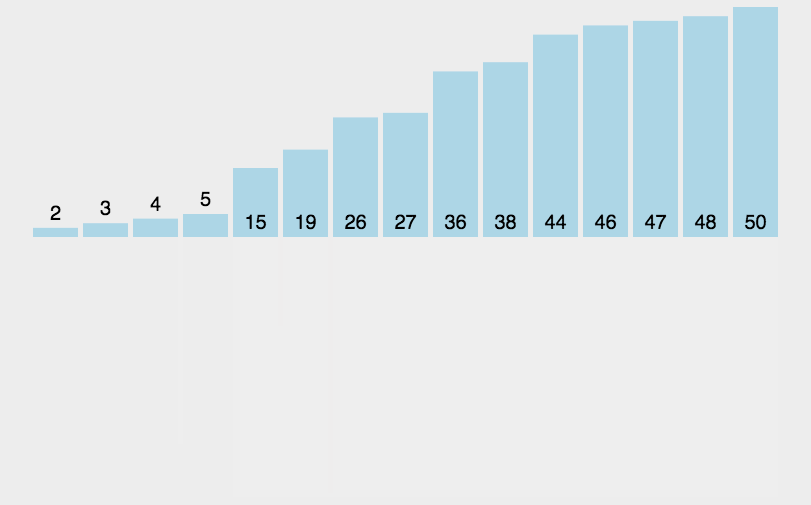
void _MergrSort(int* a, int begin, int end, int* tmp)
{
int mid = (begin + end) / 2;
//将数组分为两部分[begin,mid]和[mid+1,end]
if (begin >= end)
{
return;
}
//分治思想：把不有序的数组拆分成一段段小的数组
//每一段小的数组进行归并排序
_MergrSort(a, begin, mid, tmp);
_MergrSort(a, mid + 1, end, tmp);
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = begin;
//依次比较，取小的尾插到tmp数组里
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);//申请临时数组
if (tmp == NULL)
{
perror("malloc");
return;
}
_MergrSort(a, 0, n - 1, tmp);
free(tmp);
tmp = NULL;
}2. 非递归实现
void MergrSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);//申请临时数组
if (tmp == NULL)
{
perror("malloc");
return;
}
int gap = 1;
while (gap < n)
{
//两组两组归并，因此j每次跳过2个gap
for (int j = 0; j < n; j += 2 * gap)
{
int begin1 = j, end1 = begin1 + gap - 1;
int begin2 = end1 + 1, end2 = begin2 + gap - 1;
int i = j;
//避免存在越界
if (end1 >= n || begin2 >= n)
break;
if (end2 >= n)
end2 = n - 1;
//依次比较，取小的尾插到tmp数组里
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + j, tmp + j, sizeof(int) * (end2 - j + 1));
}
gap *= 2;
}
free(tmp);
tmp = NULL;
}3. 特性总结
- 缺点在于需要
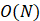的空间复杂度，思考解决在磁盘中的外排序问题。 - 时间复杂度：
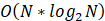
- 空间复杂度：
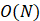
- 稳定性：稳定
二、非比较排序--计数排序
常见的非比较排序：计数排序、基数排序、桶排序。其中需要重点掌握计数排序。
计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用。 操作步骤：
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列中
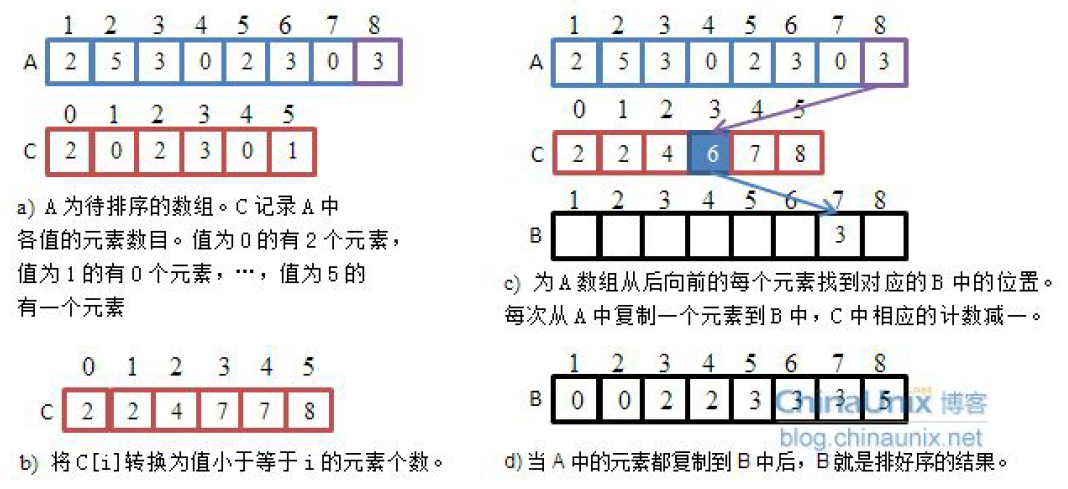
void CountSort(int* a, int n)
{
//找到最大和最小元素，确定数据范围
int min = a[0], max = a[0];
for (int i = 1; i < n; i++)
{
if (a[i] > max)
max = a[i];
if (a[i] < min)
min = a[i];
}
int range = max - min + 1;
//创建大小为range的数组，并把整个数组初始化为0
int* count = (int*)malloc(sizeof(int) * range);
if (count == NULL)
{
perror("malloc");
return;
}
memset(count, 0, sizeof(int) * range);
//统计每个数据出现次数
//min作为count数组的首元素
//通过a[i] - min计算出a[i]在count数组中的下标
for (int i = 0; i < n; i++)
{
count[a[i] - min]++;
}
//min=a[0]，i + min=a[i]
//遍历count数组，进行排序
int j = 0;
for (int i = 0; i < range; i++)
{
while (count[i]--)
{
a[j++] = i + min;
}
}
}特性总结
- 计数排序适合数据集中的数组排序，效率比较高。
- 时间复杂度：
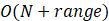
- 空间复杂度：
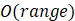
- 稳定性：稳定
- 局限性：只适合整型数据的排序
三、排序算法复杂度及稳定性分析
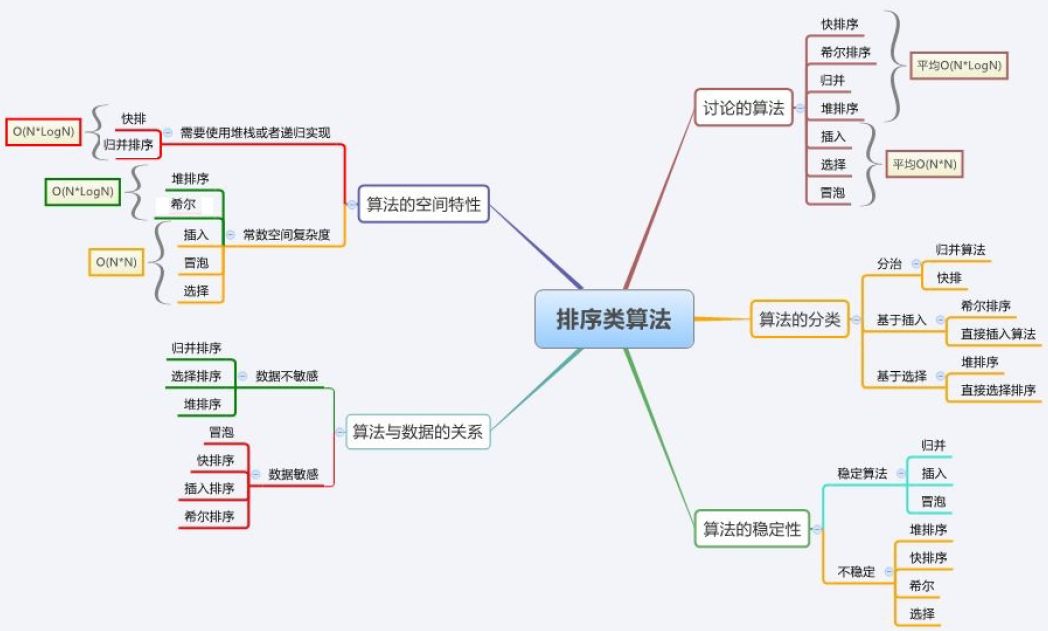
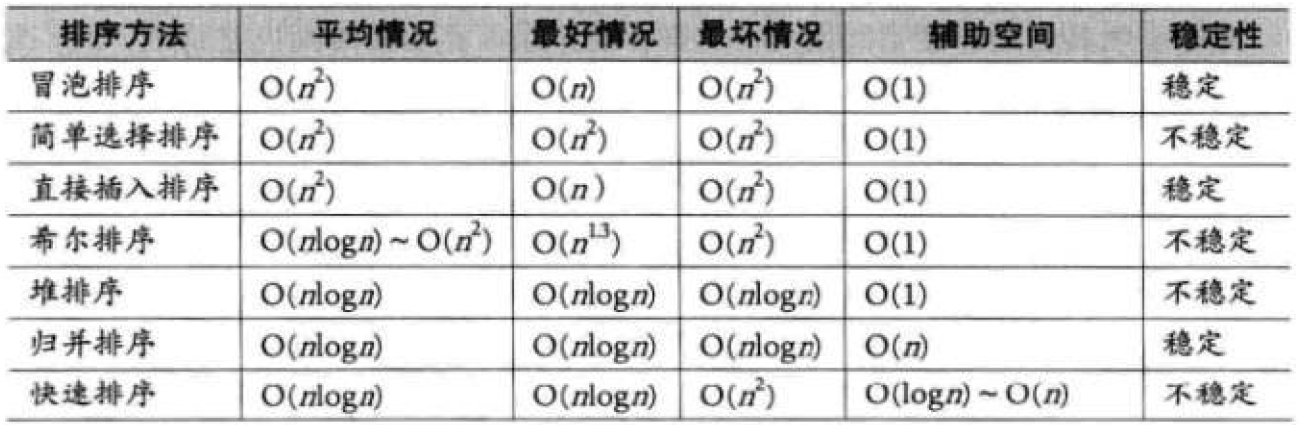
以上便是我们比较常用的排序算法，下一篇我们还会额外给大家介绍一种排序算法--外排序。想了解的话，还不速速三连？？？
