排序的概念及其运用
排序的概念
排序 :所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。稳定性 :假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中, r[i]=r[j] ,且 r[i] 在 r[j] 之前,而在排序后的序列中, r[i] 仍在 r[j] 之前,则称这种排序算法是稳定的;否则称为不稳定的。内部排序 :数据元素全部放在内存中的排序。外部排序 :数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
排序的运用
常见的排序

插入排序:直接插入排序
先写直接插入排序。
直接插入排序是一种简单的插入排序法,其基本思想是:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为 止,得到一个新的有序序列 。 实际中我们玩扑克牌时,就用了插入排序的思想
实际中我们玩扑克牌时,就用了插入排序的思想
一下子写排序是不可取的,排序这个部分,先写单趟,后写整体。
就比如说,我有0~end个数据的下标,我想把该数组外的end+1下标的值插入到现有数据。end在哪里我不清楚,这里只是假设,这里单趟的核心思想就是把一个数往前面的有序区间插入。这里的0~end肯定是有序的。注意注意,这里的end是什么我们并不知道。
这里已经有一个有序区间了。然后我把后一个值往前面插入。
2比5小,所以5得往后挪动,但是一挪动就会覆盖2,所以得先把2存起来。将2保存在一个变量中。比5小挪动,end减减,比3小挪动,end减减,比1大,就放到1的后面。假如要插入的不是2了,而是0,那我还是比1小,1往后挪动,我end减减,然后把0插入在end的后面,所以结束条件为end=-1;
总结:无论哪一种情况,都是放在end的后面。
//单趟插入排序
void InsertSort(int* a, int n)
{
int end=0;
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
--end;
}
else
{
break;
}
}
//这里切记end要加1,否则会出问题,因为我们之前移动后,立马end减去1了。
a[end + 1] = tmp;
}上图是完成了一趟了
这个循环有两个出去的条件,一个是你比end对应的值大于或者等于就break跳出,还有end小于0就结束,就是所有的值都比你目标值大,就一直挪动,挪到end等于-1,就将目标值插入到end的后面。这就是一趟走的整体思路。
完成了一趟的数据后,我们就开始写次数来完善程序。
这里我们把end给为0,就想当然把0当成有序,然后继续来走。
所以给的end的其实位置就是0.所以在循环里,这里就给i。
end为0时,即第一个数据有序,end后的数据开始插入,以此类推。
end的结束位置在数组最后位置的前一个。即有n个数据,那么最后一个数据的下标为n-1,再往前就是n-2;
因为这里要经常打印数组,所以这里就写一个相应的函数。
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}分析时间复杂度
写代码时,要对其的思路逻辑清楚一点,否则会出现问题。
一定要学会单趟套整体。
这个直接插入排序的时间复杂度为多少?千万不要说两层循环n的平方。简单排序看层数是没问题的。但是排序这里看循环层数来判断n的平方是不对的。判断时间复杂度要看思想。
这个直接插入排序,逆序的时候,时间复杂度是最坏的。就是第一个数有序,第二个数插入一次,第三个数两次,就是等差数列。就是得全部挪动一遍。所以也就是1~n-1,也就是n的平方。
![]()
呃呃呃,虽然这个程序是n的平方,但是切记看思想来判断。
这是最坏情况,我们再看一下最好情况,即顺序。就是0(n),就是遍历了一遍。或者说接近有序,这个最好情况再顺序有序或者接近有序时成立。
为什么最好是0(n)呢?就是我给你一个数组,你是不知道他是是否有序的。你不知道他是否有序。没有排序可以做到0(1),最快的排序就是接近0(n)的。当然在一些比较局限的场景里可以做到0(n)。常见的排序n*log(n)就是最好的了。
交换排序:冒泡排序
体现素养的小细节:
写个冒泡,呜呜,遇到友人了。
BubbleSort.(命名要规范,否则面试出大问题)。
规范:代码里面不要有拼音,除非没有对应的单词。这个关乎面试官对你的代码素养。
冒泡排序 是一种交换思想,如果前一个大于后一个就交换,这样以来,一轮之后,最大的值就到最后了。然后再前一个根后一个交换,把次大的值换到倒数第二个位置了。
我们还按照先写单趟,再写整体。
这里先写一个交换函数,因为之后可以复用。
//单趟冒泡排序
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void BubbleSort(int* a, int n)
{
for (int i = 1; i < n; i++)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
}
}
}代码比的是细节。要控制住细节。如果你觉得细节控制的不是太好,那一定是画图画少了。
这里for循环条件也可以给i为0,这样接得写i<n-1了,这样得控制尾部的结束条件了。当然,怎么写都是可以的。
我们这样写的就是一前一后进行交换。
到这里第一次记冒好了,第一次就确定了最大值,所以第二趟就冒到n-1就行了。当<1时,冒泡就结束。所以一共冒泡n-1次就行。
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void BubbleSort(int* a, int n)
{
for (int j = 0; j < n - 1; j++)
{
for (int i = 1; i < n; i++)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
}
}
}
}这里第一层次数循环是到n-2结束,第二层for循环进行每一次需要的趟数到小于n-(n-2)结束,即小于2就结束,也就是到1,我们分析就是到1就继续,正好0和1那里比较了,然后就结束,思路是这样的。
到这里,冒泡就写好了,但是其实还是可以优化的。
冒泡空间有可优化的空间,就是顺序可能或者基本有序,就不冒一趟没有发现数据交换,就不用再继续走了,这里给个标志。
void BubbleSort(int* a, int n)
{
for (int j = 0; j < n - 1; j++)
{
int exchange = 0;
for (int i = 1; i < n; i++)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}冒泡排序的时间复杂度是n的平方。这个时候的最坏的情况不是说逆序了,逆序只是其中一种情况,不一定是逆序,很多情况都是n的平方。最好的顺序就是接近有序从而达到0(n)。
它和插入排序看起来没什么区别,但其实不一样。
冒泡排序的特性总结:1. 冒泡排序是一种非常容易理解的排序2. 时间复杂度: O(N^2)3. 空间复杂度: O(1)4. 稳定性:稳定
对比直接插入排序和冒泡排序
// 测试排序的性能对比
void TestOP()
{
srand(time(0));
//开100000个空间
const int N = 100000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
int* a6 = (int*)malloc(sizeof(int) * N);
//每个数组放一样的数
for (int i = 0; i < N; ++i)
{
a1[i] = rand();
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
}
//计算时间
int begin1 = clock();
InsertSort(a1, N);
int end1 = clock();
int begin2 = clock();
BubbleSort(a2, N);
int end2 = clock();
/*int begin3 = clock();
SelectSort(a3, N);
int end3 = clock();
int begin4 = clock();
HeapSort(a4, N);
int end4 = clock();
int begin5 = clock();
QuickSort(a5, 0, N - 1);
int end5 = clock();
int begin6 = clock();
MergeSort(a6, N);
int end6 = clock();*/
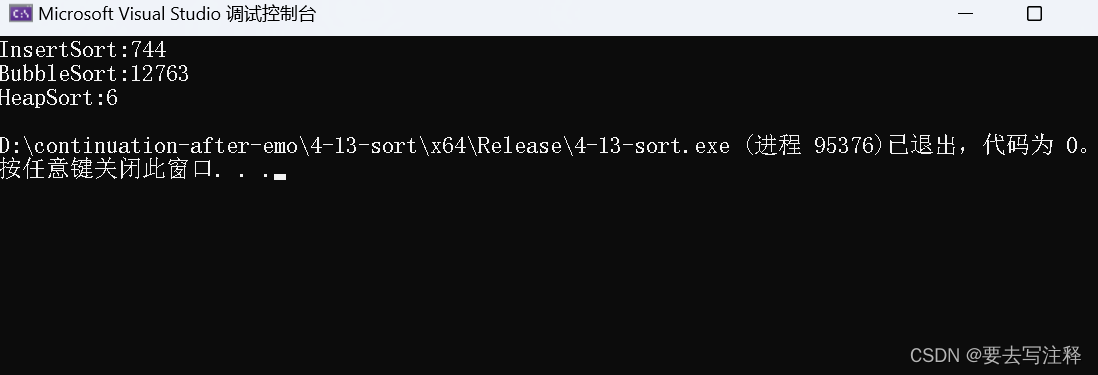
printf("InsertSort:%d\n", end1 - begin1);
printf("BubbleSort:%d\n", end2 - begin2);
/*printf("SelectSort:%d\n", end3 - begin3);
printf("HeapSort:%d\n", end4 - begin4);
printf("QuickSort:%d\n", end5 - begin5);
printf("MergeSort:%d\n", end6 - begin6);*/
free(a1);
free(a2);
/*free(a3);
free(a4);
free(a5);
free(a6);*/
}
int main()
{
/*int a[] = { 5,4,3,2,1 };
BubbleSort(a, sizeof(a) / sizeof(a[0]));
PrintArray(a, sizeof(a) / sizeof(a[0]));*/
TestOP();
return 0;
}malloc个多个数组,产生一个随机值。然后将数组1赋值给别的数组,就是说这6个数组的值都是一样的。
这里begin减去end就是排序所消耗的时间。
clock是电脑运行启动到调用这个函数是所消耗的毫秒数,所以两个clock之差就是中间的排序消耗掉的时间。

这里进行测试时,debug可能优化没有全开,测性能用release。
下图是realease的。

跑十万个值进行的比较。
所以明显的感觉到这两个不一样。不能单看时间复杂度来看这里的问题。
时间复杂度用来算他是属于哪一个量级的。这两个属于同一个档次的排序。同一个学校,是统一档次,但出来的不同同学有不同。
所以不能单一时间复杂度来评估。
选择排序:堆排序
堆排序 (Heapsort) 是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。 需要注意的是排升序要建大堆,排降序建小堆。

1. 堆排序使用堆来选数,效率就高了很多。2. 时间复杂度: O(N*logN)3. 空间复杂度: O(1)4. 稳定性:不稳定
void HeapSort(int* a, int n)
{
//a数组直接建堆 0(N)
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(a, n, i);
}
//O(N*logN)
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
printf("%d ", a[end]);
--end;
}
printf("%d", a[0]);
}
int main()
{
int a[] = { 5,4,3,2,1 };
HeapSort(a, sizeof(a) / sizeof(a[0]));
//PrintArray(a, sizeof(a) / sizeof(a[0]));
//TestOP();
return 0;
}
排序和排序直接真的有差距啊。
插入和冒泡属于同一类,但效率差很多的重要的点在,插入具有很强的适应性。
冒泡不再冒的条件是很苛刻的,就是不能有任何一个交换,没有一个条件交换,就是已经有序了,这个条件是很难达成的。
插入的适应性在哪里呢?只要由一个靠后的数据比前面数据都小,那就挪动n次。但是这是非常极端的,一般来说这个数据可能在偏中间一点的位置,即只挪动了一半的数据就达到了目的。

这个堆冒泡是常态,但对于插入排序来说,他只要每个数据都要挪满时才会出现这种情况。但是对插入排序来说,他的中间或许可能会局部有序,他不需要;一直挪。随机的场景更多的是局部有序。
时间复杂度不在同一个量级就没有可比性,在同一个量级的也有差异。冒泡在随机数是都是比满。
插入排序:希尔排序
希尔觉得插入排序非常的不错,如果有序接近有序,插入有序就非常nb了。它要改革直接插入排序。如果能把数据接近有序,那就很快乐。
所以他分为两个步骤:
预排序 目标:接近有序;
他觉得你挪动的太慢了。它想让挪动的快一些。也就是分组插入排序。目标:大的更快换到后面的位置,小的数更快换到前面的位置。
就是以gap为间距来一一分组。
希尔排序法又称缩小增量法。希尔排序法的基本思想是: 先选定一个整数,把待排序文件中所有记录分成个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达 =1 时,所有记录在统一组内排好序 。

希尔排序的特性总结:1. 希尔排序是对直接插入排序的优化。2. 当 gap > 1 时都是预排序,目的是让数组更接近于有序。当 gap == 1 时,数组已经接近有序的了,这样就 会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。3. 希尔排序的时间复杂度不好计算,因为 gap 的取值方法很多,导致很难去计算,因此在好些树中给出的 希尔排序的时间复杂度都不固定
《数据结构(C语言版)》--- 严蔚敏

《数据结构-用面相对象方法与C++描述》--- 殷人昆

稳定性:不稳定


预排序和原数组相比:

他有序了一点,但不是很多。
我们先写单趟。
我们接下来以下图这个数组为例开始排

//单次希尔排序
void ShellSort(int* a, int n)
{
int gap = 3;
int end=0;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}比完5和2了,然后比5和3时,不是上述代码,写的,得先在上图再套一层才能写,这里先继续写。
这里跟插入排序很像,无非就是将加1换成了加gap。
刚才完成的只是把一个数往前插入,如果我们要排一组数据,那么该如何排。
for(int i=0;i<n;i+=gap)
上图这里再套一层循环。但是这里有问题,如果i等于在5的位置时(即进行了交换之后),再加上gap来进入循环,这个时候就越界了。

所以外层循环应该写为上图:
这个时候就帮助我们帮红色这一组就排完了,但是我们想排整体,该如何呢?间距为gap,就有gap组。gap是几就有几组。所以再次套一层循环。
//一个gap进行的希尔排序
void ShellSort(int* a, int n)
{
int gap = 3;
for (int i = 0; i < n-gap; i += gap)
{
int end=i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}所以外层循环应该写为上图:
这个时候就帮助我们帮红色这一组就排完了,但是我们想排整体,该如何呢?间距为gap,就有gap组。gap是几就有几组。所以再次套一层循环。
//完整的希尔排序
void ShellSort(int* a, int n)
{
int gap = 3;
for (int j = 0; j < gap; j++)
{
for (int i = 0; i < n - gap; i += gap)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}总结一下:希尔排序分为预排序他的目的是分组插入排序
预排序的目标是:大的更快换到后面的位置,小的数更快换到前面的位置。
到这里,其实上图完整的希尔排序也可以简化为2层。
void ShellSort(int* a, int n)
{
int gap = 3;
/*for (int j = 0; j < gap; j++)
{
for (int i = 0; i < n - gap; i += gap)
{*/
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
/* }
}*/
}
希尔排序是初始的是什么呢,是一组排完排另一组。是排完红色,再排绿色,再排紫色。
一组一组排。
但是按照上图来说,先比较换了2和5,然后不一整组一整组比较,而是最外层的i++。这个方法是gap组数据,交替完成分组插入排序。
gap大于1就是预排,等于1就是快速排序。gap越大,数据跳的越快,大的更快到前面为止,小的更快到后面,但是越不接近有序。
gap越小,数据跳的越慢,但是越接近有序,gap==1就是插入后就是有序。
继续深入;
这里还有人怎么给呢?到这里就已经变为怎么给gap了。

这样就能控制gap了,我第一次间距给上50,gap大不接近有序,没关系啊,我gap在缩小,我除以2最后一趟一定是1.

这里希尔排序每一组都在接近有序。
呜呜呜呜,开始这个排序让你爱答不理,最后让我高攀不起。呜呜呜呜!
有人觉得除3更好,但是除3不能保证最后余数为1.
代码能力是练出来的。需要消化的数据才是有含量的。
若有收获,就点个赞吧