目录
#A 空间
#B 卡片
#C 直线
#D 货物摆放
#E 路径
#F 时间显示
#G 砝码称重
#H 杨辉三角形
#I 双向排序
#J 括号序列
#A 空间

#include <bits/stdc++.h>
using namespace std;
int main()
{
cout<<256 * 1024 * 1024 / 4<<endl;
return 0;
}#B 卡片

#include <bits/stdc++.h>
using namespace std;
//存储0-9
int arr[10];
bool merge(int n)
{
//数字n能否被拼成
while(n > 0)
{
if(--arr[n%10] < 0) return false;
n /= 10;
}
return true;
}
int main()
{
for(int i = 0;i < 10;i++)
arr[i] = 2021;
//遍历
for(int i = 1;i < 1000000;i++)
if(!merge(i))
{
cout<<i-1<<endl;
break;
}
return 0;
}#C 直线

#include <bits/stdc++.h>
using namespace std;
const int X = 20, Y = 21;
int link[X][Y][X][Y], ans;
int main()
{
for(int x1 = 0;x1 < X;x1++)
{
for(int y1 = 0;y1 < Y;y1++)
{
link[x1][y1][x1][y1] = 1;
for(int x2 = 0;x2 < X;x2++)
{
for(int y2 = 0;y2 < Y;y2++)
{
// (x1,y1)->(x2,y2)
if(!link[x1][y1][x2][y2])
{
int x = x1;
int x_offset = x1 - x2;
int y = y1;
int y_offset = y1 - y2;
while(x >= 0 && x < X && y >= 0 && y < Y)
{
x -= x_offset;
y -= y_offset;
}
//所有加上偏移量的点都会被访问,全部剔除
for(x += x_offset,y += y_offset; x >= 0 && x < X && y >= 0 && y < Y;x += x_offset,y += y_offset)
{
for(int xx = x,yy = y;xx >= 0 && xx < X && yy >= 0 && yy < Y;xx += x_offset,yy += y_offset)
{
link[x][y][xx][yy] = link[xx][yy][x][y] = 1;
}
}
ans++;
}
}
}
}
}
cout<<ans<<endl;
return 0;
}#D 货物摆放

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll N = 2021041820210418;
ll ans = 0;
int main()
{
set<ll> sets;
//2021041820210418
//求这个数字的全部因子
for(ll i = 1;i * i <= N;i++)
{
if(N % i == 0)
{
sets.insert(i);
sets.insert(N / i);
}
}
//遍历因子
for(set<ll>::iterator i = sets.begin(); i != sets.end();i++)
{
for(set<ll>::iterator j = sets.begin(); j != sets.end();j++)
{
for(set<ll>::iterator k = sets.begin(); k != sets.end();k++)
if(*i * *j * *k == N) ans++;
}
}
cout<<ans<<endl;
return 0;
}#E 路径

#include <bits/stdc++.h>
using namespace std;
const int n = 2021;
int metric[n+1][n+1];
int gcd(int a,int b)
{
if(a % b == 0) return b;
return gcd(b, a % b);
}
int lcm(int a,int b)
{
return a * b / gcd(a,b);
}
int main()
{
//每条边都给最大值
for(int i = 0;i <= n;i++)
for(int j = 0;j <= n;j++)
metric[i][j] = 99999999;
//计算结点之间的长度
for(int a = 1;a <= n;a++)
{
for(int b = min(n,a+21);b > a;b--)
metric[a][b] = metric[b][a] = lcm(a,b);
}
//弗洛伊德算法
for(int k = 1;k <= n;k++)
for(int i = 1;i <= n;i++)
for(int j = 1;j <= n;j++)
metric[i][j] = min(metric[i][j], metric[i][k] + metric[k][j]);
cout<<metric[1][n]<<endl;
return 0;
}#F 时间显示

测试样例1
Input:
46800999
Output:
13:00:00
测试样例2
Input:
1618708103123
Output:
01:08:23
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
ll n,second,minutes,hour;
cin>>n;
//时 分 秒
n /= 1000;
hour = (n / 60 / 60) % 24;
minutes = (n / 60) % 60;
second = n % 60;
if(hour < 10) cout<<"0";
cout<<hour<<":";
if(minutes < 10) cout<<"0";
cout<<minutes<<":";
if(second < 10) cout<<"0";
cout<<second;
return 0;
}#G 砝码称重

测试样例1
Input:
3
1 4 6
Output:
10
Explanation:
能称出的 10 种重量是:1、2、3、4、5、6、7、9、10、11。
1 = 1;
2 = 6 − 4 (天平一边放 6,另一边放 4);
3 = 4 − 1;
4 = 4;
5 = 6 − 1;
6 = 6;
7 = 1 + 6;
9 = 4 + 6 − 1;
10 = 4 + 6;
11 = 1 + 4 + 6。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100000+1;
/*
定义一个二维数组,分为两行
第一行用来存储可以被称出的重量,第j列表示的就是重量j
第二行用来临时存放称出的重量,作为重量的中转站
dp[i][j] == true时,表示重量j可以被称出
dp[i][j] == false时,表示重量j不能被称出
*/
bool dp[2][N];
int main()
{
int n,w,sum = 0;
cin>>n;
for(int i = 0;i < n;i++)
{
cin>>w;
sum += w;
//从重量1开始计算
for(int j = 1;j <= sum;j++)
{
if(dp[0][j])
{
dp[1][abs(w-j)] = true;
dp[1][w+j] = true;
}
}
//将第二行数据移动到第一行
for(int j = 1;j <= sum;j++)
{
if(dp[1][j]) dp[0][j] = true;
}
//当前砝码可以被称出
dp[0][w] = true;
}
int ans = 0;
for(int i = 0;i <= sum;i++)
if(dp[0][i]) ans++;
cout<<ans<<endl;
return 0;
}#H 杨辉三角形


测试样例1
Input:
6
Output:
13
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll arr[45000];
int main()
{
ll n;
cin>>n;
if(n == 1)
{
cout<<1<<endl;
return 0;
}
arr[0] = 1;
ll count = 1;
//从第二行开始
for(int i = 1;i < 45000;i++)
{
//从右向左移动
for(int j = i;j > 0;j--)
{
arr[j] += arr[j-1];
if(arr[j] == n)
{
count += i - j + 1;
cout<<count<<endl;
return 0;
}
}
count += (i + 1);
}
//如果某一行的第三列数值已经大于10亿了,说明在这之前都没有对应的数字,这个数字就只能出现在第二列中了
//递增数列求和即可
cout<<(1 + n)*n / 2 + 2<<endl;
return 0;
}#I 双向排序

测试样例1
Input:
3 3
0 3
1 2
0 2
Output:
3 1 2
Explanation:
原数列为 (1, 2, 3)。
第 1 步后为 (3, 2, 1)。
第 2 步后为 (3, 1, 2)。
第 3 步后为 (3, 1, 2)。与第 2 步操作后相同,因为前两个数已经是降序了。
#include <bits/stdc++.h>
using namespace std;
const int N = 100000;
int arr[N];
int main()
{
int n,m,p,q;
cin >>n>>m;
for(int i = 0;i < n;i++)
arr[i] = i + 1;
for(int i = 0;i < m;i++)
{
cin>>p>>q;
if(p == 1)
{
sort(arr+q-1,arr+n,less<int>());
}
else
{
sort(arr,arr+q,greater<int>());
}
}
for(int i = 0;i < n;i++)
cout<<arr[i]<<" ";
return 0;
}#J 括号序列
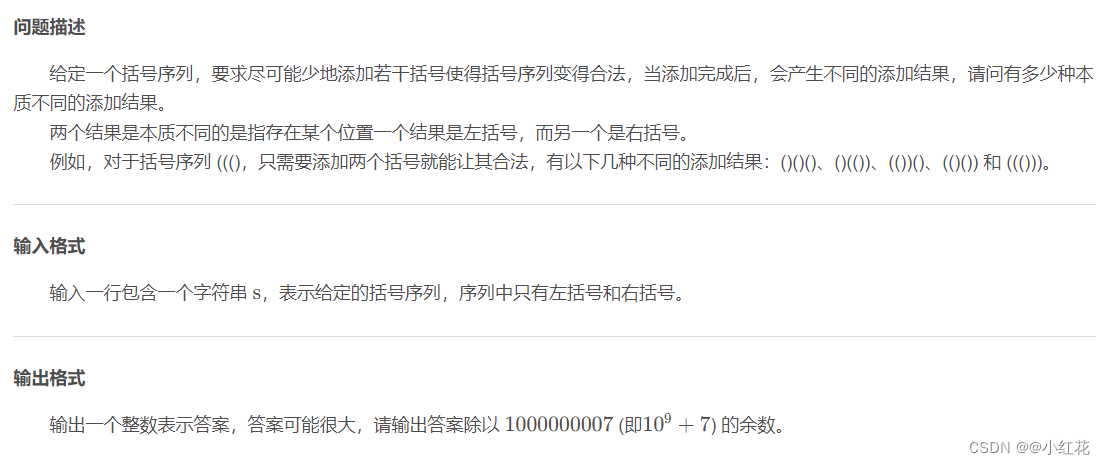
测试样例1
Input:
((()
Output:
5
不会