图解二叉树遍历方法-前序遍历、中序遍历、后序遍历

news2025/6/21 18:27:13

一、几个概念

二叉树（binary tree）：是 n（n >= 0）个结点（每个结点最多只有2棵子树）的有限集合，该集合可为空集（称为空二叉树），或由一个根节点和两颗互不相交的，称为根节点的左子树和右子树的二叉树组成。

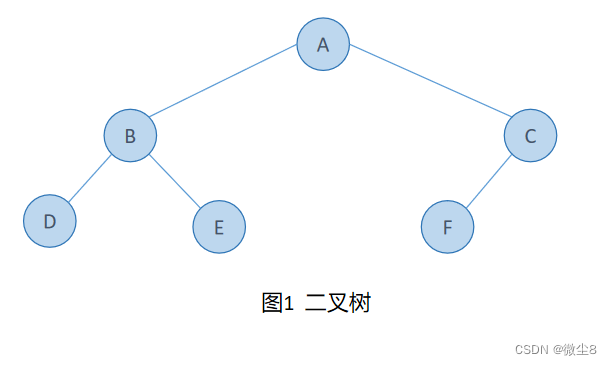
如下图中

图1是一棵二叉树。

图2是非二叉树，因为 A 结点有3棵子树，其次 E 结点和 F 结点相交了

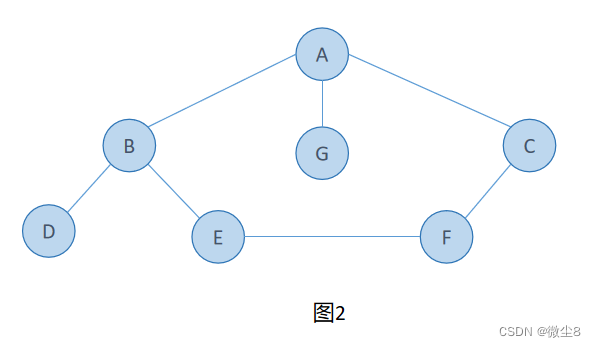
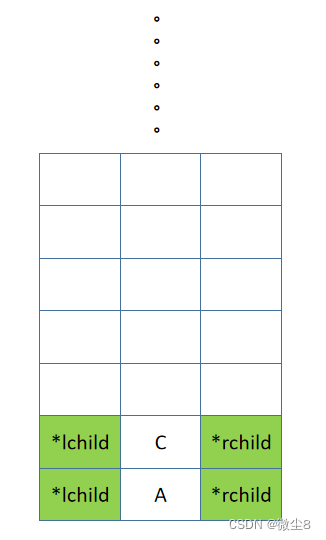
二叉链表：是二叉树的一种链式存储结构，其中每个结点包含三个字段：一个数据字段(data)和两个指针字段(*lchild、*rchild)，分别指向该结点的左孩子和右孩子。如果某个结点没有左孩子或右孩子，那么对应的指针字段为NULL。

用 C 语言可以表述为：

typedef struct binary_node {
    char data;
    struct binary_node *lchild, *rchild;
}binary_tree;

二、前序遍历二叉树（Pre-order Traversal）

        前序遍历二叉树（Pre-order Traversal）的规则为：从根结点出发，先访问该结点，然后前序遍历该结点的左子树，再然后前序遍历该结点的右子树

所以，前序遍历图1这棵二叉树的步骤如图4所示

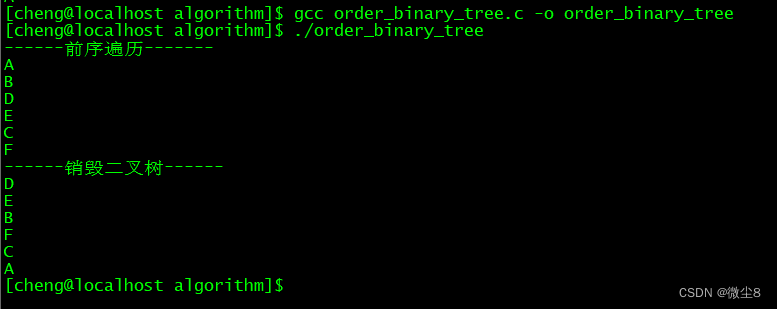
所以，图1这颗二叉树的前序遍历顺序为：ABDECF

1、算法思路

（1）从根结点 A 出发，A 结点入栈，先访问 A 结点，然后前序遍历 A 结点的左子树

（2）A 结点的左子树的根结点为 B，B 结点入栈，先访问 B 结点，然后前序遍历 B 结点的左子树

（3）B 结点的左子树的根结点为 D，D 结点入栈，先访问 D 结点，然后前序遍历 D 结点的左子树

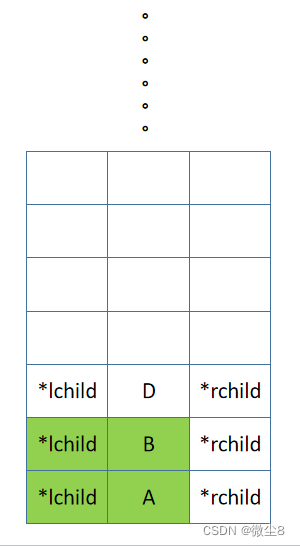
（4）D 结点的左子树为空，则返回

（5）逻辑返回到 D 结点，然后前序遍历 D 结点的右子树

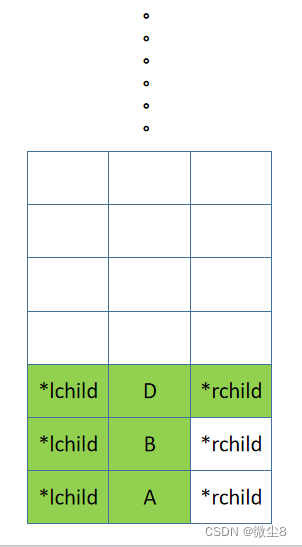
（6）D 结点的右子树为空，则返回

（7）逻辑返回到 D 结点，此时访问 D 结点，前序遍历 D 结点的左右子树的逻辑都已完成，则返回，D 结点出栈。

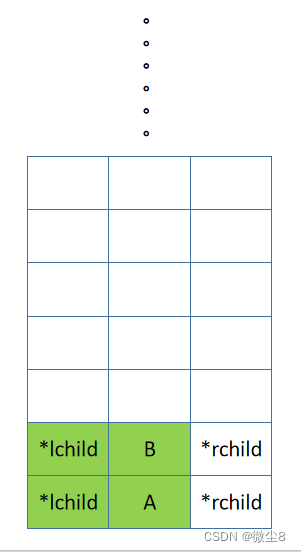
（8）逻辑返回到 B 结点，然后前序遍历 B 结点的右子树

（9）B 结点的右子树的根结点为 E，E 结点入栈，先访问 E 结点，然后前序遍历 E 结点的左子树

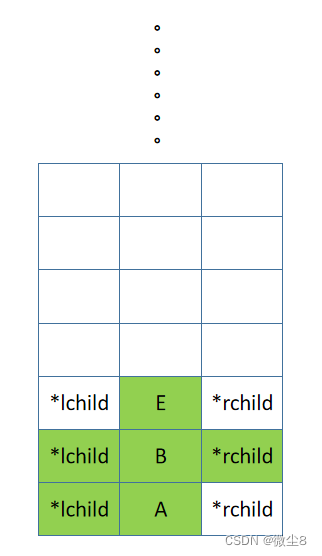
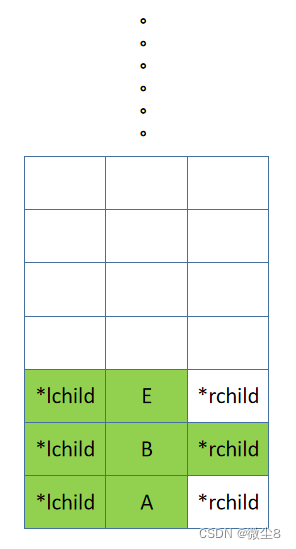
（10）E 结点的左子树为空，则返回

（11）逻辑返回到 E 结点，然后前序遍历 E 结点的右子树

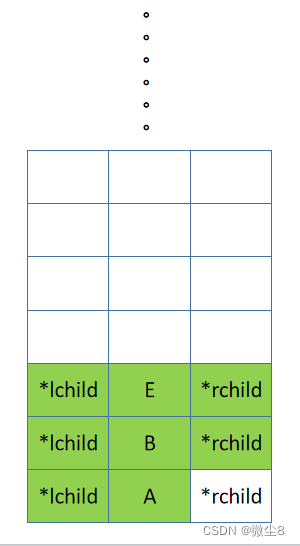
（12）E 结点的右子树为空，则返回

（13）逻辑返回到 E 结点，此时访问 E 结点，前序遍历 E 结点的左右子树的逻辑都已完成，则返回，E 结点出栈。

（14）逻辑返回到 B 结点，此时访问 B 结点，前序遍历 B 结点的左右子树的逻辑都已完成，则函数返回，B 结点出栈。

（15）逻辑返回到 A 结点，然后前序遍历 A 结点的右子树

（16）A 结点的右子树的根结点为 C，C 结点入栈，先访问 C 结点，然后前序遍历 C 结点的左子树

（17）C 结点的左子树的根结点为 F，F 结点入栈，先访问 F 结点，然后前序遍历 F 结点的左子树

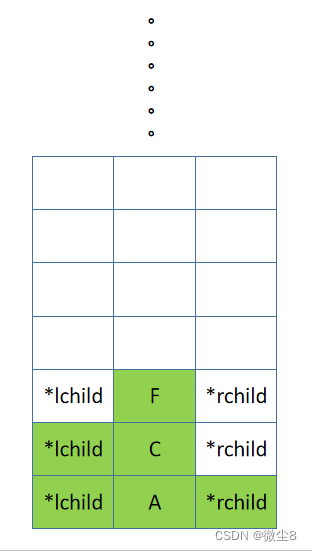
（18）F 结点的左子树为空，则返回

（19）逻辑返回到 F 结点，然后前序遍历 F 结点的右子树

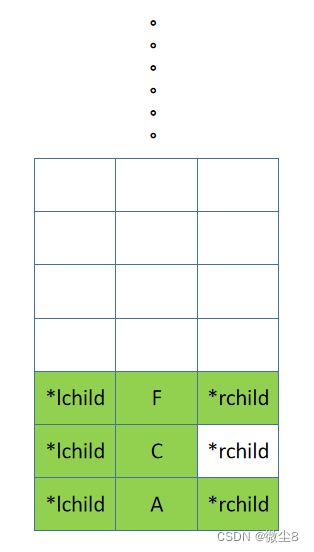
（20）F 结点的右子树为空，则返回

（21）逻辑返回到 F 结点，此时访问 F 结点，前序遍历 F 结点的左右子树的逻辑都已完成，则返回，F 结点出栈。

（22）逻辑返回到 C 结点，然后前序遍历 C 结点的右子树

（23）C 结点的右子树为空，则返回

（24）逻辑返回到 C 结点，此时访问 C 结点，前序遍历 C 结点的左右子树的逻辑都已完成，则返回，C 结点出栈。

（25）逻辑返回到 A 结点，此时访问 A 结点，前序遍历 A 结点的左右子树的逻辑都已完成，则返回，A 结点出栈。

（26）前序遍历二叉树已完成， 所以，前序遍历顺序为：ABDECF

2、实现代码

#include <stdio.h>
#include <string.h>
#include <stdlib.h>

char *g_str = "ABD##E##CF###"; // 扩展二叉树前序序列
int g_index = 0;
typedef struct binary_node {
    char data;
    struct binary_node *lchild, *rchild;
}binary_tree;

void create_binary_tree(binary_tree **T) {
    if (strlen(g_str) == 0)
        return;
    
    if (g_str[g_index] == '#') {
        *T = NULL;
        g_index++;
    } else {
        *T = malloc(sizeof(**T));
        (*T)->data = g_str[g_index];
        g_index++;
        create_binary_tree(&(*T)->lchild);
        create_binary_tree(&(*T)->rchild);
    }
}

void visit_node(binary_tree *T) {
    printf("%c\n", T->data);
}

void pre_order_tree(binary_tree *T) {
    if (!T)
        return;
    
    visit_node(T);
    pre_order_tree(T->lchild);
    pre_order_tree(T->rchild);
}

/*销毁用后序遍历*/
void destroy_binary_tree(binary_tree *T) {
    if (!T)
        return;
    
    destroy_binary_tree(T->lchild);
    destroy_binary_tree(T->rchild);
    printf("%c\n", T->data);
    free(T);
}

int main(int argc, char *argv[]) {
    binary_tree *T;
    create_binary_tree(&T);
    printf("------前序遍历-------\n");
    pre_order_tree(T);
    printf("------销毁二叉树------\n");
    destroy_binary_tree(T);
    return 0;
}

三、中序遍历二叉树（In-order Traversal）

        中序遍历二叉树（In-order Traversal）的规则为：从根结点出发，先中序遍历该结点的左子树，然后访问该结点，再然后中序遍历该结点的右子树

所以，中序遍历图1这棵二叉树的步骤如下图所示

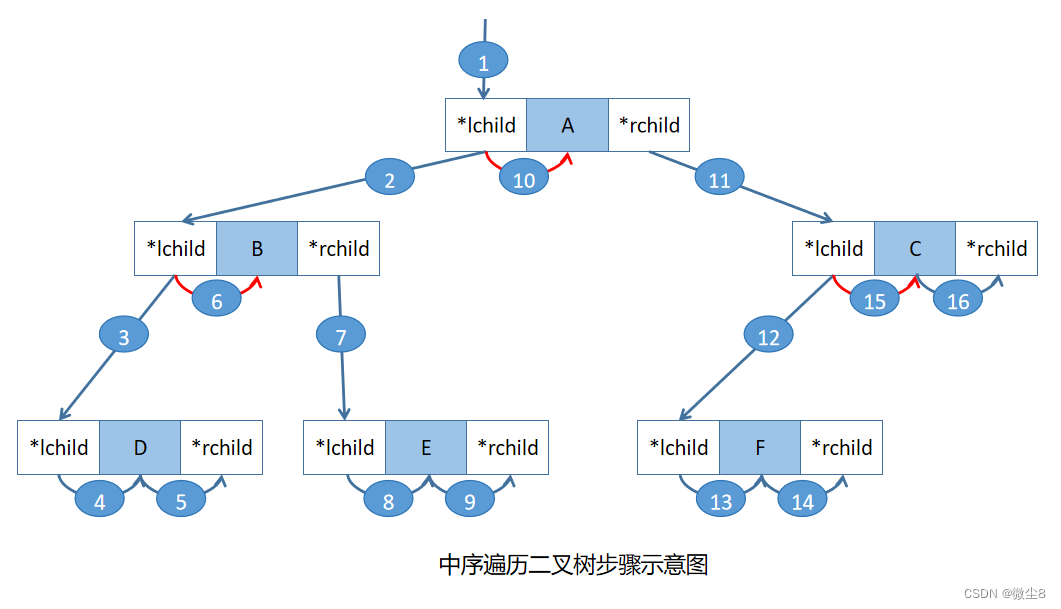
所以，图1这颗二叉树中序遍历顺序为：DBEAFC

1、算法思路

（1）从根结点 A 出发，A 结点入栈，先中序遍历 A 结点的左子树

（2）A 结点的左子树的根结点为 B，B 结点入栈，先中序遍历 B 结点的左子树

（3）B 结点的左子树的根结点为 D，D 结点入栈，先中序遍历 D 结点的左子树

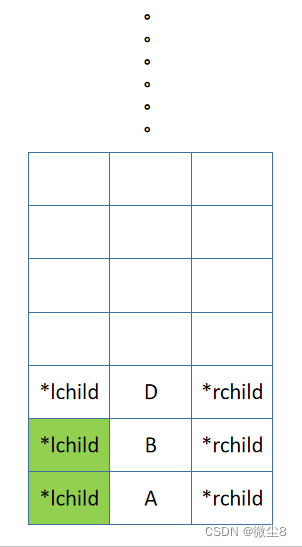
（4）D 结点的左子树为空，则返回

（5）逻辑返回到 D 结点，然后访问 D 结点，再然后中序遍历 D 结点的右子树

（6）D 结点的右子树为空，则返回

（7）逻辑返回到 D 结点，此时中序遍历 D 结点的左子树，访问 D 结点，中序遍历 D 结点的右子树的逻辑都已完成，则返回，D 结点出栈。

（8）逻辑返回到 B 结点，然后访问 B 结点，再然后中序遍历 B 结点的右子树

（9）B 结点的右子树的根结点为 E，E 结点入栈，先中序遍历 E 结点的左子树

（10）E 结点的左子树为空，则返回

（11）逻辑返回到 E 结点，然后访问 E 结点，再然后中序遍历 E 结点的右子树

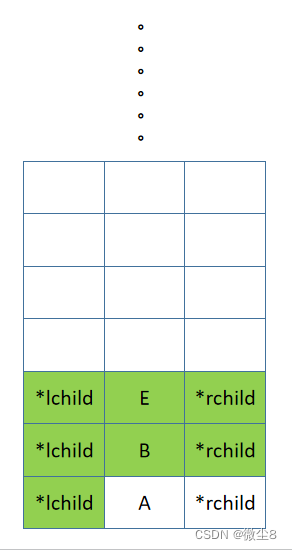
（12）E 结点的右子树为空，则返回

（13）逻辑返回到 E 结点，此时中序遍历 E 结点的左子树，访问 E 结点，中序遍历 E 结点的右子树的逻辑都已完成，则返回，E 结点出栈。

（14）逻辑返回到 B 结点，此时中序遍历 B 结点的左子树，访问 B 结点，中序遍历 B 结点的右子树的逻辑都已完成，则返回，B 结点出栈。

（15）逻辑返回到 A 结点，然后访问 A 结点，再然后中序遍历 A 结点的右子树

（16）A 结点的右子树的根结点为 C，C 结点入栈，先中序遍历 C 结点的左子树

（17）C 结点的左子树的根结点为 F，F 结点入栈，先中序遍历 F 结点的左子树

（18）F 结点的左子树为空，则返回

（19）逻辑返回到 F 结点，然后访问 F 结点，再然后中序遍历 F 结点的右子树

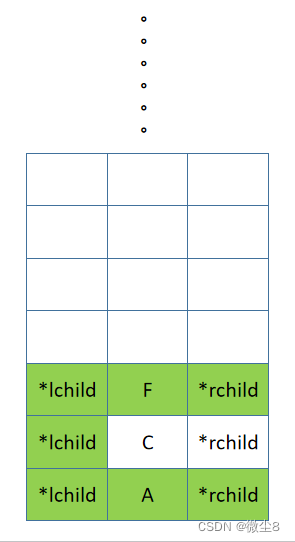
（20）F 结点的右子树为空，则返回

（21）逻辑返回到 F 结点，此时中序遍历 F 结点的左子树，访问 F 结点，中序遍历 F 结点的右子树的逻辑都已完成，则返回，F 结点出栈。

（22）逻辑返回到 C 结点，然后访问 C 结点，再然后中序遍历 C 结点的右子树

（23）C 结点的右子树为空，则返回

（24）逻辑返回到 C 结点，此时中序遍历 C 结点的左子树，访问 C 结点，中序遍历 C 结点的右子树的逻辑都已完成，则返回，C 结点出栈。

（25）逻辑返回到 A 结点，此时中序遍历 A 结点的左子树，访问 A 结点，中序遍历 A 结点的右子树的逻辑都已完成，则返回，A 结点出栈。

（26）中序遍历二叉树已完成， 所以，中序遍历顺序为：DBEAFC

2、实现代码

#include <stdio.h>
#include <string.h>
#include <stdlib.h>

char *g_str = "ABD##E##CF###"; // 扩展二叉树前序序列
int g_index = 0;
typedef struct binary_node {
    char data;
    struct binary_node *lchild, *rchild;
}binary_tree;

void create_binary_tree(binary_tree **T) {
    if (strlen(g_str) == 0)
        return;
    
    if (g_str[g_index] == '#') {
        *T = NULL;
        g_index++;
    } else {
        *T = malloc(sizeof(**T));
        (*T)->data = g_str[g_index];
        g_index++;
        create_binary_tree(&(*T)->lchild);
        create_binary_tree(&(*T)->rchild);
    }
}

void visit_node(binary_tree *T) {
    printf("%c\n", T->data);
}

void pre_order_tree(binary_tree *T) {
    if (!T)
        return;
    
    visit_node(T);
    pre_order_tree(T->lchild);
    pre_order_tree(T->rchild);
}

void in_order_tree(binary_tree *T) {
    if (!T)
        return;
    
    in_order_tree(T->lchild);
    visit_node(T);
    in_order_tree(T->rchild);
}

/*销毁用后序遍历*/
void destroy_binary_tree(binary_tree *T) {
    if (!T)
        return;
    
    destroy_binary_tree(T->lchild);
    destroy_binary_tree(T->rchild);
    printf("%c\n", T->data);
    free(T);
}

int main(int argc, char *argv[]) {
    binary_tree *T;
    create_binary_tree(&T);
    printf("------中序遍历-------\n");
    in_order_tree(T);
    printf("------销毁二叉树------\n");
    destroy_binary_tree(T);
    return 0;
}

四、后序遍历二叉树（Post-order Traversal）

        后序遍历二叉树（Post-order Traversal）的规则为：从根结点出发，先后序遍历该结点的左子树，然后后序遍历该结点的右子树，再然后访问该结点

所以，后序遍历图1这棵二叉树的步骤如下图所示

所以，图1这颗二叉树后序遍历顺序为：DEBFCA

1、算法思路

（1）从根结点 A 出发，A 结点入栈，先后序遍历 A 结点的左子树

（2）A 结点的左子树的根结点为 B，B 结点入栈，先后序遍历 B 结点的左子树

（3）B 结点的左子树的根结点为 D，D 结点入栈，先后序遍历 D 结点的左子树

（4）D 结点的左子树为空，则返回

（5）逻辑返回到 D 结点，然后后序遍历 D 结点的右子树

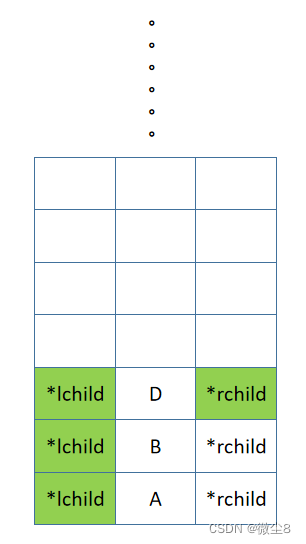
（6）D 结点的右子树为空，则返回

（7）逻辑返回到 D 结点，然后访问 D 结点，此时后序遍历 D 结点的左子树，后序遍历 D 结点的右子树，访问 D 结点的逻辑都已完成，则返回，D 结点出栈。

（8）逻辑返回到 B 结点，然后后序遍历 B 结点的右子树

（9）B 结点的右子树的根结点为 E，E 结点入栈，先后序遍历 E 结点的左子树

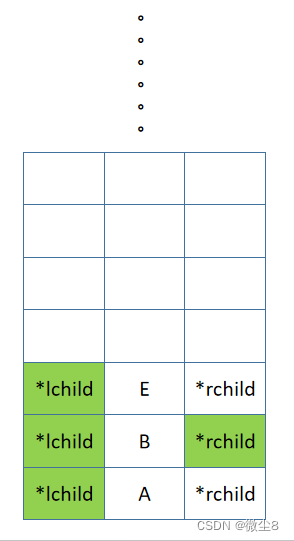
（10）E 结点的左子树为空，则返回

（11）逻辑返回到 E 结点，然后后序遍历 E 结点的右子树

（12）E 结点的右子树为空，则返回

（13）逻辑返回到 E 结点，然后访问 E 结点，此时后序遍历 E 结点的左子树，后序遍历 E 结点的右子树，访问 E 结点的逻辑都已完成，则返回，E 结点出栈。

（14）逻辑返回到 B 结点，然后访问 B 结点，此时后序遍历 B 结点的左子树，后序遍历 B 结点的右子树，访问 B 结点的逻辑都已完成，则返回，B 结点出栈。

（15）逻辑返回到 A 结点，然后后序遍历 A 结点的右子树

（16）A 结点的右子树的根结点为 C，C 结点入栈，先后序遍历 C 结点的左子树

（17）C 结点的左子树的根结点为 F，F 结点入栈，先后序遍历 F 结点的左子树

（18）F 结点的左子树为空，则返回

（19）逻辑返回到 F 结点，然后后序遍历 F 结点的右子树

（20）F 结点的右子树为空，则返回

（21）逻辑返回到 F 结点，然后访问 F 结点，此时后序遍历 F 结点的左子树，后序遍历 F 结点的右子树，访问 F 结点的逻辑都已完成，则返回，F 结点出栈。

（22）逻辑返回到 C 结点，然后后序遍历 C 结点的右子树

（23）C 结点的右子树为空，则返回

（24）逻辑返回到 C 结点，然后访问 C 结点，此时后序遍历 C 结点的左子树，后序遍历 C 结点的右子树，访问 C 结点的逻辑都已完成，则返回，C 结点出栈。

（25）逻辑返回到 A 结点，然后访问 A 结点，此时后序遍历 A 结点的左子树，后序遍历 A 结点的右子树，访问 A 结点的逻辑都已完成，则返回，A 结点出栈。

（26）后序遍历二叉树已完成， 所以，后序遍历顺序为：DEBFCA

2、实现代码

#include <stdio.h>
#include <string.h>
#include <stdlib.h>

char *g_str = "ABD##E##CF###"; // 扩展二叉树前序序列
int g_index = 0;
typedef struct binary_node {
    char data;
    struct binary_node *lchild, *rchild;
}binary_tree;

void create_binary_tree(binary_tree **T) {
    if (strlen(g_str) == 0)
        return;
    
    if (g_str[g_index] == '#') {
        *T = NULL;
        g_index++;
    } else {
        *T = malloc(sizeof(**T));
        (*T)->data = g_str[g_index];
        g_index++;
        create_binary_tree(&(*T)->lchild);
        create_binary_tree(&(*T)->rchild);
    }
}

void visit_node(binary_tree *T) {
    printf("%c\n", T->data);
}

void pre_order_tree(binary_tree *T) {
    if (!T)
        return;
    
    visit_node(T);
    pre_order_tree(T->lchild);
    pre_order_tree(T->rchild);
}

void in_order_tree(binary_tree *T) {
    if (!T)
        return;
    
    in_order_tree(T->lchild);
    visit_node(T);
    in_order_tree(T->rchild);
}

void post_order_tree(binary_tree *T) {
    if (!T)
        return;
    
    post_order_tree(T->lchild);
    post_order_tree(T->rchild);
    visit_node(T);
}

/*销毁用后序遍历*/
void destroy_binary_tree(binary_tree *T) {
    if (!T)
        return;
    
    destroy_binary_tree(T->lchild);
    destroy_binary_tree(T->rchild);
    printf("%c\n", T->data);
    free(T);
}

int main(int argc, char *argv[]) {
    binary_tree *T;
    create_binary_tree(&T);
    printf("------后序遍历-------\n");
    post_order_tree(T);
    printf("------销毁二叉树------\n");
    destroy_binary_tree(T);
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1584834.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

RabbitMQ Docker 安装与应用

RabbitMQ Docker 安装与应用

1.官方镜像 该镜像包含用户操作界面 2.Docker运行&#xff0c;并设置开机自启动 docker run -d --restartalways --name rabbitmq -p 5672:5672 -p 15672:15672 rabbitmq:3.10-management 默认登录账户和密码 guest 3、使用 队列和交换机绑定
阅读更多...
Golang使用PGO优化程序性能

Golang使用PGO优化程序性能

文章目录 参考文章PGO是什么使用PGO的好处PGO做了什么热函数内联什么是内联内联的好处Go默认的内联策略查看内联预算PGO的热函数内联 去虚拟化调用指令高速缓存 PGO有什么缺点可执行程序变大构建时间变长 PGO怎么使用典型的工作流程收集CPU配置文件生产环境启动PGO代码改动重新…
阅读更多...
Linux进阶篇：磁盘管理（二）：LVM的创建、格式化和使用

Linux进阶篇：磁盘管理（二）：LVM的创建、格式化和使用

Linux磁盘管理&#xff08;二&#xff09;&#xff1a;LVM的创建、格式化和使用 一、LVM原理回顾 LVM的工作原理进行一个总结&#xff1a; (1)物理磁盘被格式化为PV&#xff0c;空间被划分为一个个的PE (2)不同的PV加入到同一个VG中&#xff0c;不同PV的PE全部进入到了VG的PE…
阅读更多...
【Android】apk安装报错：包含病毒: a.gray.BulimiaTGen.f

【Android】apk安装报错：包含病毒: a.gray.BulimiaTGen.f

​ 有时候apk安装或者更新时&#xff0c;显示&#xff1a;[高风险]包含病毒: a.gray.BulimiaTGen.f这种bug&#xff1b; 原因&#xff1a;这是手机管家误报病毒。 处理方法&#xff1a;我看网上其他资料可以进行申诉&#xff0c;也可以进行apk加固&#xff0c;我这边尝试用360…
阅读更多...
川土微高性能模拟芯片系列产品介绍和应用

川土微高性能模拟芯片系列产品介绍和应用

一、公司简介 上海川土微电子有限公司是一家成立于2016年的专注于高端模拟芯片研发设计与销售的高科技公司&#xff0c;产品涵盖隔离与接口、驱动与电源、高性能模拟三大产品线以及μMiC战略产品&#xff08; micro-Module in Chip&#xff09;。目前产品已广泛应用于工业控制…
阅读更多...
电脑干货：Win10系统中31个运维小技巧，值得收藏

电脑干货：Win10系统中31个运维小技巧，值得收藏

目录 技巧列表 今天给大家分享Win10系统中31个运维小技巧&#xff0c;希望对大家能有所帮助&#xff01; 技巧列表 1、查看电脑IP地址&#xff1a;按WinR打开运行框→输入cmd点确定→输入ipconfig回车就可以看到IP地址了。 2、网页上的文字不能复制怎么解决&#xff1a;按F12…
阅读更多...
【Linux】虚拟机连不上外网 (1)，2024百度网络安全岗面试真题收录解析

【Linux】虚拟机连不上外网 (1)，2024百度网络安全岗面试真题收录解析

vi /etc/sysconfig/network-scripts/ifcfg-ens33 BOOTPROTOstatic ONBOOTyes IPADDR? NETMASK? GATEWAY? dns18.8.8.8 dns1144.144.144.144 这两个必填 自我介绍一下&#xff0c;小编13年上海交大毕业&#xff0c;曾经在小公司待过&#xff0c;也去过华为、OPPO等大厂…
阅读更多...
SpringBoot学习之Kibana下载安装和启动（三十二）

SpringBoot学习之Kibana下载安装和启动（三十二）

一、简介 Kibana是一个开源的分析与可视化平台，设计出来用于和Elasticsearch一起使用的。你可以用kibana搜索、查看存放在Elasticsearch中的数据。Kibana与Elasticsearch的交互方式是各种不同的图表、表格、地图等，直观的展示数据，从而达到高级的数据分析与可视化的目的。 …
阅读更多...
vue3 + potree 渲染点云数据记录

vue3 + potree 渲染点云数据记录

potree 官网示例 前置条件&#xff1a; potree 无法直接加载 LAS&#xff0c;LCD&#xff0c;PLY等格式的点云文件, 需要通过 PotreeConverte 转换为 octree 数据格式&#xff0c;前端渲染中加载转换后的 json 格式 格式转换方向 .las ---- potreeConverter ----> .json…
阅读更多...
这4本计算机期刊，含CCF推荐，1个月发表周期，部分期刊剩15篇版面，接受预留

这4本计算机期刊，含CCF推荐，1个月发表周期，部分期刊剩15篇版面，接受预留

转眼间已进入四月份&#xff0c;正值春景好时节&#xff0c;在踏青赏景之余也别忘了做好科研&#xff08;学业&#xff09;规划。 我方致力于学术论文发表辅导十余年&#xff0c;与100余家国际出版社长期合作&#xff0c;推荐各领域论文至SCI/EI/CNKI收录期刊快速发表&#xf…
阅读更多...
Docker 安装 RocketMQ

Docker 安装 RocketMQ

目录 一、新建两个配置文件 1.1 创建docker-compose.yml文件 1.2 .新建broker.conf文件 二、运行 三、可视化界面 一、新建两个配置文件 1.1 创建docker-compose.yml文件 version: 3.5 services:rmqnamesrv:image: foxiswho/rocketmq:servercontainer_name: rmqnamesrvports…
阅读更多...
实战项目——智慧社区（一）

实战项目——智慧社区（一）

1、项目介绍 系统功能 登录、修改密码、登出 &#xff08;1&#xff09;首页 &#xff08;1.1&#xff09;数据统计&#xff1a;小区人员统计对比图&#xff0c;占比图 &#xff08;2&#xff09;物业管理 &#xff08;2.1&#xff09;小区管理&#xff1a;小区数据的增删改…
阅读更多...
【Cesium学习笔记】二、隐藏控件及按钮

【Cesium学习笔记】二、隐藏控件及按钮

【Cesium学习笔记】二、隐藏控件及按钮 一、隐藏控件二、隐藏cesium图标 Ps:本教程所有代码于同一个工程中&#xff0c;运行npm run dev默认首页为App.vue&#xff0c;只需替换App.vue的内容即可切换不同页面。 将上一节的App.vue保存为类似“加载cesium.vue”这种对应名称。 …
阅读更多...
回归预测 | Matlab实现WOA-GPR鲸鱼算法优化高斯过程回归多变量回归预测

回归预测 | Matlab实现WOA-GPR鲸鱼算法优化高斯过程回归多变量回归预测

回归预测 | Matlab实现WOA-GPR鲸鱼算法优化高斯过程回归多变量回归预测 目录 回归预测 | Matlab实现WOA-GPR鲸鱼算法优化高斯过程回归多变量回归预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 Matlab实现WOA-GPR鲸鱼算法优化高斯过程回归多变量回归预测 1.Matlab实现…
阅读更多...
解决Android Studio Loading Devices问题

解决Android Studio Loading Devices问题

目录 一、解决办法&#xff08;普通&#xff09;&#xff1a; 二、解决办法的优化 三、解决办法的进一步优化 问题&#xff1a;windows 11 电脑&#xff0c;每次开机&#xff0c;打开Android Studio,都会显示Loading Devices&#xff0c;连接不上设备。 原因&#xff1a;adb…
阅读更多...
SpringBoot和Vue2项目配置https协议

SpringBoot和Vue2项目配置https协议

1、SpringBoot项目 ① 去你自己的云申请并下载好相关文件&#xff0c;SpringBoot下载的是Tomcat&#xff08;默认&#xff09;&#xff0c;Vue2下载的是Nginx ② 将下载的压缩包里面的.pfx后缀文件拷贝到项目的resources目录下 ③ 编辑配置文件 &#xff08;主要是框里面的内…
阅读更多...
SOCKS代理是如何提高网络性能和兼容性的？

SOCKS代理是如何提高网络性能和兼容性的？

SOCKS代理作为一种网络协议中间件&#xff0c;不仅在提升网络隐私和安全性方面发挥着重要作用&#xff0c;也在提高网络性能和兼容性方面有着不容忽视的影响&#x1f680;。本文将深入探讨SOCKS代理如何通过减少网络延迟&#x1f680;、优化数据传输&#x1f504;、提高跨平台兼…
阅读更多...
MacOS下Qt 5开发环境安装与配置

MacOS下Qt 5开发环境安装与配置

最近笔者在MacOS中使用Qt Creator开发Qt程序时遇到了一些问题&#xff0c;在网上查了不少资料&#xff0c;都没有找到解决方案&#xff0c;只有自己进行研究摸索了&#xff0c;今天晚上终于将目前遇到的问题全部解决了&#xff0c;特记录下来分享给大家。 笔者使用的是MacOS 1…
阅读更多...
政安晨：【深度学习神经网络基础】（六）—— 前馈神经网络

政安晨：【深度学习神经网络基础】（六）—— 前馈神经网络

目录 简述 前馈神经网络结构 计算输出 初始化权重 径向基函数神经网络 径向基函数 政安晨的个人主页&#xff1a;政安晨 欢迎 &#x1f44d;点赞✍评论⭐收藏 收录专栏: 政安晨的机器学习笔记 希望政安晨的博客能够对您有所裨益&#xff0c;如有不足之处&#xff0c;欢迎…
阅读更多...
“反正你又看不到，少写一行又何妨......”

“反正你又看不到，少写一行又何妨......”

单链表专题 1.链表的概念及结构2. 实现单链表3. 链表的分类 1.链表的概念及结构 概念&#xff1a;链表是⼀种物理存储结构上⾮连续、⾮顺序的存储结构&#xff0c;数据元素的逻辑顺序是通过链表中的指针链接次序实现的 。 链表的结构跟火车车厢相似&#xff0c;淡季时⻋次的⻋厢…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023