文章目录
- 每日碎碎念
- 一、题目要求及测试点
- 35 搜索插入位置
- 测试点
- 提示
- 二、题解
- 自己上手
- 正经题解
- 暴力法
- 二分法之优化了一下逻辑
- 三、总结
每日碎碎念
苦痛生活继续
hello LeetCode,今天还是数组二分专项刷题…
一、题目要求及测试点
35 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
链接https://leetcode.cn/problems/search-insert-position/description/
测试点
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
提示
- 1 < = n u m s . l e n g t h < = 1 0 4 1 <= nums.length <= 10^4 1<=nums.length<=104
- − 1 0 4 < = n u m s [ i ] < = 1 0 4 -10^4 <= nums[i] <= 10^4 −104<=nums[i]<=104
- nums 为 无重复元素 的升序 排列数组
- − 1 0 4 < = t a r g e t < = 1 0 4 -10^4 <= target <= 10^4 −104<=target<=104
二、题解
自己上手
代码如下:
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1;
int middle = left + ((right - left) / 2);
while (left <= right){
middle = left + ((right - left) >> 1);
if (target < nums[middle])
right = middle - 1;
else if (target > nums[middle])
left = middle + 1;
else
return middle;
}
if (target > nums[middle])
return (middle + 1);
else
return middle;
}
};
来点无用总结:
时间复杂度O(logn),如果找到就是二分,重点是没找到的插入,肯定是循环退出right<left的情况啦,如果target>nums[middle],这时显然后插middle+1,不然就插在当前middle位置…
正经题解
提示中已说明该数列有序,且无重复,考虑二分; 当然,暴力解法不一定时间消耗就很高…
数组中插入目标值有四种情况:
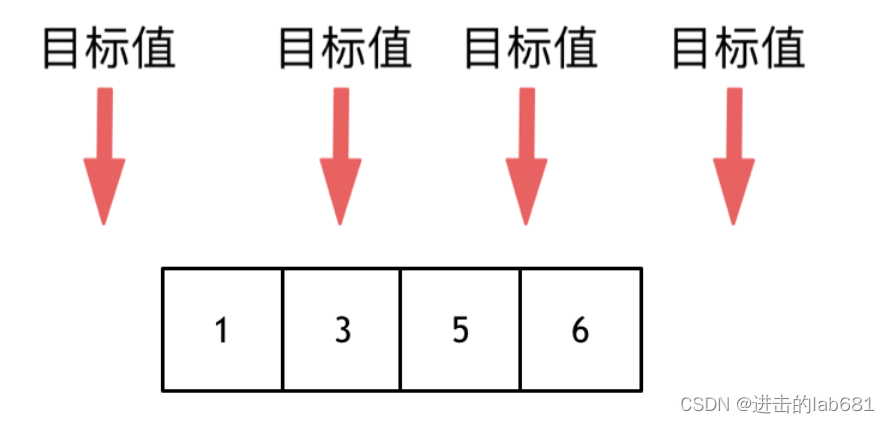
- 目标值在数组所有元素之前
- 目标值等于数组中某一个元素
- 目标值插入数组中的位置
- 目标值在数组所有元素之后
暴力法
暴力的逻辑简单,因为原数列就有序,就从左到右遍历,一旦发现target<=数组中某个数,就返回该数下标即可;如果遍历完,考虑万一插在数列最后的情况,即返回数列长度即可
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
for (int i=0; i < nums.size(); i++){
if (target <= nums[i])
return i;
}
return nums.size();
}
};
时间复杂度:O(n),空间复杂度:O(1)
二分法之优化了一下逻辑
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1;
while (left <= right){
int middle = left + ((right - left) >> 1);
if (target < nums[middle])
right = middle - 1;
else if (target > nums[middle])
left = middle + 1;
else
return middle;
}
return left; //right+1
}
};
当最后middle=left=right即将退出时
target<nums[middle],left=middle,right=middle-1,要插middle位置,即返回left或者right+1;
target>nums[middle],right=middle,left=middle+1,要插middle+1位置,即返回left或者right+1;
两种情况合并即可
时间复杂度:O(log n),空间复杂度:O(1)
三、总结
1.注意二分法使用前提;
2.理清楚边界条件
3.nums.size(),编程规范注意一下