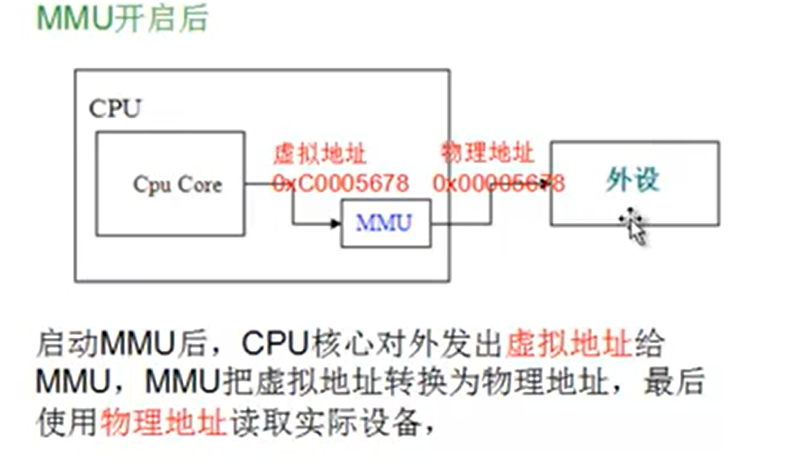
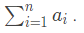回溯算法的应用

news2025/8/4 1:29:37

基本思想：

回溯法从开始结点(根结点)出发,以深度优先方式搜索整个解空间。这个开始结点成为活结点,同时也成为当前的扩展结点。在当前扩展结点处,搜索向纵深方向移至一个新结点。这个新结点成为新的活结点,开成为当前扩展结点。如果在当前扩展结点处不能再向纵深方向移动,则当前扩展结点就成为死结点。此时,应往回移动(回溯)至最近的活结点处,并使这个活结点成为当前扩展结点。回溯法以这种工作方式递归地在解空间中搜索,直至找到所要求的解或解空间中已无活结点时为止。

例：对于n=3时的0-1背包问题,考虑下面的具体实例:w=[16,15,15],p=[45，25,25],c=30。

解空间：(三种物品的所有可能)

每一层的根节点对应某种物品。第一层是第一件物品，第二层时第二件物品，第三层是第三件物品。左子树表示装入下一件物品，右子树表示不装下一件物品

开始时,根结点是唯一的活结点,也是当前扩展结点。在这个扩展结点处,可以沿纵深方向移至结点B或结点C。
假设选择先移至结点B。此时,结点A和结点B是活结点,结点B成为当前扩展结点。由于选取了w1,故在结点B处剩余背包容量是r=14,获取的价值为45。
从结点B处,可以移至结点D或E。由于移至结点D至少需要w2=15的背包容量,而现在仅有的背包容量是r=14,故移至结点D导致不可行解。搜索至结点E不需要背包容量,因而是可行的。从而选择移至结点E。此时,E成为新的扩展结点,结点A,B和E是活结点。在结点E处,r=14,获取的价值为45。
从结点E处,可以向纵深移至结点J或K。移至结点J导致不可行解,而移向结点K是可行的,于是移向结点K,它成为新的扩展结点。由于结点K是叶结点,故得到一个可行解。这个解相应的价值为45。Xi的取值由根结点到叶结点K的路径唯一确定,即x=(1,0,0)。
由于在结点K处已不能再向纵深扩展,所以结点K成为死结点。返回到结点E处。此时在结点E处也没有可扩展的结点,它也成为死结点。接下来又返回到结点B处。结点B同样也成为死结点,从而结点A再次成为当前扩展结点。
结点A还可继续扩展,从而到达结点C。此时,r=30,获取的价值为0。
从结点C可移向结点F或G。假设移至结点F,它成为新的扩展结点。结点A,C和F是活结点。在结点F处,r=15,获取的价值为25。从结点F,向纵深移至结点L处,此时,r=0,获取的价值为50。由于L是叶结点,而且是迄今为止找到的获取价值最高的可行解,因此记录这个可行解。
结点L不可扩展,又返回到结点F处。按此方式继续搜索,可搜索遍整个解空间。搜索结束后找到的最好解是相应0-1背包问题的最优解。

回溯算法的装载问题

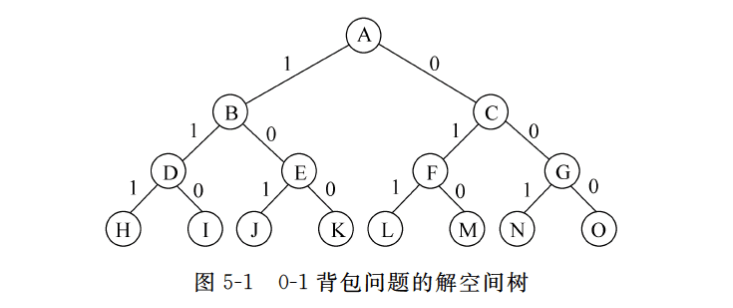
有一批共n个集装箱要装上两艘载重量分别为 $C_{1}$ 和 $C_{2}$ 的轮船,其中,集装箱 i 的重量为 $W_{i}$ ，

$\sum_{i=1}^{n}w_{i}=c_{1}+c_{2}$
装载问题要求确定是否有一个合理的装载方案可将这n个集装箱装上这两艘轮船。如果有,找出一种装载方案。

基本思路：

(1）首先将第一艘轮船尽可能装满。

(2）将剩余的集装箱装上第二艘轮船。
将第一艘轮船尽可能装满等价于选取全体集装箱的一个子集,使该子集中集装箱重量之和最接近c1。由此可知,装载问题等价于以下特殊的0-1背包问题。
将每个物品的装与不装化成解空间

回溯算法思想

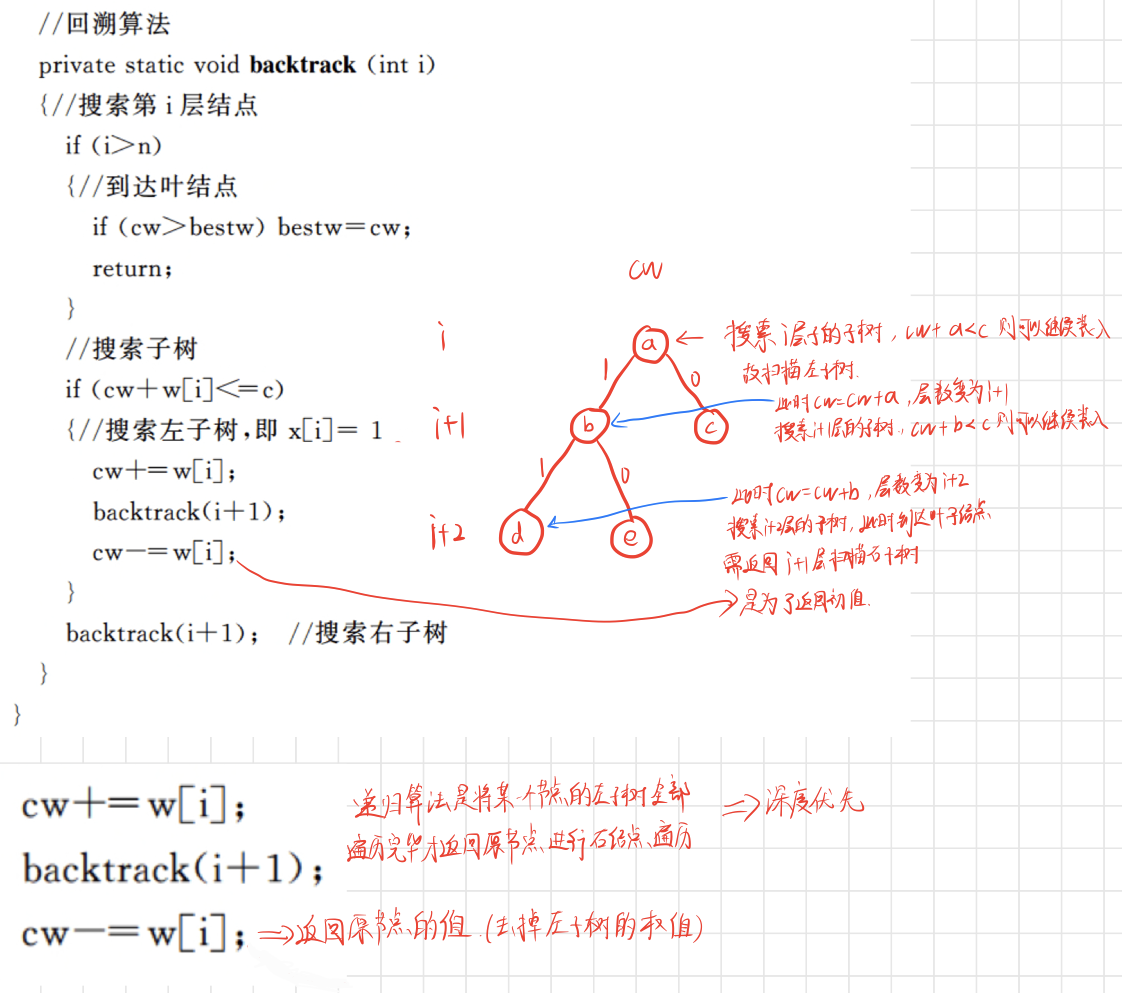
算法maxLoading调用递归方法 backtrack(1)实现回溯搜索。backtrack(i)搜索子集树中第i层子树。

类Loading 的数据成员记录子集树中结点信息

cw记录当前结点相应的装载重量

bestw记录当前最大装载重量。

在算法backtrack 中

当i≥n时,算法搜索至叶结点,其相应的装载重量为cw。如果cw>bestw ,则表示当前解优于当前最优解,此时应更新bestw。
当i≤n时,当前扩展结点Z是子集树的内部结点。该结点有:x[i]=1和x[i]=0两个儿子结点。

其左儿子结点表示x[i]=1的情形,仅当cw＋w[i]≤c时进入左子树,对左子树递归搜索。

其右儿子结点表示x[i门=0的情形。由于可行结点的右儿子结点总是可行的,故进入右子树时不需检查可行性。

public class Loading {
    //类数据成员
    static int n;   //集装箱数
    static int[] w;//集装箱重量数组
    static int c;//第一艘轮船的载重量
    static int cw;//当前载重量
    static int bestw;//当前最优载重量
    private static int maxLoading(int[]ww,int cc){
        //初始化数据成员
        n=ww.length-1;
        w=ww;
        c=cc;
        cw=0;
        bestw=0;
        
        //计算最优载重量
        backtrack(1);
        return bestw;
    }

    private static void backtrack(int i) {
        //搜索第i层结点
        if (i>n){//到达叶子节点
            if (cw>bestw) bestw =cw;  //更新最优载重
            return;
        }else{//未到达叶子节点
            if (cw+w[i]<=c){  //表示装上i层的节点后还能继续装
                cw+=w[i];//更新当前载重
                backtrack(i+1);//搜索下一层，直至搜索玩所有左子树，再遍历右子树
                cw-=w[i];//恢复遍历某个左节点之前的最初状态，便于遍历右子树
            }
            backtrack(i+1);//遍历右子树，无需装入，直接下一层
        }
    }

}

上界函数

cw+r ≤ bestw表示货物总质量可以全部装进去，所以只需要左子树即可。

在算法中记录与当前最优值相应的当前最优解。在类Loading中增加两个私有数据成员α和 bestx,x用于记录从根至当前结点的路径, bestx记录当前最优解。算法搜索到达叶结点处,就修正bestx的值。

public class Loading2 {
    static int n;   //集装箱数
    static int[] w;//集装箱重量数组
    static int c;//第一艘轮船的载重量
    static int cw;//当前载重量（重量）
    static int bestw;//当前最优载重量（重量）
    static int r;//剩余集装箱重量、
    static int[] bestx;//记录当前最优解（路径）
    static int[]x;//当前解（路径）
    public static int maxLoading(int []w, int c, int[] bestx){
        //迭代回溯法
        //返回最优载重及其相应的解
        //初始化根节点
        int i =1;
        int n=w.length-1;
        int []x = new int[n+1];
        bestw =0;
        r=0;
        for(int j=0; j<=n; j++){
            r=r+w[j];
        }
        //搜索子树（进入子树）
        while (true){
            while (i<=n&&cw+w[i]<=c){//进入节点i的左子树，层数变为i+1
                r-=w[i];//剩余货物减少，节点i装入
                cw+=w[i];//当前载货量
                x[i]=1;//左子树，装入
                i++;//层数变化
            }
            if (i>n){
                //到达叶节点
                for (int j=1;j<=n;j++){
                    bestx[j]=x[j];//每次到叶节点更新最佳路径解
                }
                bestw = cw;//更新最优装载值
            }else {
                //进入右子树
                r-=w[i];//剩余货物减少，节点i装入，层数变为i+1
                x[i]=0;
                i++;
            }
            //从叶子节点返回根节点
            while (cw+r<=bestw){
                //剪枝回溯
                i--;//回溯
                while (i>0&&x[i]==0){//未到根节点且为右子树
                    r+=w[i];//从右子树返回
                    i--;
                }
                if (i==0) return bestw;//回到根节点
                //进入右子树
                x[i]=0;
                cw-=w[i];
                i++;
            }

        }
    }
}