LeetCode[662]二叉树的最大宽度

news2025/8/6 1:59:22

难度：中等

题目：

给你一棵二叉树的根节点 root ，返回树的 最大宽度 。

描述：

树的 最大宽度 是所有层中最大的宽度。

每一层的宽度被定义为该层最左和最右的非空节点（即，两个端点）之间的长度。将这个二叉树视作与满二叉树结构相同，两端点间会出现一些延伸到这一层的 null 节点，这些 null 节点也计入长度。

题目数据保证答案将会在 32 位 带符号整数范围内。

示例 1：

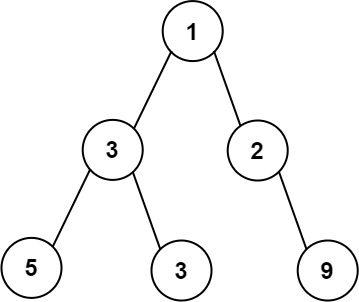
输入：root = [1,3,2,5,3,null,9]
输出：4
解释：最大宽度出现在树的第 3 层，宽度为 4 (5,3,null,9) 。

示例 2：

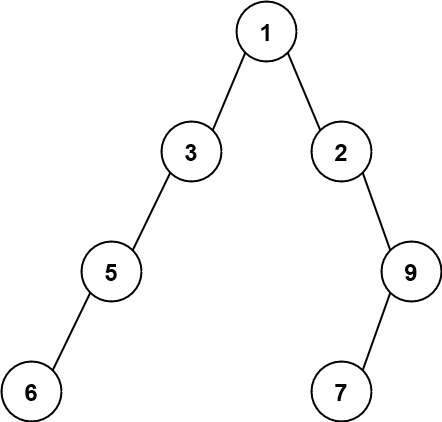
输入：root = [1,3,2,5,null,null,9,6,null,7]
输出：7
解释：最大宽度出现在树的第 4 层，宽度为 7 (6,null,null,null,null,null,7) 。

示例 3：

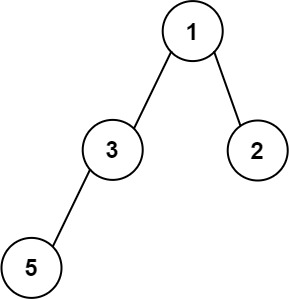
输入：root = [1,3,2,5]
输出：2
解释：最大宽度出现在树的第 2 层，宽度为 2 (3,2) 。

提示：

树中节点的数目范围是 [1, 3000]
-100 <= Node.val <= 100

重点！！！解题思路

第一步：

此题我们应该判断每一层的宽度然后做比较

所以我们采用队列的思想来存储每一层

遍历完一层，我们就给这一层poll出去，遍历下一层

并且每次更新宽度

第二步：

可以把树的左右子节点设置编号方便计算宽度

根节点编号为0（当作n看），它的左子树编号为2*n，它的右子树编号为2*n+1

需要每次循环时更新子树的编号

明白上述思想请看下面讲解

源码+讲解：

class Solution {
    class PNI{  //定义一个结构体，每个节点对应一个编号
        TreeNode root;
        int n;

        public PNI(TreeNode root, int n) {
            this.root = root;
            this.n = n;
        }
    }
    public int widthOfBinaryTree(TreeNode root) {
       Queue<PNI> queue = new ArrayDeque<>();  //队列来存储结构体
       queue.offer(new PNI(root,0));  //先添加根节点
       int ans=0;  //返回的值  每次循环跟新此值
       while (!queue.isEmpty()){  //遍历树的每层节点
           int size=queue.size();  
           int l=queue.peek().n;  //树最左面的节点编号
           int r=0;  //树每一层的编号更新
           for (int i = 0; i < size; i++) {
               PNI temp = queue.poll();
               r= temp.n-l;  //每个节点在每一层的编号
               if (temp.root.left!=null){
                   queue.offer(new PNI(temp.root.left,r*2));
               }
               if (temp.root.right!=null){
                   queue.offer(new PNI(temp.root.right,r*2+1));
               }
           }
           ans=ans>r+1?ans:r+1;  //r+1为当前层宽度
       }
       return ans;
    }

}

运行结果：