例题一

解法:
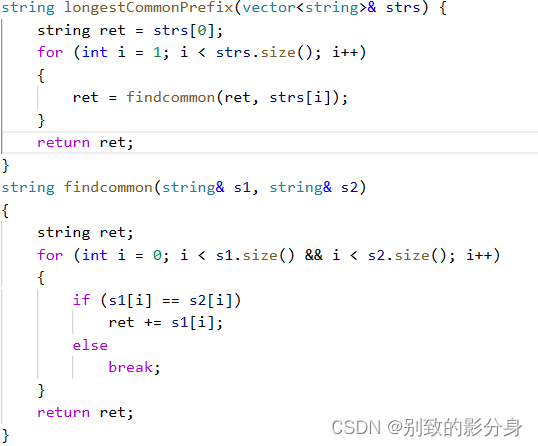
算法思路(两两⽐较):
我们可以先找出前两个的最⻓公共前缀,然后拿这个最⻓公共前缀依次与后⾯的字符串⽐较,这样就可以找出所有字符串的最⻓公共前缀。
例题二

解法(中⼼扩散):
算法思路:
枚举每⼀个可能的⼦串⾮常费时,有没有⽐较简单⼀点的⽅法呢?
对于⼀个⼦串⽽⾔,如果它是回⽂串,并且⻓度⼤于 2,那么将它⾸尾的两个字⺟去除之后,它仍然是个回⽂串。如此这样去除,⼀直除到⻓度⼩于等于 2 时呢?⻓度为 1 的,⾃⾝与⾃⾝就构成回⽂;⽽⻓度为 2 的,就要判断这两个字符是否相等了。从这个性质可以反推出来,从回⽂串的中⼼开始,往左读和往右读也是⼀样的。那么,是否可以枚举回⽂串的中⼼呢?
从中⼼向两边扩展,如果两边的字⺟相同,我们就可以继续扩展;如果不同,我们就停⽌扩展。这样只需要⼀层 for 循环,我们就可以完成先前两层 for 循环的⼯作量。

例题三

解法(模拟⼗进制的⼤数相加的过程):
算法思路:
模拟⼗进制中我们列竖式计算两个数之和的过程。但是这⾥是⼆进制的求和,我们不是逢⼗进⼀,⽽是逢⼆进⼀。

例题四

解法(⽆进位相乘然后相加,最后处理进位):
算法思路:
整体思路就是模拟我们⼩学列竖式计算两个数相乘的过程。但是为了我们书写代码的⽅便性,我们选择⼀种优化版本的,就是在计算两数相乘的时候,先不考虑进位,等到所有结果计算完毕之后,再去考虑进位。如下图: