对比学习踩坑记录

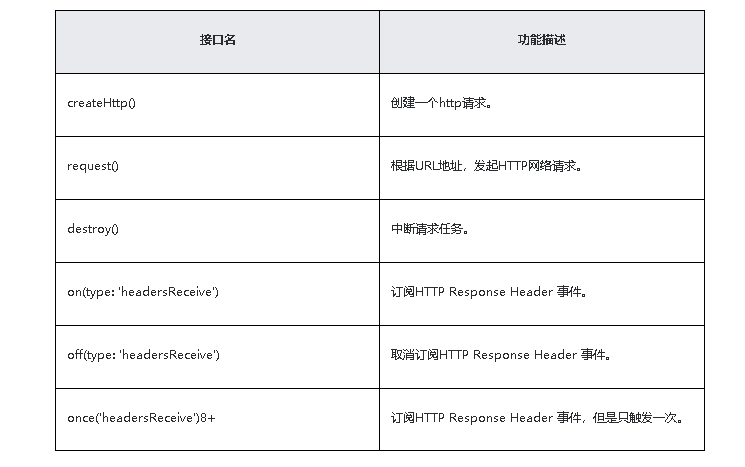
本文是对过去几个月来利用对比学习的思想来优化多模态学习任务的思路的总结，主要包含以下几个方面：为什么要用对比学习、跨模态中对比学习怎么用、对比的过程中负样本是不是越多越好、要不要推远所有的负样本、样本之间的语义碰撞如何缓解、什么是负样本的“逃票”现象以及最重要的问题：如何学到一个高效的表征空间？

为什么要用对比学习

对比学习的核心在于通过比较和区分不同样本间的相似性和差异性，推动模型学习更为精准和普适的特征表示。随着多模态场景下对比学习的广泛使用，特别是CLIP利用其进行的大规模无监督学习，展现出扩模态对比学习的几大关键优势：
1.学习语义关联：对比学习的目标是最大化同一对图文样本的相似度，同时最小化不同图文对之间的相似度。这种方法鼓励模型学习图像和文本之间深层次的语义联系，而不是浅层特征。
2.泛化能力增强：通过对比学习，CLIP能够习得更加通用的图 像和文本表示，使其在零样本（zero-shot）设置下也能较好地迁移至新的分类或检索任务，无需针对特定任务重新训练。
3.更好利用负样本：对比学习框架下的负样本是指与正样本不匹配的图文对。在CLIP中，合理处理负样本能促使模型不仅关注正确匹配，而且学会鉴别哪些是不匹配的组合，从而提高模型区分能力和表达能力。
综上所述，对比学习在扩模态对齐任务中应用的核心问题，是它解决了如何在无标注的大规模数据上建立图像和文本之间的语义对应关系，理解并挖掘它们内在的一致性，从而实现对复杂数据的深度解读和有效利用。

对比学习应该怎么用

我们可以借用上图所示的猫狗大战例子来将对比学习的主题思想具象化。对比学习无非就一个目标，在表征空间上拉近正类样本的同时，推远负类样本。假设$x_1$是基准点anchor，我们的学习目标也就是让$x_1$和$x_2$更近，并推远$x_3$
将上述过程用公式来表示：
$$s(f(x),f(x_{+}))>>s(f(x),f(x_{-}))$$
最终目标是使正样本与锚点的相似度远远大于负样本与锚点的相似度，即缩小与正样本间的距离，扩大与负样本间的距离，使正样本与锚点的距离远远小于负样本与锚点的距离，从而得到表征良好的特征空间

下面主要从CLIP的算法角度来看看主流的对比学习方法是怎么优化表征空间的
$$\begin{array}{c}{\mathcal{L}}_{\text{i2t}}=-\sum _{i=1}^N\log \frac{\exp (\text{sim}(I_i,T_i)/\tau )}{{\sum }_{j=1}^N\exp (\text{sim}(I_i,T_j)/\tau )}\end{array}$$
以img2txt的对比过程为例(也就是从矩阵的每一行来看)， CLIP uses matched image-text pairs as positive samples, while unmatched ones as negative samples. 其实上述公式还可以继续简化，如下所示：
$$\begin{array}{c}{\mathcal{L}}_{\text{i2t}}=-\log \frac{S_p}{S_p+S_n}\end{array}$$
网络的优化目标很简单，最大化matched pairs similarity $S_p$，直到${\mathcal{L}}_{\text{i2t}}$收敛为止.

“推远所有”还是“有所保留”

从MOCO中我们得到一个经验，对比的过程中负样本是越多越好的（这一点其实在CLIP的大规模预训练中也有体现），所以MOCO引入了negative samples queue来尽可能多地暂存负样本，让网络区分正负样本间的差异性。但其实这种先验也不绝对，或者说它更适用于类间差异性大的数据集，如猫狗之间的对比，这里不展开，下一段会详细解释。
对于跨模态学习的任务，我们也可以借鉴negative samples queue的设计，让负样本尽可能多。但是在引入queue后我们发现，负样本增加的同时也会出现很多与正样本相近的样本，例如，“someone drinks a cup of tea” and "she talks on the phone while drinking tea"对齐的是不同的图像，但是其语义上有非常大的重叠，而由于对比学习选择的是成对且唯一的正样本对，所以优化过程才不会管你语义空间是否相近，统统推远，所以这点是有问题的。
所以很直观的一种做法是：从单一模态中预先挑选相似度小于指定阈值的样本来对比。例如，在上述例子中，“someone drinks a cup of tea” and "she talks on the phone while drinking tea"这两句话的语义其实是很相关的，相应的语义相似度的值也就高，但是"someone drinks a cup of tea"与"pizza on the table"没有什么关联，语义相似度的值也低，拿这种相似度得分低的样本来对比是比较合适的。所以总结一下，在这一步中，我们发现经过编码器后，在语义空间上相近的样本没有必要全部推远，所以我们通过设定阈值挑选与当前样本同模态的低相似度负样本进行对比，将其推远，对比学习的公式其实没变化。

负样本是不是越多越好？样本之间的语义碰撞如何缓解?

对比学习的一个常见假设是，大量负样本有助于学习更好的表示，因为在每个训练批次中，模型能够对比更多的语义表征，从而学会区分。然而，《A Theoretical Analysis of Contrastive Unsupervised Representation Learning》表明这一假设并不总是成立的，并且当存在大量负样本时，观察到具有高语义重叠的负样本的机会增加。
例如，对于"someone drinks a cup of tea"而言，“cut tomato and put it in a bowl” and "cut tomatoes and mix with the herbs"可能都是低于预设相似度阈值的负样本，但是可以看出，这两个负样本之间是存在语义重叠的(semantic overlap)。如果网络在对比的过程中过于关注这些语义重叠样本，很大程度上会丢弃学习到的普适性、通用性特征，这种现象被称作“语义碰撞”(semantic collision)。也就是说，如果对比过程中存在大量的语义碰撞问题，那么会阻止网络学到好的表征。
因此，需要对挑选出的负样本中去除flase negatives，但是有没有直接的信息能够证明哪个样本是False negative，所以这里引入负样本集修剪策略。简单来说，就是对挑选出的负样本集进行互相似度计算，得到每个样本与其他样本的相似度均值C，这里称之为连通性，其计算方式如下：
$$\begin{array}{c}C(x_i)=\frac{1}{M}\sum _{j=1}^M\frac{x_i^T{x}_j}{||x_i||\cdot ||x_j||}\end{array}$$
显然，连通性越高的样本在负样本集中的重叠程度也就越高，所以我们可以跟上一节一样，用预设的连通性阈值对负样本集进行挑选，滤除高重叠样本得到语义稀疏的样本，优化对比过程中的表征空间分布。本小结的具体做法感兴趣的朋友，可以阅读2021年的CrossCLR。

什么是负样本逃票现象

在上述的负样本集筛选过程中，会出现一个比较极端的现象，这里仅提出供大家参考，相应的解决方法暂时还没有找到。。。
首先我们回顾一下负样本挑选过程中使用的两点策略。首先是使用与图像匹配的positive text，计算其与negative text的相似度，拿预设的阈值去挑选与positive text在原始语义空间接近的样本点（“someone drinks a cup of tea” and “she talks on the phone while drinking tea”），不去动这些样本点，而是推远低于这个阈值的负样本点，注意这里是用positive text去挑选的。而后，为了缓解语义碰撞，我们拿上一步挑出来的negative samples，计算两两之间的相似度均值，利用阈值再挑选出语义稀疏的样本点，避免丢失了学到的普适性特征，注意这里用的都是挑选出来的negative samples。
在上述的对比过程中，负样本肯定是越选越少，虽然最后计算的是每个样本的均值，但是在每个iteration优化的过程中，模型会学到偷懒的策略：既然我们的优化目标是让损失趋向于零，也就是让$\frac{S_p}{S_p+S_n}$趋向于1，最简单的方法就是在挑选的过程中把所有$S_n$都挑出去，也就是负样本集为空了，损失自然是$-\log (1)=0$。我在实验过程中发现了上述负样本“逃票”问题，但是暂时还没找到缓解的办法。。
$$\begin{array}{c}{\mathcal{L}}_{\text{i2t}}=-\log \frac{S_p}{S_p+S_n}\end{array}$$

如何学到一个高效的表征空间

感觉自己现在还没有能力回答好这个问题，留个坑以后来填！