首先是图的表示,邻接矩阵和邻接表。实现看代码
- 邻接矩阵:二维数组,
- matrix[a][b] 表示 从a可以指向b
- 无向图而言, matrix[a][b]=matrix[b][a],比如可以定义matrix[a][b]=1表示ab是连接的,matrix[a][b]=0表示ab是不可连接的
- 有向图:matrix[a][b]=x,表示从a到b的权是x,如果matrix[a][b]=无穷大,表示ab是不可连接的
- 邻接表:
- 外层是一个数组,数组长度表示图中有多少个节点,数组下标对应节点a
- 每个数组中,存放一个链表,链表的每个节点也是数组
- 链表长度代表从a可以直接指向多少个节点
- 链表元素树一个数组,数组第一个元素代表被执向的b,第二个元素代表a到b的权
个人感觉,邻接矩阵适合无向图,邻接表适合有向图。
/**
* 邻接矩阵
*
* @param n 初始化图中节点的个数
* @param edges edges边,从edge[0]指向edge[1],路径长度为edge[2]
* @return matrix
*/
public int[][] adjacentMatrix(int n, int[][] edges) {
// 邻接矩阵就是一个二维数组,很好理解,对应坐标的值是路径长度
int[][] matrix = new int[n][n];
for (int[] edge : edges) {
int start = edge[0];
int end = edge[1];
int length = edge[2];
matrix[start][end] = length;
}
return matrix;
}
public List<int[]>[] adjacentList(int n, int[][] edges) {
// 邻接列表,最外层是个数组,数组元素是一个列表
// 列表中存储的数据,又是一个数组
// 最外层数组,坐标代表edge[0]
// 数组元素是个列表,这个列表存储的东西是 edge[1],edge[2]
// 每个链表有多少元素,就说明这个点指向多少个别的点
List<int[]>[] list = new List[n];
for (int i = 0; i < n; i++) {
list[i] = new ArrayList<>();
}
for (int[] edge : edges) {
int start = edge[0];
int end = edge[1];
int length = edge[2];
list[start].add(new int[] {end, length});
}
return list;
}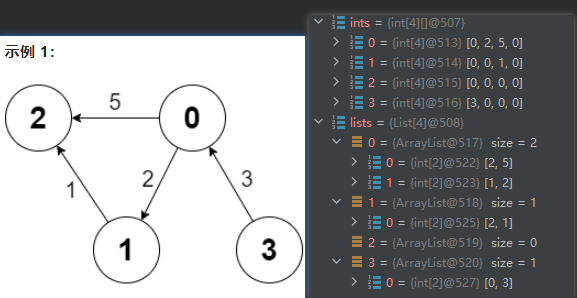
2642. 设计可以求最短路径的图类
比如我们求从0 到其他点的最短距离,定义一个数组,第0行分别是每个节点,第一行是0到其他节点的距离,初始化为正无穷大,第三行是表示是否已经是最小距离。
| 0 | 1 | 2 | 3 |
| 0 | ∞ | ∞ | ∞ |
| T | F | F | F |
首先遍历0能够直接到达的顶点,修改如下,此时0到1的距离是最短的,可以标记为T
| 0 | 1 | 2 | 3 |
| 0 | 2 | 5 | ∞ |
| T | T | F | F |
然后看从2出发,能够直接到达的距离
因为从1到2的距离是2+1,小于当前的5,因此可以刷新下表,此时得到了0到2最短距离3
| 0 | 1 | 2 | 3 |
| 0 | 2 | 3 | ∞ |
| T | T | T | F |
思路就是上面的思路,不断的获取距离,然后和当前的距离比较,如果比他小,就更新进去。
public class Graph {
List<int[]>[] graph;
public Graph(int n, int[][] edges) {
graph = adjacentList(n, edges);
}
public List<int[]>[] adjacentList(int n, int[][] edges) {
List<int[]>[] list = new List[n];
for (int i = 0; i < n; i++) {
list[i] = new ArrayList<>();
}
for (int[] edge : edges) {
int start = edge[0];
int end = edge[1];
int length = edge[2];
list[start].add(new int[] {end, length});
}
return list;
}
// 向边集中添加一条边,本题的数据保证添加这条边之前对应的两个节点之间没有有向边
// 这说明添加不会产生新的节点。即邻接矩阵外层的数组长度不会改变,只会改变数组元素的链表
public void addEdge(int[] edge) {
int start = edge[0];
int end = edge[1];
int length = edge[2];
graph[start].add(new int[] {end, length});
}
public int shortestPath(int node1, int node2) {
// 如果是同一个端点,说明路径为0,直接返回即可
if (node1 == node2) {
return 0;
}
// 定义一个距离数组,用于标识从当前node1出发,到所有点的最短路径,初始化值为Integer.MAX_VALUE,表示无穷大
int[] distance = new int[graph.length];
Arrays.fill(distance, Integer.MAX_VALUE);
// node1到自身的距离为0;
distance[node1] = 0;
// 参考BFS,定义一个队列
Queue<int[]> queue = new LinkedList<>();
// 把node1变成节点传入队列中,队列存一个长度2的数组,分别表示到这个节点,距离
queue.offer(new int[] {node1, 0});
while (!queue.isEmpty()) {
int[] poll = queue.poll();
int cur = poll[0];
int cost = poll[1];
// if (cur == node2) {
// return cost;
// }
// 从邻接列表中取出当前节点可以指向的节点list,遍历这个list
List<int[]> list = graph[cur];
for (int[] arr : list) {
int next = arr[0];
int ncost = arr[1];
// 如果路径和比当前小,就更新进去
if (distance[next] > cost + ncost) {
distance[next] = cost + ncost;
queue.offer(new int[] {next, cost + ncost});
}
}
}
return distance[node2] == Integer.MAX_VALUE ? -1 : distance[node2];
}
}
// 优化,如果我们定义一个优先级队列,这样每次BFS的时候,都会先遍历路径最小的节点
// 这样的话,就可以在while循环里面进行判断,如果等于目标节点,就可以直接返回了
Queue<int[]> queue = new PriorityQueue<>((a, b) -> a[1] - b[1]);