每日一练：LeeCode-200、岛屿数量【DFS递归+BFS队列】

news2024/11/15 9:24:43

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

输入：grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
输出：1

示例 2：

输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 '0' 或 '1'

方法1：DFS(系统栈=递归)

这题让求的是岛屿的数量，二维数组中值是1的都是岛屿，如果多个1是连着的，那么他们只能算一个岛屿。

思路：

最简单的一种方式就是遍历数组中的每一个值，如果是1就说明是岛屿，然后把它置为0或者其他的字符都可以，只要不是1就行，然后再遍历他的上下左右4个位置。如果是1，说明这两个岛屿是连着的，只能算是一个岛屿，我们还要把它置为0，然后再以它为中心遍历他的上下左右4个位置……。如果是0，就说明不是岛屿，就不在往他的上下左右4个位置遍历了。这里就以示例1为例来看一下

在这里插入图片描述

public int numIslands(char[][] grid) {
    //边界条件判断
    if (grid == null || grid.length == 0)
        return 0;
    //统计岛屿的个数
    int count = 0;
    //两个for循环遍历每一个格子
    for (int i = 0; i < grid.length; i++)
        for (int j = 0; j < grid[0].length; j++) {
            //只有当前格子是1才开始计算
            if (grid[i][j] == '1') {
                //如果当前格子是1，岛屿的数量加1
                count++;
                //然后通过dfs把当前格子的上下左右4
                //个位置为1的都要置为0，因为他们是连着
                //一起的算一个岛屿，
                dfs(grid, i, j);
            }
        }
    //最后返回岛屿的数量
    return count;
}

//这个方法会把当前格子以及他邻近的为1的格子都会置为0
public void dfs(char[][] grid, int i, int j) {
    //边界条件判断，不能越界
    if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] == '0')
        return;
    //把当前格子置为0，然后再从他的上下左右4个方向继续遍历
    grid[i][j] = '0';
    dfs(grid, i - 1, j);//上
    dfs(grid, i + 1, j);//下
    dfs(grid, i, j + 1);//左
    dfs(grid, i, j - 1);//右
}

方法2：BFS(队列)

DFS就是沿着一条路径一直走下去，当遇到终止条件的时候才会返回，而BFS就是先把当前位置附近
的访问一遍，就像下面这样先访问圈内的，然后再把圈放大继续访问，就像下面这样

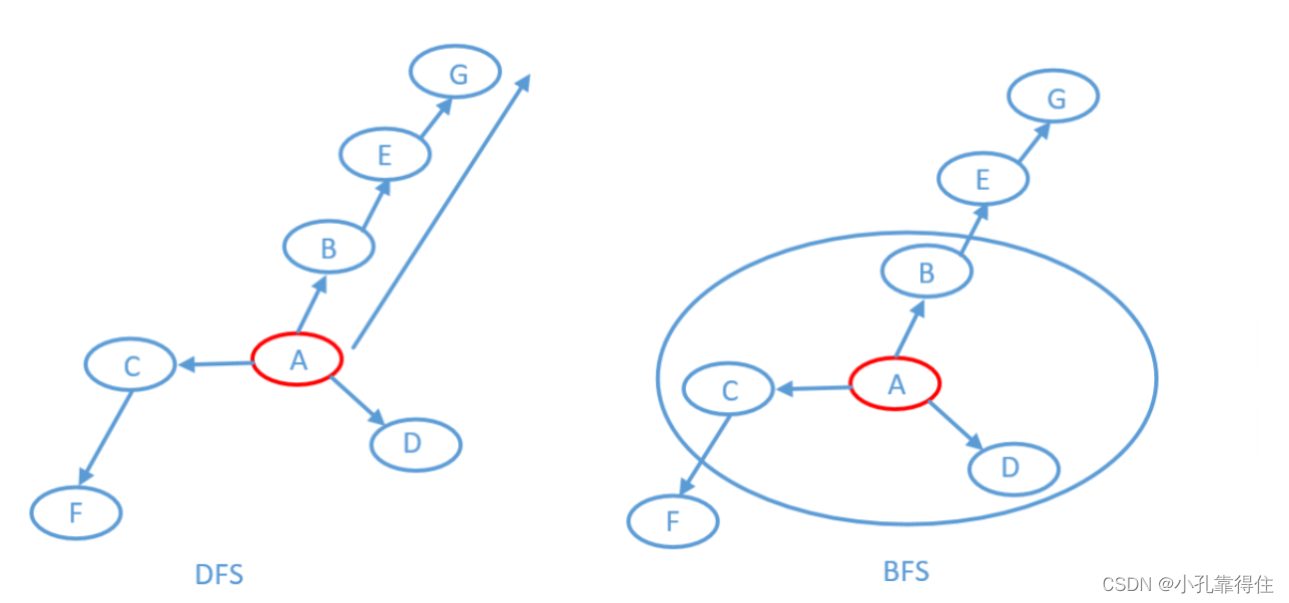
在这里插入图片描述
这题使用BFS和DFS都能解决，如果遇到位置为1的格子，只要能把他们挨着的为1的全部置为0，然后挨着的挨着的为1的位置也置为0，然后…一直这样循环下去，看下代码

public int numIslands(char[][] grid) {
    //边界条件判断
    if (grid == null || grid.length == 0)
        return 0;
    //统计岛屿的个数
    int count = 0;
    //两个for循环遍历每一个格子
    for (int i = 0; i < grid.length; i++)
        for (int j = 0; j < grid[0].length; j++) {
            //只有当前格子是1才开始计算
            if (grid[i][j] == '1') {
                //如果当前格子是1，岛屿的数量加1
                count++;
                //然后通过bfs把当前格子的上下左右4
                //个位置为1的都要置为0，因为他们是连着
                //一起的算一个岛屿，
                bfs(grid, i, j);
            }
        }
    return count;
}

private void bfs(char[][] grid, int x, int y) {
    //把当前格子先置为0
    grid[x][y] = '0';
    int n = grid.length;
    int m = grid[0].length;
    //使用队列，存储的是格子坐标转化的值
    Queue<Integer> queue = new LinkedList<>();
    //我们知道平面坐标是两位数字，但队列中存储的是一位数字，
    //所以这里是把两位数字转化为一位数字
    int code = x * m + y;
    //坐标转化的值存放到队列中
    queue.add(code);
    while (!queue.isEmpty()) {
        //出队
        code = queue.poll();
        //在反转成坐标值（i，j）
        int i = code / m;
        int j = code % m;
        if (i > 0 && grid[i - 1][j] == '1') {//上
            //如果上边格子为1，把它置为0，然后加入到队列中
            //下面同理
            grid[i - 1][j] = '0';
            queue.add((i - 1) * m + j);
        }
        if (i < n - 1 && grid[i + 1][j] == '1') {//下
            grid[i + 1][j] = '0';
            queue.add((i + 1) * m + j);
        }
        if (j > 0 && grid[i][j - 1] == '1') { //左
            grid[i][j - 1] = '0';
            queue.add(i * m + j - 1);
        }
        if (j < m - 1 && grid[i][j + 1] == '1') {//右
            grid[i][j + 1] = '0';
            queue.add(i * m + j + 1);
        }
    }
}