相比于矩阵乘法，floyd巧妙利用了最短路具有最优子结构的性质，即最短路径的子路径也是最短路径，得到以$d_{ij}^{(k)}$（为从i到j的一条中间节点全部取自集合 { 1 , 2 , . . . , k } \{1,2,...,k\} {1,2,...,k}的一条最短路径权重）为状态的转移方程，减少每次迭代的计算量，而且迭代过程只需保存两个矩阵$D^{(k)}$和$D^{(k+1)}$，这也允许我们方便地进行手工验证。

求$D_{ij}^{(k+1)}$时，仅对应floyd算法的一步松弛$D_{ij}^{(k+1)}=min(D_{ij}^{(k)},D_{ik}^{(k)}+D_{kj}^{(k)})$，就是找到前一个矩阵的第$i$行第$k$个元素以及第$j$列第$k$个元素求和和 “十字” 中心元素比大小。

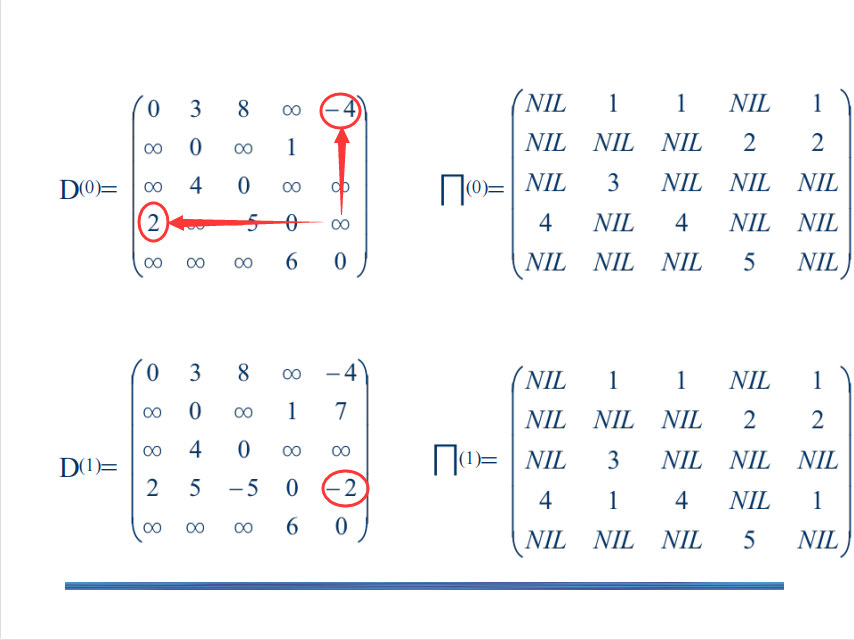
举个例子，如图，$D_{45}^{(1)}$更新为 -2，因为$D_{45}^{(0)}>D_{4k}^{(0)}+D_{k5}^{(0)}$，此时$k=1$，找到$D_{41}^{(0)}$和$D_{15}^{(0)}$.

由于矩阵共有$n^2$个元素，floyd做到了$O(n)$求每个元素，按老师的话说，别人很难想到，因此，前面的矩阵乘法方法叫矩阵乘法求全源最短路，而这个算法用floyd的名字命名。