1. 单词拆分

原题链接

---

题干：

字符串 s 和一个字符串列表 wordDict
利用字典中出现的一个或多个单词拼接出 s 则返回 true

字典中的单词可以重复使用

---

算法原理：

1. 状态表示：

dp[i] 表示： [0, i] 区间内的字符串，能否被字典中的单词拼接而成

2. 状态转移方程

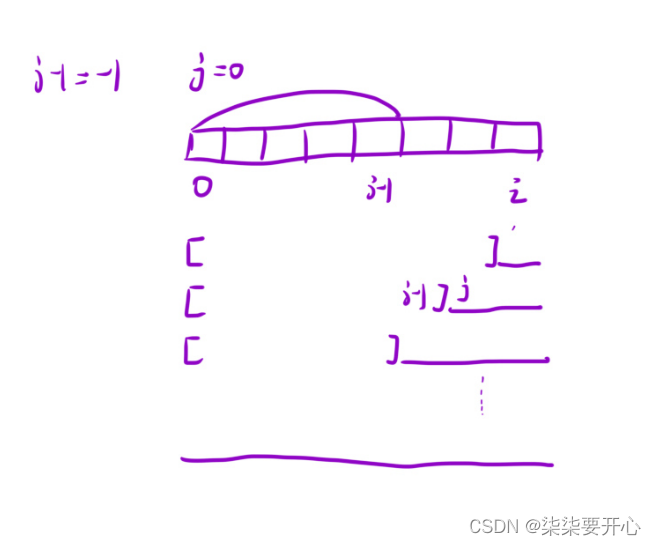
3. 初始化

1. 辅助结点⾥⾯的值要「保证后续填表是正确的」
2. 「下标的映射关系」

dp[0] = true
s = ’ ’ + s

4. 填表顺序

从左往右

5. 返回值

dp[n]

---

代码：

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        //优化：将字典里面的单词存在哈希表里面
        Set<String> hash = new HashSet(wordDict);

        int n = s.length();
        boolean[] dp = new boolean[n + 1];
        dp[0] = true;
        s = " " + s;//处理下标的映射关系

        for(int i = 1; i <= n; i++) {
            for(int j = i; j >= 1; j--) {
                if(dp[j - 1] && hash.contains(s.substring(j, i + 1))) {
                    dp[i] = true;
                    break;
                }
            }
        }
        return dp[n];
    }
}

---

2. 环绕字符串中唯一的子字符串

原题链接

---

题干：

字符串 base 为一个 “abcdefghijklmnopqrstuvwxyz” 无限环绕的字符串

给一个字符串 s ，统计并返回 s 中有多少 不同非空子串 也在base 中出现

---

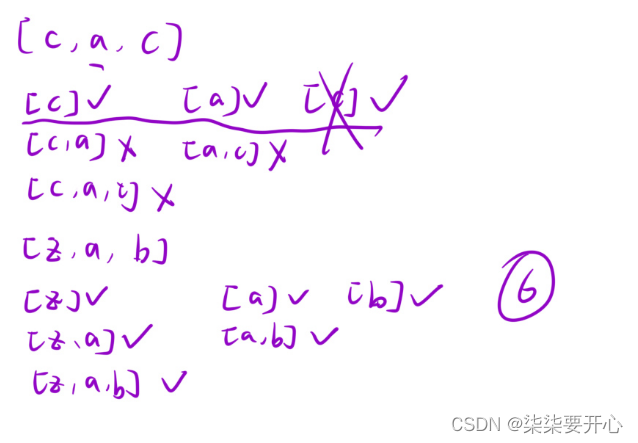
算法原理：

1. 状态表示：

dp[i] 表示：以 i 位置的元素为结尾的所有子串里面，有多少个在 base 中出现过

2. 状态转移方程

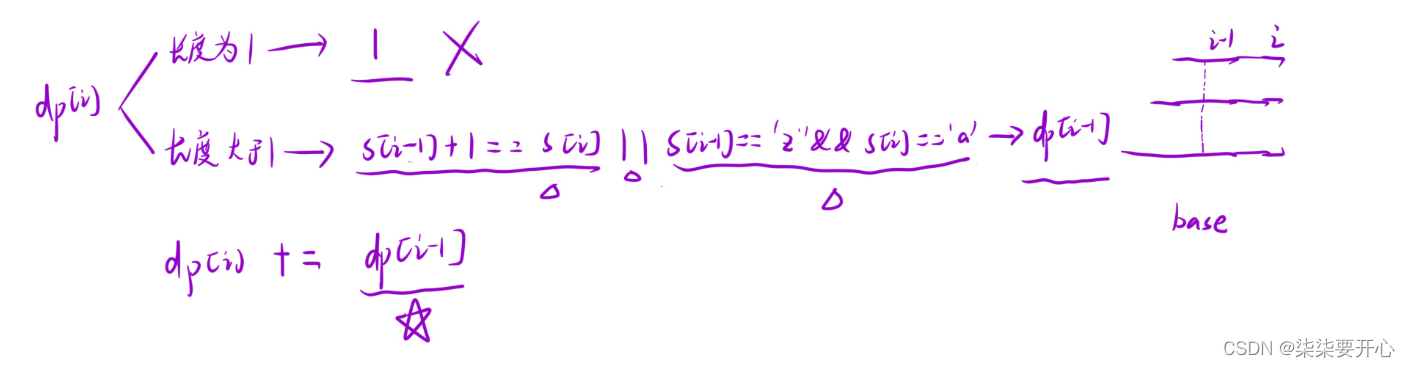
3. 初始化

将表里面的值都初始化为 1

4. 填表顺序

从左往右

5. 返回值

这⾥不能直接返回 dp 表里面的和，因为会有重复的结果。

在返回之前，我们需要先「去重」：

1. 相同字符结尾的 dp 值，我们仅需保留「最大」的即可，其余 dp 值对应的子串都可以在最大的里面找到
2. 可以创建⼀个大小为 26 的数组，统计所有字符结尾的最大 dp 值

最后返回「数组中所有元素的和」即可。

---

代码：

class Solution {
    public int findSubstringInWraproundString(String ss) {
        int n = ss.length();
        char[] s = ss.toCharArray();

        //1. 利用 dp 得到每一个位置为结尾的最长连续数组的长度
        int[] dp = new int[n];
        for(int i = 0; i < n; i++) {
            dp[i] = 1;
        }
        for(int i = 1; i < n; i++) {
            if(s[i - 1] + 1 == s[i] || (s[i - 1] == 'z' && s[i] == 'a')) {
                dp[i] += dp[i - 1];
            }
        }

        //2. 确定返回值
        int[] hash = new int[26];
        for(int i = 0; i < n; i++) {
            hash[s[i] - 'a'] = Math.max(hash[s[i] - 'a'], dp[i]);
        }

        //3. 返回结果
        int sum = 0;
        for(int x : hash) {
            sum += x;
        }
        return sum;
    }
}

3. 计算布尔二叉树的值

原题链接

---

题干：

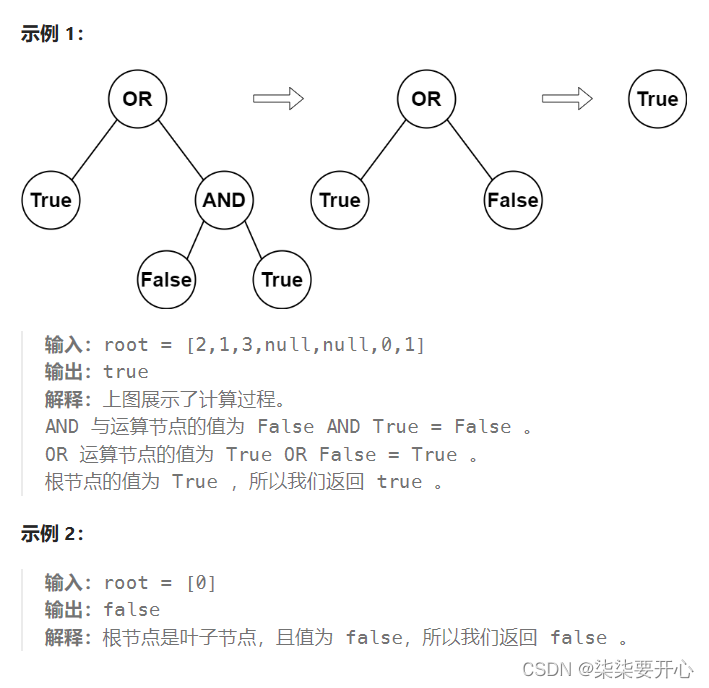
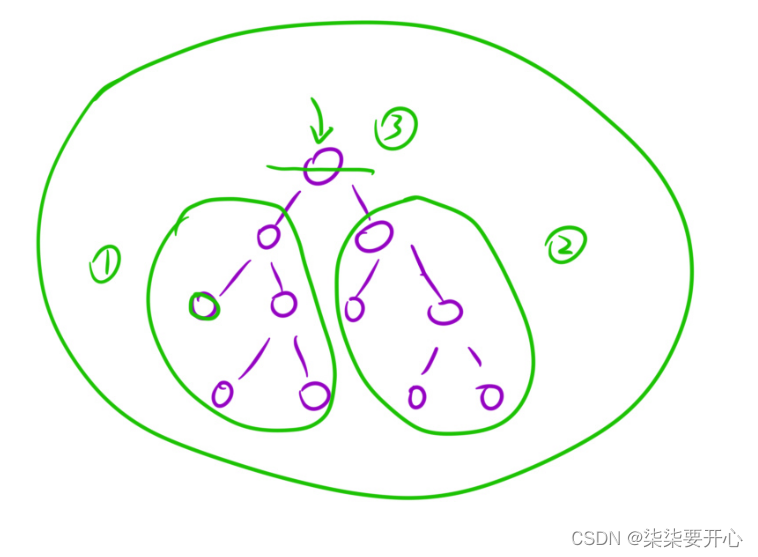
叶子节点 要么值为 0 要么值为 1 ，其中 0 表示 False ，1 表示 True 。

非叶子节点 要么值为 2 要么值为 3 ，其中 2 表示逻辑或 OR ，3 表示逻辑与 AND 。

---

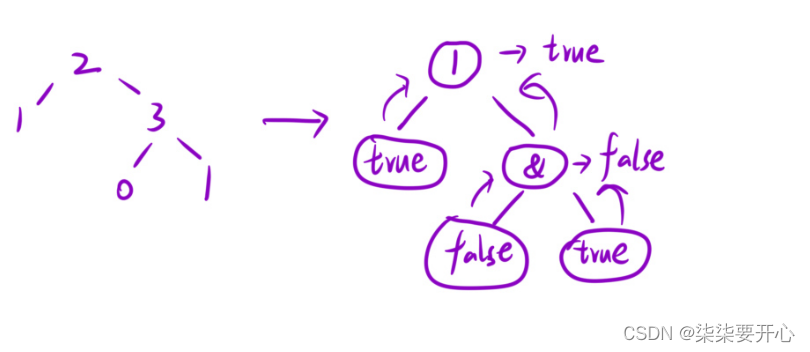
算法原理：

利用递归解决问题

---

代码：

class Solution {
    public boolean evaluateTree(TreeNode root) {
        if(root.left == null) {
            return root.val == 0 ? false : true;
        }
        boolean left = evaluateTree(root.left);
        boolean right = evaluateTree(root.right);
        return root.val == 2 ? left | right : left & right;
    }
}

---

4. 求根节点到叶节点数字之和

原题链接

---

题干：

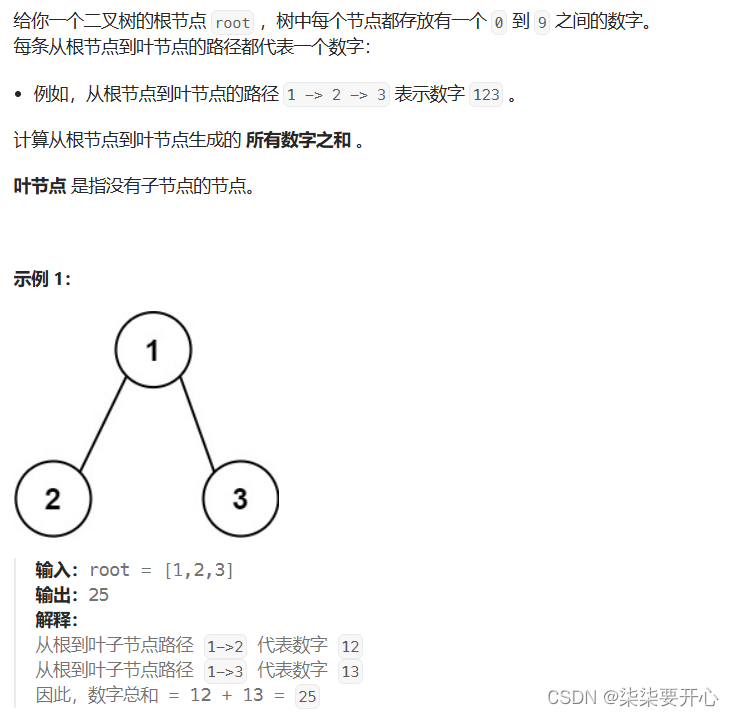
给一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字
每条从根节点到叶节点的路径都代表一个数字

例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123
计算从根节点到叶节点生成的 所有数字之和 。

---

算法原理：

使用递归解决问题

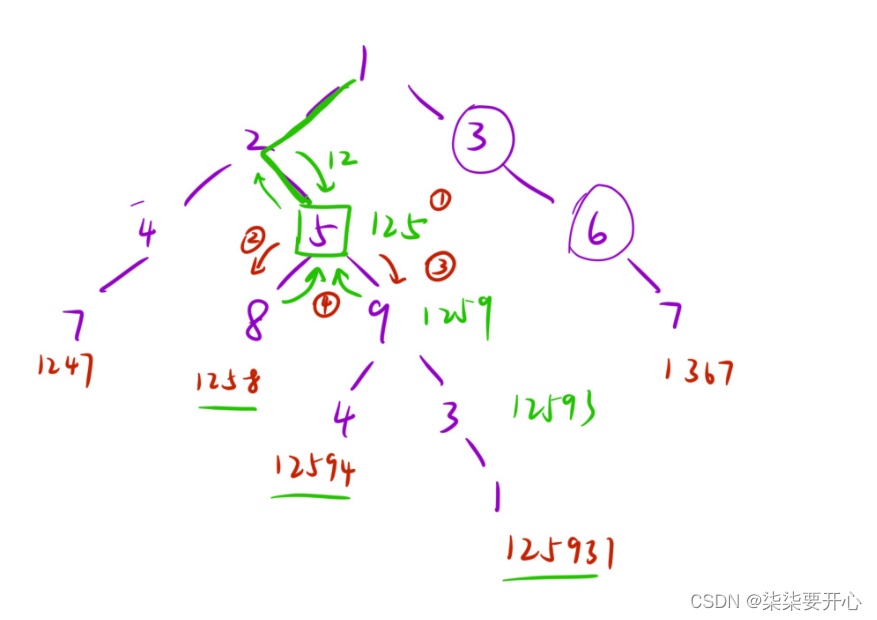
1. 函数头
   int dfs(TreeNode* root, int preSum)
2. 函数体
   ① ② ③ ④
3. 递归出口
   叶子结点

---

代码：

class Solution {
    public int sumNumbers(TreeNode root) {
        return dfs(root, 0);
    }

    public int dfs(TreeNode root, int preSum) {
        preSum = preSum * 10 + root.val;
        if(root.left == null && root.right == null) {
            return preSum;
        }

        int ret = 0;
        if(root.left != null) {
            ret += dfs(root.left, preSum);
        }
        if(root.right != null) {
            ret += dfs(root.right, preSum);
        }
        return ret;
    }
}