二叉树的遍历
1. 二叉树的前序、中序、后序遍历
- 前、中、后序遍历又叫深度优先遍历
- 注:严格来说,深度优先遍历是先访问当前节点再继续递归访问,因此,只有前序遍历是严格意义上的深度优先遍历
- 首先需要知道下面几点:
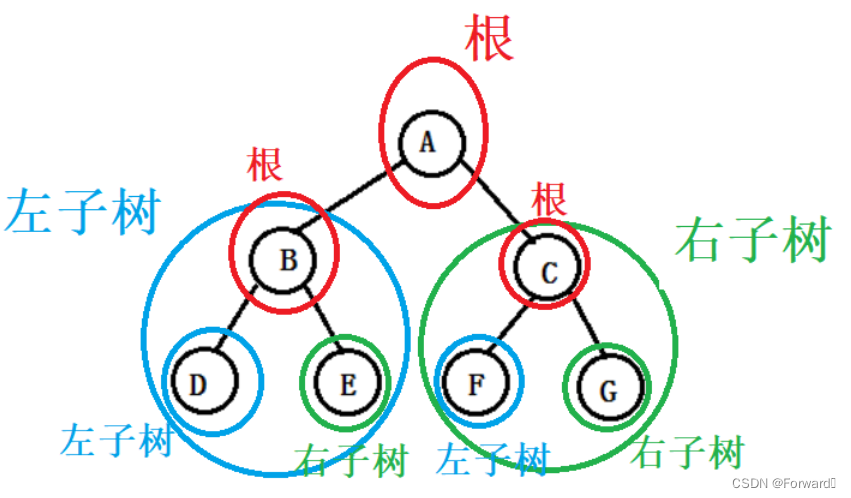
- 任何一颗二叉树,都由根节点、左子树、右子树构成。
如图:
- 分治算法:分而治之。大问题分成类似的子问题,子问题再分成子问题……直到子问题不能再分割。对树也可以做类似的处理,对一棵树不断地分割,直到子树为空时,分割停止。
- 关于二叉树的许多问题我们都要利用分治思想,将一棵完整的树分解成根和左右两棵子树,然后再对这两棵子树进行相同的递归处理,最后得到结果。
- 如果对递归的过程想的不太清楚,建议画递归展开图来辅助理解。
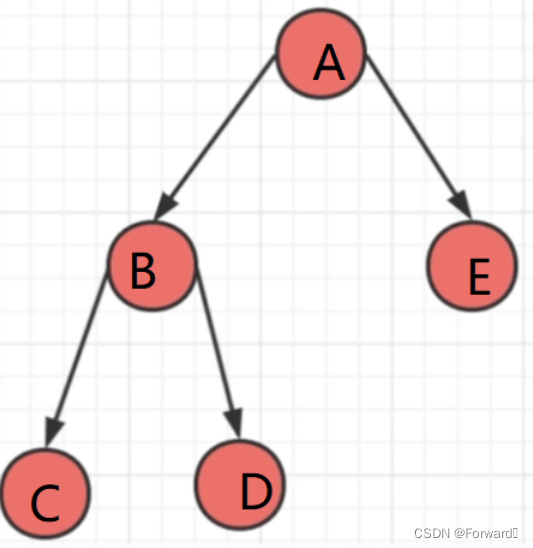
1.1 前序(先根)遍历
-
遍历顺序:根- > 左子树 -> 右子树(即先访问根,再访问左子树,最后在访问右子树)
-
如上图中:A -> B -> C -> NULL -> NULL -> D -> NULL -> NULL -> E -> NULL -> NULL
typedef char BTDataType;
typedef struct BinaryTreeNode
{
struct BinaryTreeNode *left; //指向左子树
struct BinaryTreeNode *right; //指向右子树
BTDataType data;
}BTNode;
void PrevOrder(BTNode * root) //前序遍历
{
if (!root)
return;
printf("%d ",root->data); //根
PrevOrder(root->left); //左子树
PrevOrder(root->right); //右子树
return;
}
递归顺序图:
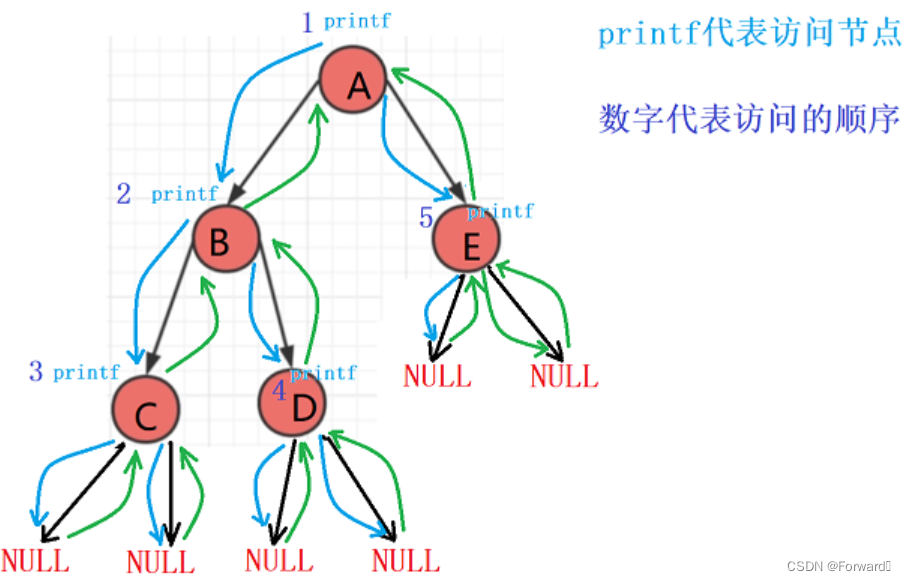
递归展开图:

1.2 中序(中根)遍历
-
遍历顺序:左子树 -> 根 -> 右子树(即先访问左子树,再访问根,最后在访问右子树)
-
如上图中:NULL -> C -> NULL -> B -> NULL -> D -> NULL -> A -> NULL -> E -> NULL
void InOrder(BTNode* root)
{
if (!root)
return;
InOrder(root->left); //左子树
printf("%c ", root->data); //根
InOrder(root->right); //右子树
return;
}
递归顺序图:
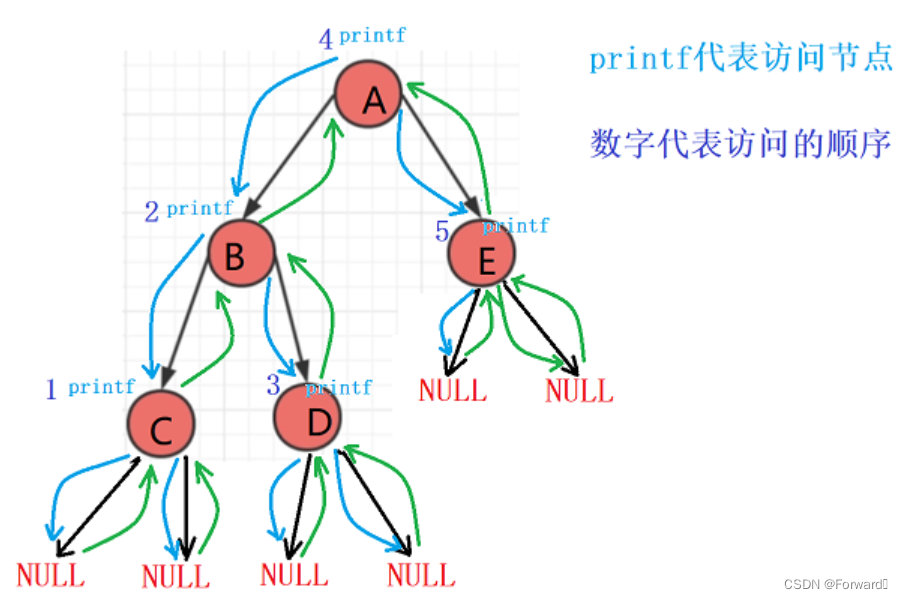
1.3 后序(后根)遍历
-
遍历顺序:左子树 -> 右子树 -> 根(即先访问左子树,再访问左=右子树,最后在访问根)
-
如上图中:NULL -> NULL -> C -> NULL -> NULL -> D -> B -> NULL -> NULL -> E -> A
void PostOrder(BTNode* root)
{
if (!root)
{
printf("NULL ");
return;
}
PostOrder(root->left); //左子树
PostOrder(root->right); //右子树
printf("%c ", root->data); //根
}
递归顺序图:
2. 二叉树前中后序的非递归遍历
- 在利用递归来进行二叉树的前中后序遍历时,我们通常将一棵二叉树看成三部分:根、左子树、右子树。
- 但是对于前中后序的非递归遍历,我们需要转变思路:应当将一棵二叉树看成两部分:左路节点、左路节点的右子树
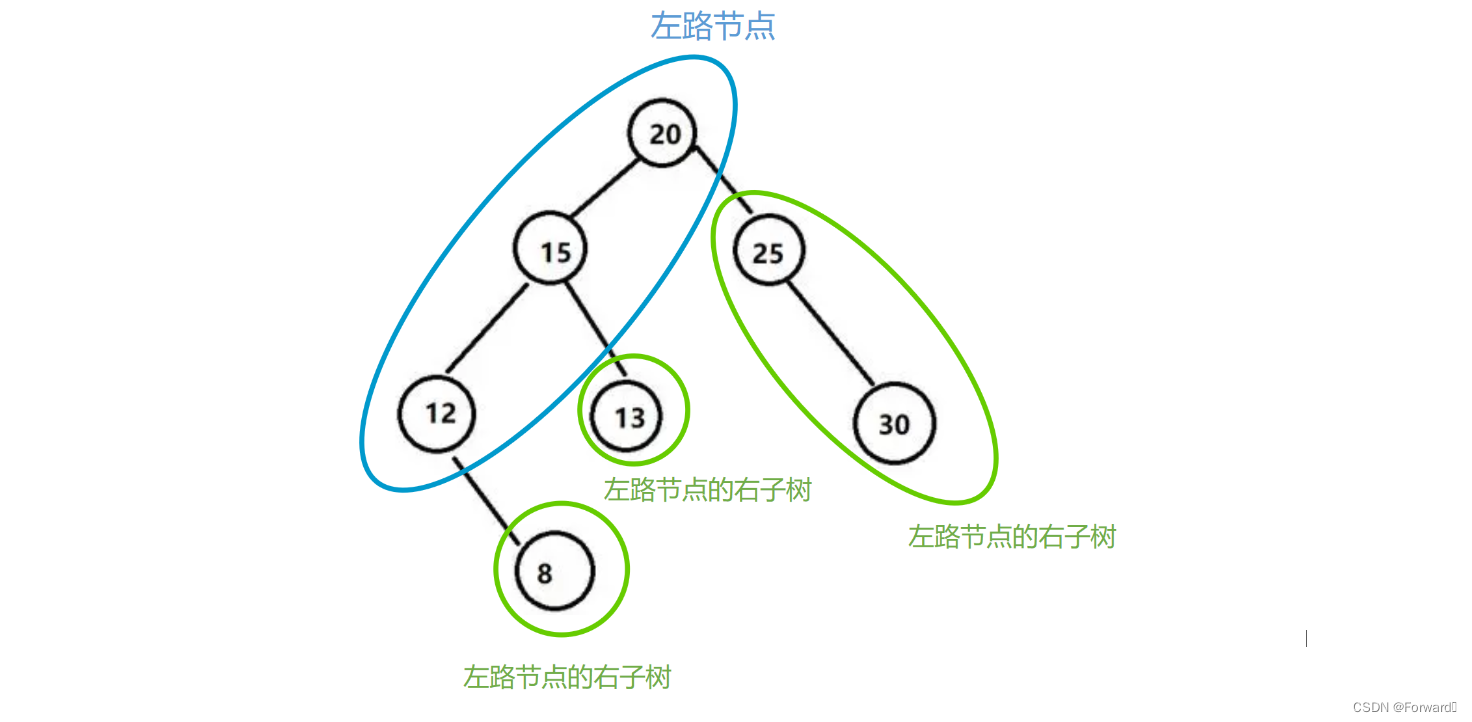
2.1 前序非递归
前序遍历的顺序是:根 -> 左子树 -> 右子树。
具体到一棵二叉树,就是自顶向下将左路节点遍历完,再自底向上遍历左路节点的右子树。如图:
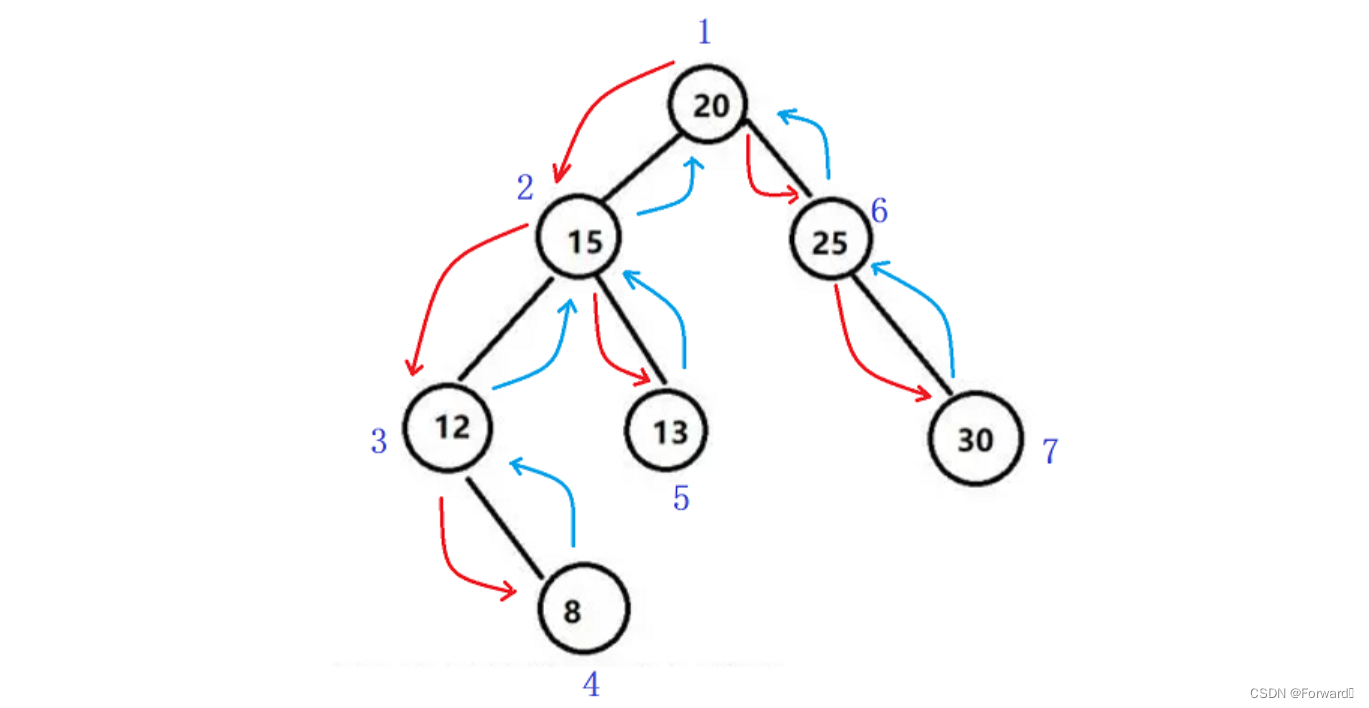
为了能够在遍历完左路节点后还能得到这个节点从而得到这个节点的右子树,我们需要利用栈来对左路节点进行存储。
实现代码:
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> ret;
stack<TreeNode*> st;
TreeNode* cur = root;
while (cur || !st.empty())
{
//遍历左路节点,将左路节点的值打印的同时将节点入栈
while (cur)
{
ret.push_back(cur->val);
st.push(cur);
cur = cur->left;
}
TreeNode* tmp = st.top();
st.pop();
//此时cur即为左路节点的右子树
//将这棵右子树看成一颗完整的二叉树,进行相同的操作
cur = tmp->right;
}
return ret;
}
};
2.2 中序非递归
中序遍历的顺序是:左子树 -> 根 -> 右子树
具体到一棵二叉树,即从左路节点的最深处开始,先遍历这个节点,再遍历这个节点的右子树,自底向上。
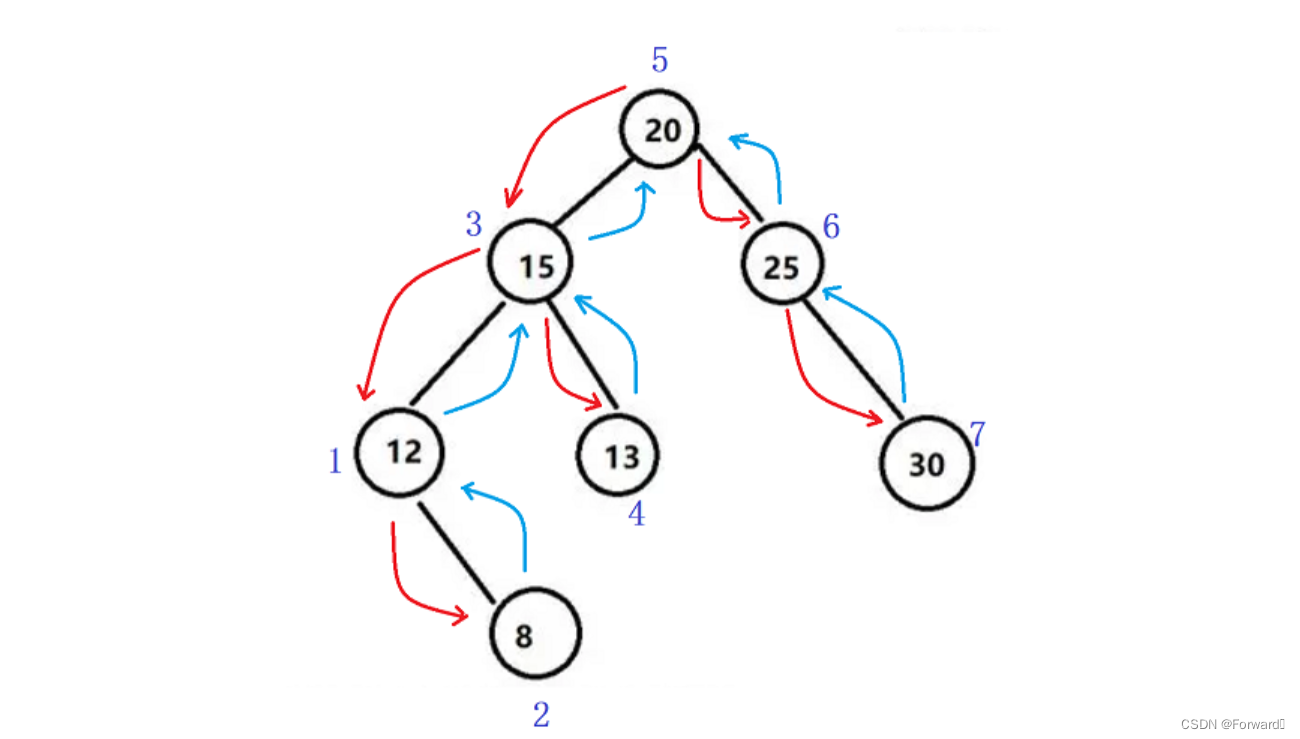
同样,为了能够找到之前的左路节点,也需要一个栈来对左路节点进行保存
实现代码:
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> ret;
stack<TreeNode*> st;
TreeNode* cur = root;
while (cur || !st.empty())
{
//遍历左路节点的时候将左路节点入栈
//由于左子树先于根,因此先不要打印左路节点(根)的值
while (cur)
{
st.push(cur);
cur = cur->left;
}
//程序第一次走到这里时,tmp就是左路节点的最深处
//tmp的左子树为nullptr(或已经遍历完tmp的左子树),因此打印其(根)值
TreeNode* tmp = st.top();
st.pop();
ret.push_back(tmp->val);
//遍历左路节点的右子树
cur = tmp->right;
}
return ret;
}
};
2.3 后序非递归
后序的遍历顺序为:左子树 -> 右子树 -> 根
具体到一棵二叉树,即从左路节点的最深处开始,先遍历左路节点的右子树,再遍历左路节点,自底向上。如图:
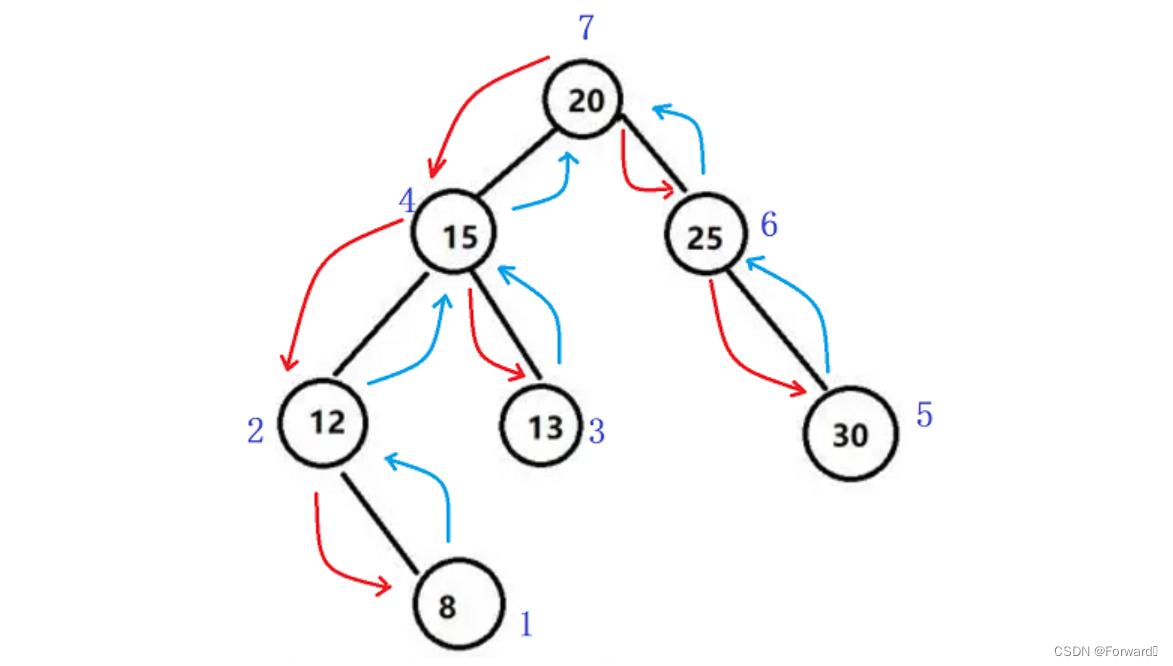
同样,也需要一个栈来保存之前的左路节点
此外,由于后序遍历的顺序为:左子树 -> 右子树 -> 根,需要遍历完根(左路节点)的左子树和右子树后才能对其值进行打印,在这个过程中,我们会经过两次根,且只能在第二次经过根时才能打印根的值,为了确保我们打印根的时机,可以利用一个指针prev来记录之前遍历的位置:如果prev停留在左路节点的右子树的根节点,就说明此时左右子树已经遍历完,可以打印根的值
实现代码:
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> ret;
stack<TreeNode*> st;
TreeNode* cur = root;
TreeNode* prev = nullptr;
while (cur || !st.empty())
{
//将左路节点入栈
while (cur)
{
st.push(cur);
cur = cur->left;
}
TreeNode* tmp = st.top();
//如果左路节点的右子树为空或者prev停留在右子树的根
//说明根的左子树和右子树都已遍历完
//打印根值(遍历根),同时跟新prev的位置
if (tmp->right == nullptr || prev == tmp->right)
{
ret.push_back(tmp->val);
st.pop();
prev = tmp;
}
else //否则,说明根的右子树没有遍历完,遍历右子树
cur = tmp->right;
}
return ret;
}
};
2. 二叉树的层序遍历
-
层序遍历又叫广度优先遍历。
-
设二叉树的根节点所在层数为1,层序遍历就是从根节点出发,首先访问第一层的节点,然后从左到右访问第二层上的节点,接着访问第三层的节点,以此类推,自上而下,自左往右逐层访问树的结点的过程就是层序遍历。
-
层序遍历借助队列的先进先出思想来实现。
-
核心思想:上一层带下一层
-
如图就是对上面那棵树的层序遍历示意图:

-
实现代码
typedef BTNode* QDataType; //队列元素类型
typedef struct QueueNode
{
struct QueueNode* next;
QDataType data;
}QueueNode;
typedef struct Queue //定义存放指向队头,队尾指针的结构体
{
QueueNode* head; //指向队头
QueueNode* tail; //指向队尾
}Queue;
//层序遍历
void LevelOrder(BTNode* root)
{
Queue *q = (Queue *)malloc(sizeof(Queue)); //创建队列
QueueInit(q); //初始化队列
//如果根节点为空,直接退出函数
if (!root)
return;
QueuePush(q, root); //先将根节点入队入队
while (!QueueEmpty(q)) //当队列不为空
{
BTNode* front = QueueFront(q); //接收队头元素
QueuePop(q); //出队头元素
printf("%c ", front->data); //访问该节点
if (front->left) //如果左子树不为空
QueuePush(q, front->left); //左子树入队
if (front->right) //如果右子树不为空
QueuePush(q, front->right); //右子树入队
}
printf("\n");
QueueDestroy(q); //销毁队列
}
3. 二叉树遍历的应用

- 由二叉树和层序遍历的思想,我们可以构造出这棵树
- 再有前序遍历 根- > 左子树 -> 右子树 的思想,可以知道,这棵树的前序序列为:A B D H E C F G

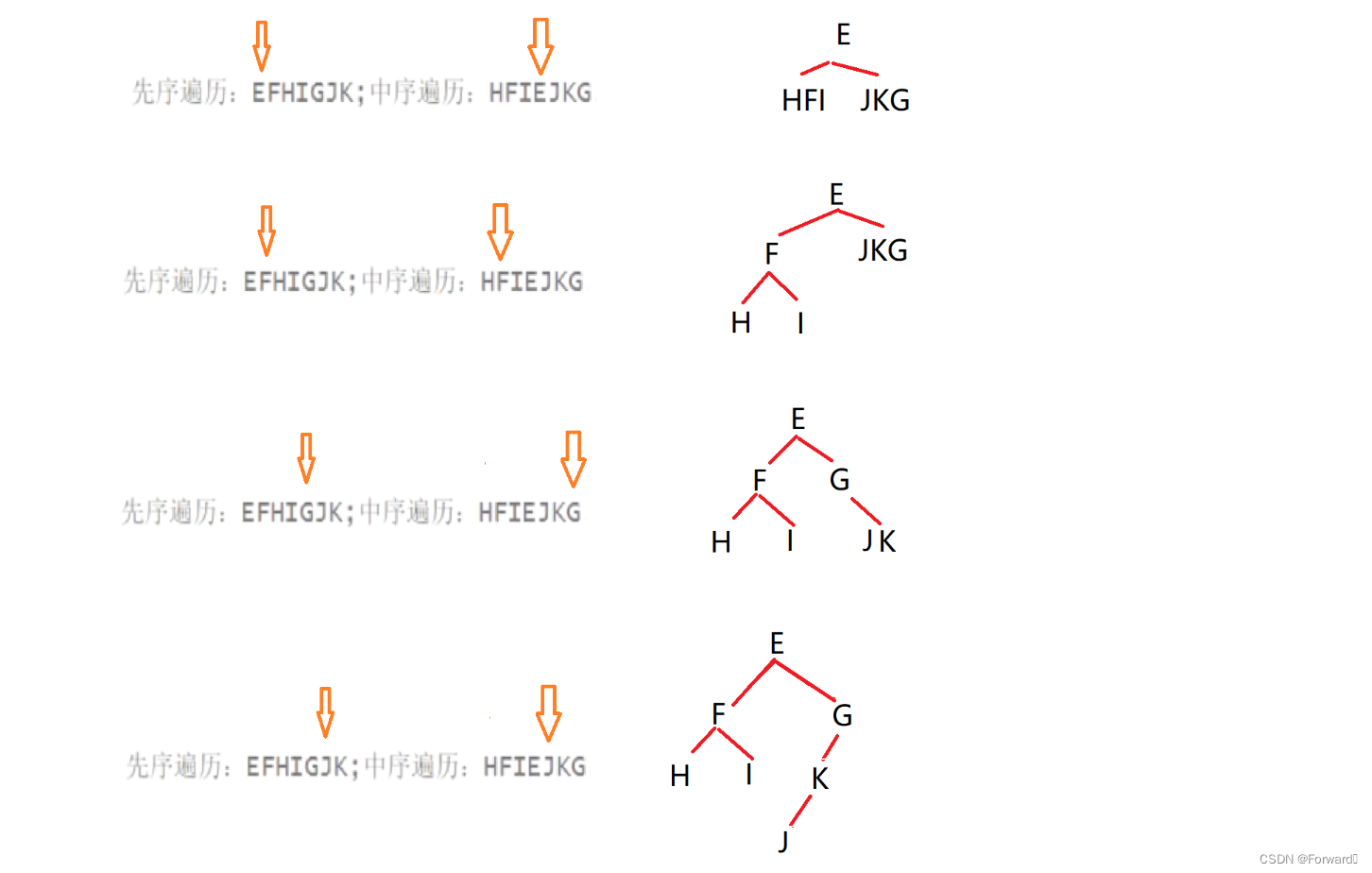
- 这道题是由二叉树的前序序列和中序序列来确定二叉树,我们知道中序遍历的思想是 左子树 -> 根 -> 右子树 ,根将左子树和右子树分割开来,那么我们就可以先用前序序列确定根,再用中序序列确定根的左右子树,这样就可以将这棵二叉树确定了,如图:
- 显然根节点为E
我们同样可以用代码,利用一棵二叉树的前序序列和中序序列来将这棵二叉树还原👉Leetcode -> 从前序与中序遍历序列构造二叉树
class Solution { public: //前序序列即为根序列 //在中序序列找到根后可以将序列分为左右两部分,这两部分分别就是跟的左子树序列和右子树序列 TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder, int& prei, int inBegin, int inEnd) { //区间长度小于1,直接返回空 if (inBegin > inEnd) return nullptr; //前序序列即为根序列 TreeNode* root = new TreeNode(preorder[prei++]); //在中序序列中找到根 int pos = 0; while (1) { if (root->val != inorder[pos]) pos++; else break; } //分别前往左子树和右子树进行连接 root->left = _buildTree(preorder, inorder, prei, inBegin, pos - 1); root->right = _buildTree(preorder, inorder, prei, pos + 1, inEnd); return root; } TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) { int i = 0; TreeNode* root = _buildTree(preorder, inorder, i, 0, inorder.size() - 1); return root; } };

- 这题和第二题类似,同样是先由后序遍历(左子树 -> 右子树 -> 根)确定根节点,再由中序遍历确定根的左右子树,只是用后序遍历确定根节点时要从最后开始。如图:
易得前序遍历为a b c d e
我们同样可以用代码,利用一棵二叉树的前序序列和中序序列来将这棵二叉树还原👉Leetcode -> 从中序与后序遍历序列构造二叉树
class Solution { public: //思想同前序序列和中序序列确定二叉树类似 TreeNode* _buildTree(vector<int>& inorder, vector<int>& postorder, int& posi, int inBegin, int inEnd) { if (inBegin > inEnd) return nullptr; TreeNode* root = new TreeNode(postorder[posi--]); int pos = 0; while (1) { if (root->val != inorder[pos]) pos++; else break; } root->right = _buildTree(inorder, postorder, posi, pos + 1, inEnd); root->left = _buildTree(inorder, postorder, posi, inBegin, pos - 1); return root; } TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) { int i = postorder.size() - 1; TreeNode* root = _buildTree(inorder, postorder, i, 0, inorder.size() - 1); return root; } };
总结:
由于二叉树的中序遍历可以分割二叉树的左右节点,因此 前序序列 + 中序序列 / 后序序列 + 中序序列 都可以构建出一棵二叉树,而单独序列和 前序序列 + 后序序列就不行。
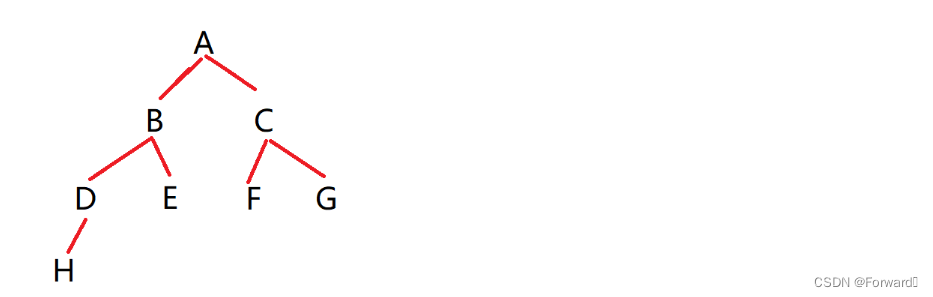





![docker ENTRYPOINT [“sh“,“-c“,“java“,“-jar“,“Hello.jar“] 启动失败问题分析](https://img-blog.csdnimg.cn/direct/5a78147afc9a46f7b3ddb5fabeb33b20.png)