话不多说,直接看题:
1.换根DP:
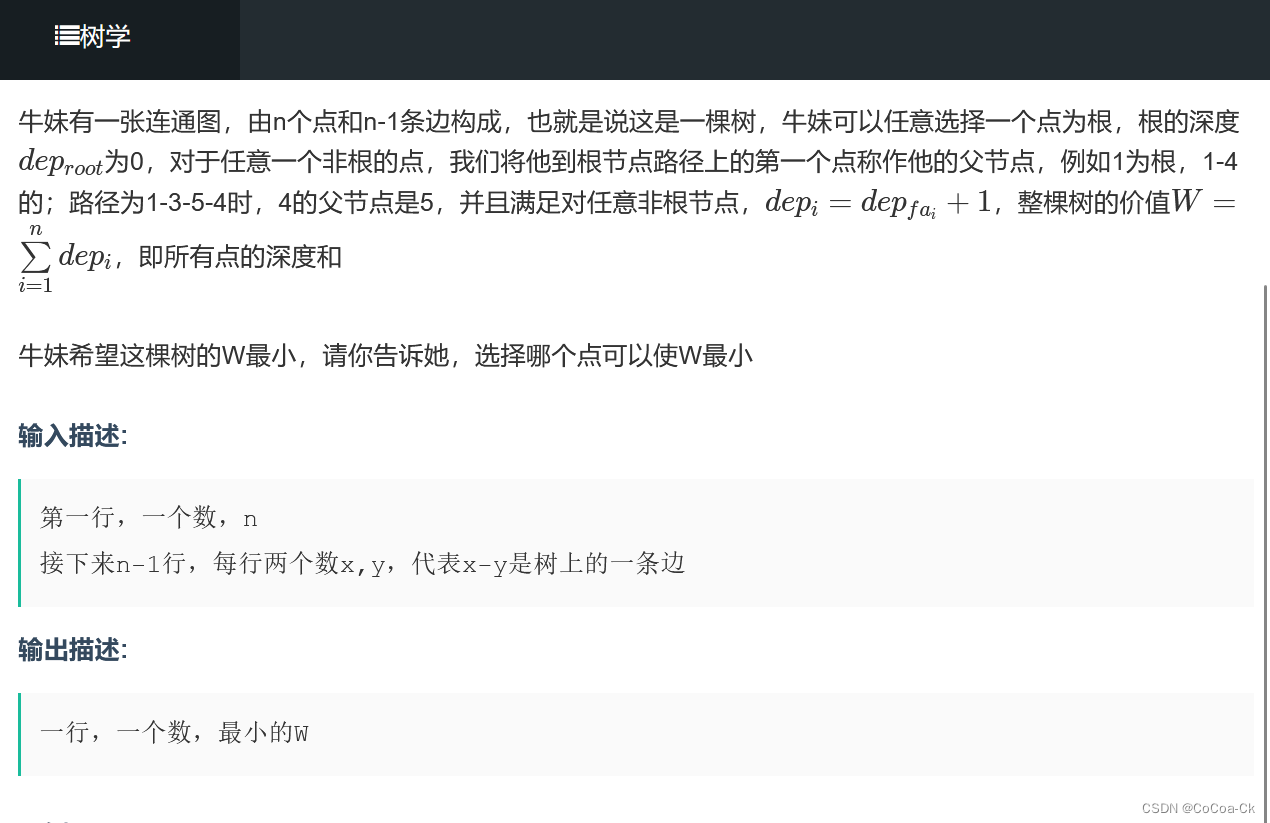
我们肯定不能对每一个根节点暴力求,我们不妨先求f[1],我们发现当他的儿子作为根节点时深度和为f[1]+(n-cnt[i])-cnt[i](cnt[i]表示以i为根的节点数),这样子两遍DFS即可,下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,x,y,cnt[1000020],dep[1000010];
long long f[1000010];
vector<int> edge[1000010];
void dfs1(int root,int fa){
cnt[root]=1;
for(int i=0;i<edge[root].size();i++){
int w=edge[root][i];
if(w==fa) continue;
dep[w]=dep[root]+1;
dfs1(w,root);
cnt[root]+=cnt[w];
}
return;
}
void dfs2(int root,int fa){
for(int i=0;i<edge[root].size();i++){
int w=edge[root][i];
if(w==fa) continue;
f[w]=f[root]+n-2*cnt[w];
dfs2(w,root);
}
return;
}
int main(){
cin>>n;
for(int i=1;i<=n-1;i++){
scanf("%d%d",&x,&y);
edge[x].push_back(y);
edge[y].push_back(x);
}
dep[1]=0;
dfs1(1,0);
for(int i=1;i<=n;i++){
f[1]+=dep[i];
}
dfs2(1,0);
long long ans=f[1];
for(int i=2;i<=n;i++){
ans=min(ans,f[i]);
}
cout<<ans;
}2.数学问题的背包转化:
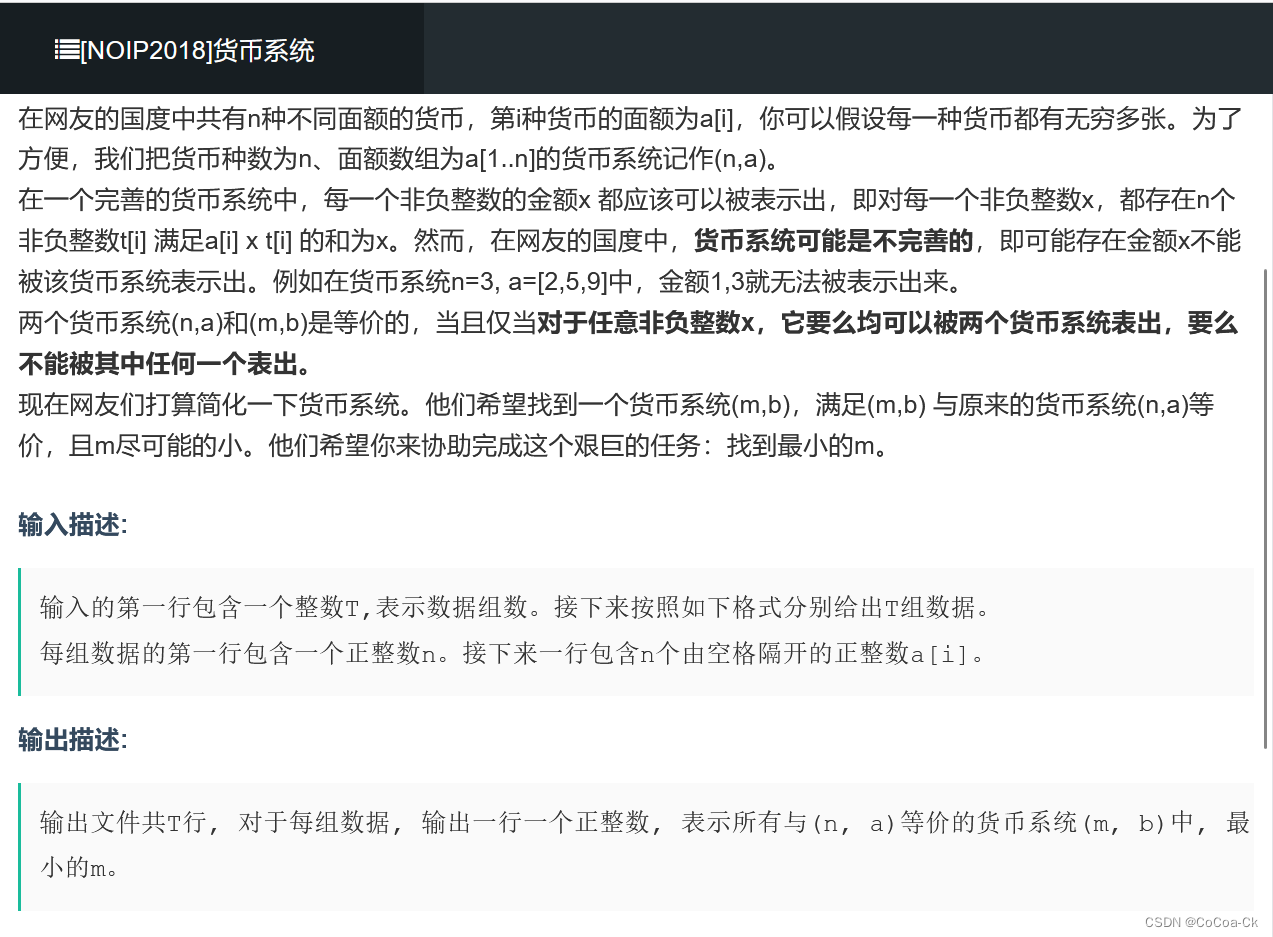
显然,我们要求的就是n个中的极大线性无关组,那么我们如何求?
只要一个数可以被比他小的组合表示出来,那么这个元素就可以删了。
如何实现?我们把每一个元素看成无穷个物品,我们判断一个元素是否可以被表示,就是看这个背包是否可以被塞满,因此变成了完全背包问题,下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int a[110],n,t,m;
bool dp[25005];
bool cmp(int a,int b){
return a<b;
}
int main(){
cin>>t;
while(t--){
cin>>n;
memset(dp,0,sizeof(dp));
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
sort(a+1,a+n+1,cmp);
m=n;
dp[0]=1;
for(int i=1;i<=n;i++){
if(dp[a[i]]==1){
m--;
continue;
}
for(int j=a[i];j<=a[n];j++){
dp[j]=dp[j-a[i]]||dp[j];
}
}
cout<<m<<endl;
}
}3.水题记录位置

就是在中序遍历上找根,再变成两个区间,用区间DP即可。
那么我们如何记录前序遍历呢,直接放在一维数组实现起来比较麻烦,于是我们可以用root[i][j]来记录i--j中选的根,然后再递归下去即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int dp[40][40],n,a[40],root[40][40];
int f(int l,int r){
if(dp[l][r]>0) return dp[l][r];
if(l==r) return dp[r][r]=a[r];
if(l>r) return 1;
int g=l;
for(int i=l;i<=r;i++){
if(dp[l][r]<=a[i]+f(l,i-1)*f(i+1,r)){
dp[l][r]=a[i]+f(l,i-1)*f(i+1,r);
g=i;}
}
root[l][r]=g;
return dp[l][r];
}
void print(int l,int r){
if(l==r){
cout<<l<<" ";
return;
}
if(l>r) return;
cout<<root[l][r]<<" ";
print(l,root[l][r]-1);
print(root[l][r]+1,r);
return;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
cout<<f(1,n)<<endl;
print(1,n);
}4.从小入手+两遍DP:

我们不妨先看一块,我们令f[k][i][x]表示第k条木板,前x个格子刷i次的最大正确粉刷格子数。
对于第k条木板,易得转移方程:f[k][i][x]=max(f[k][i-1][p]+w[p+1][x])(w[i][j]表示i--j一次刷最多可以刷对的格子数)
这样子,我们就把每一条木板刷的所有情况求出来,问题就转化成了分组背包。
我们令g[i][j]表示前i个木板刷了j次正确格子。
g[i][j]=g[i-1][k]+f[i][j-k][m].
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,t,a[60][60],f[55][2600][55],g[55][2600],ck0[55][55],ck1[55][55],ff[55][2600];
char x;
int main(){
cin>>n>>m>>t;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
scanf(" %c",&x);
a[i][j]=x-'0';
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(a[i][j]==0){
ck0[i][j]=ck0[i][j-1]+1;
ck1[i][j]=ck1[i][j-1];
}
else{
ck1[i][j]=ck1[i][j-1]+1;
ck0[i][j]=ck0[i][j-1];
}
}
}
int x1,x2;
for(int i=1;i<=n;i++){
for(int j=1;j<=t;j++){
for(int k=1;k<=m;k++){
for(int p=0;p<=k;p++){
x1=ck0[i][k]-ck0[i][p];
x2=ck1[i][k]-ck1[i][p];
f[i][j][k]=max(f[i][j][k],f[i][j-1][p]+max(x1,x2));
}
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=t;j++){
for(int k=0;k<=j;k++){
g[i][j]=max(g[i][j],f[i][k][m]+g[i-1][j-k]);
}
}
}
cout<<g[n][t];
}