【题目描述】
请利用链式前向星存图，编程输出无向无权图各个顶点的度。

【输入样例】
5 6
1 3
2 1
1 4
2 3
3 4
5 1

【输出样例】
4
2
3
2
1

【算法分析】
本例需要用到基于链式前向星的广度优先搜索（BFS）。
链式前向星广度优先搜索（BFS）参见：https://blog.csdn.net/hnjzsyjyj/article/details/119917795

本题给出的测试样例对应的示意图如下：

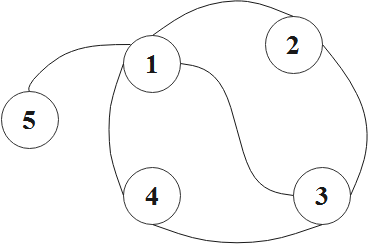
【算法代码】

/* 链式前向星存图
val[idx] 表示第 idx 条边的权值。
e[idx] 表示第 idx 条边的终点。
ne[idx] 表示与第 idx 条边同起点的最近一次被添加的边的编号。
h[a] 表示以结点 a 为起点的最近一次被添加的边的编号。这个表述是在使用 ne[idx]=h[a] 时，也即使用 h[a]=idx++ 更新 h[a] 之前而言的。要特别注意这个语境。
*/
 
#include <bits/stdc++.h>
using namespace std;
 
const int N=1e5+5;
const int M=N<<1;
int n,m;
int h[N],e[M],ne[M],idx;
bool st[N];
 
int ans;
 
void add(int a,int b) {
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
 
void bfs(int u) {
    queue<int>q;
    st[u]=true;
    q.push(u);
    while(!q.empty()) {
        int cnt=0;
        int t=q.front();
        q.pop();
        for(int i=h[t]; ~i; i=ne[i]) { //~i; equivalent to i!=-1;
            cnt++;
            int j=e[i];
            if(!st[j]) {
                q.push(j);
                st[j]=true; //need to be flagged immediately after being queued
            }
        }
        cout<<cnt<<endl;
        break;
    }
}
 
int main() {
    cin>>n>>m;
    memset(h,-1,sizeof(h));
    for(int i=1; i<=m; i++) {
        int a,b;
        cin>>a>>b;
        add(a,b),add(b,a); //undirected graph
    }
 
    for(int i=1;i<=n;i++){
        memset(st,false,sizeof(st));
        bfs(i); //bfs(i),i is node's name from 1
    }
 
    return 0;
}


/*
in:
5 6
1 3
2 1
1 4
2 3
3 4
5 1

out:
4
2
3
2
1
*/

【参考文献】
https://blog.csdn.net/hnjzsyjyj/article/details/119917795
https://blog.csdn.net/hnjzsyjyj/article/details/119938620
https://blog.csdn.net/hnjzsyjyj/article/details/119912125