一篇数据浓缩在医疗数据集应用中的论文。
其实就是在医疗数据集上使用了data condensation的方法，这里使用了DM的方式，并且新增了浓缩时候使用不同的网络。

1. 方法

数据浓缩DC的目的是：
$${\mathbb{E}}_{\mathbf{x}\sim P_{\mathcal{D}}}\left[\mathrm{L}\left({\phi }_{{\mathbf{\theta }}^{\mathcal{O}}}(\mathbf{x}),y\right)\right]\simeq {\mathbb{E}}_{\mathbf{x}\sim P_{\mathcal{D}}}\left[\mathrm{L}\left({\phi }_{{\mathbf{\theta }}^c}(\mathbf{x}),y\right)\right]$$
对于数据x，在原始数据$\mathcal{O}$和生成数据$c$上训练得到的模型要有接近的模型效果。
作者用DM来实现数据浓缩，并且选择随机的模型，随机的参数（作者说在DM中，只选择了一个模型的而不同参数训练，这里使用不同模型不同参数更能保护隐私）
$$\underset{\mathcal{C}}{\min }{\mathbb{E}}_{{\varphi }_{{\mathbf{\mu }}_k}^k\sim \Phi ,{\mathbf{\mu }}_k\sim P_{{\mathbf{\mu }}_k}}{\Vert \frac{1}{|\mathcal{O}|}\sum _{i=1}^{|\mathcal{O}|}{\varphi }_{{\mathbf{\mu }}_k}^k\left({\mathbf{x}}_i\right)-\frac{1}{|\mathcal{C}|}\sum _{j=1}^{|\mathcal{C}|}{\varphi }_{{\mathbf{\mu }}_k}^k\left({\mathbf{c}}_j\right)\Vert }^2$$

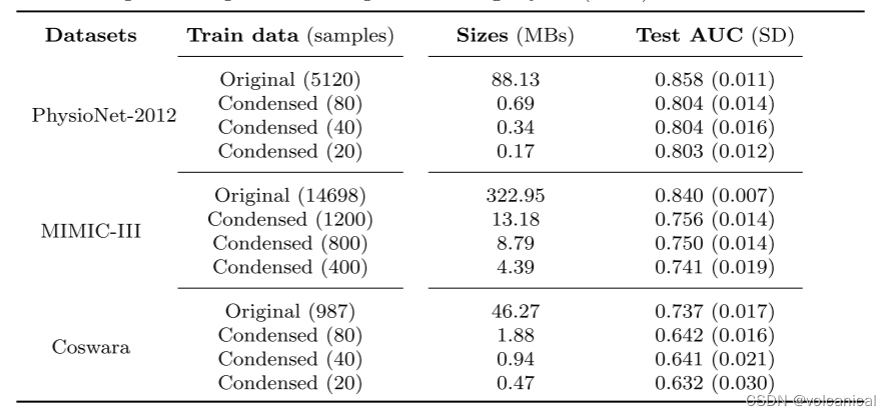
2. 结果：