#include <stdio.h>
#define MAX_N 1003
int a[MAX_N][MAX_N], d[MAX_N][MAX_N];
// 差分数组的初始化
void init_diff(int n, int m) {
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            d[i][j] = a[i][j] - a[i-1][j] - a[i][j-1] + a[i-1][j-1];
        }
    }
}
// 对差分数组进行区间更新
void update_diff(int x1, int y1, int x2, int y2, int c) {
    d[x1][y1] += c;
    d[x1][y2+1] -= c;
    d[x2+1][y1] -= c;
    d[x2+1][y2+1] += c;
}
int main() {
    int n, m, q;
    scanf("%d %d %d", &n, &m, &q);
    // 输入初始的球筐矩阵
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            scanf("%d", &a[i][j]);
        }
    }
    // 初始化差分数组
    init_diff(n, m);
    // 处理每次操作
    while (q--) {
        int x1, y1, x2, y2, c;
        scanf("%d %d %d %d %d", &x1, &y1, &x2, &y2, &c);
        update_diff(x1, y1, x2, y2, c);
    }
    // 通过差分数组还原最终的球筐矩阵
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            // 累加从(1,1)到(i,j)的差分和来还原a[i][j]
            d[i][j] += d[i-1][j] + d[i][j-1] - d[i-1][j-1];
            printf("%d ", d[i][j]);
        }
        printf("\n");
    }
    return 0;
}

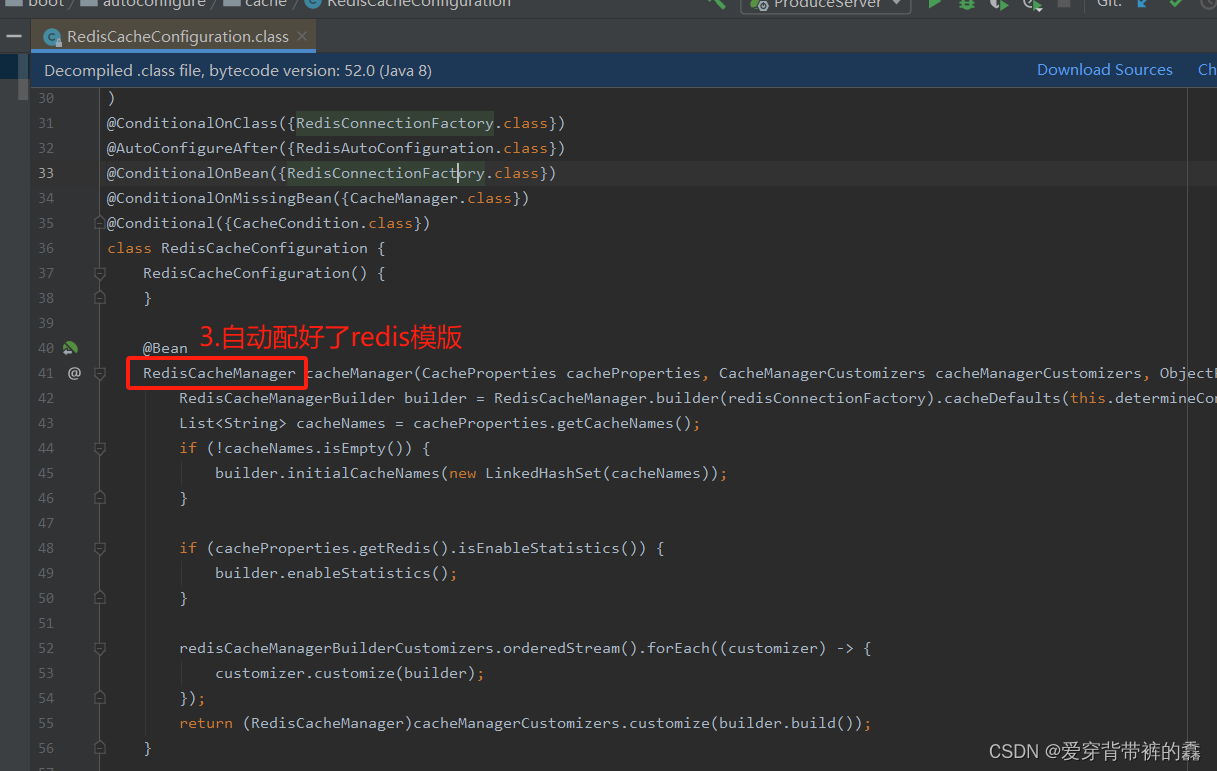
1. 定义全局二维数组 a 和 d，其中 a 用于存储原始矩阵，d 用于存储差分矩阵。

2. init_diff 函数初始化差分数组 d。对于差分数组中的每个元素 d[i][j]，它存储了原始矩阵 a 中元素 a[i][j] 相对于其左上角元素 a[i-1][j-1] 的差值的累计。这是通过计算 a[i][j]、a[i-1][j]、a[i][j-1] 和 a[i-1][j-1] 之间的差值来完成的。

3. update_diff 函数实现了差分数组的区间更新。它接收左上角坐标 (x1,y1) 和右下角坐标 (x2,y2)，以及更新值 c。该函数通过在差分数组的特定点上增加 c 以及在需要减少的点上减少 c 来更新区间。

4. 主函数 main 首先读取矩阵大小 n x m 和操作数量 q。

5. 读取初始球筐矩阵，并利用 init_diff 函数初始化差分数组。

6. 读取并执行 q 次操作更新，每次更新都调用 update_diff 函数。

7. 更新完成后，使用差分数组 d 通过累加前缀和来还原最终的球筐矩阵 a。

8. 最后，输出最终更新后的球筐矩阵。

这段代码使用了一种称为“差分”的技术，可以在 O(q + n * m) 的时间复杂度内完成所有更新和最终的输出，这对于大规模更新来说非常高效。在更新操作过程中，并不直接修改原始矩阵，而是通过差分矩阵间接记录每个区间增量的变化，然后在最后一步通过累加差分矩阵来重构原始矩阵。这种方法避免了对每个元素逐一更新带来的高时间复杂度。