1. 删除公共字符串
输入两个字符串,从第一字符串中删除第二个字符串中所有的字符。
例如,输入”They are students.”和”aeiou”,则删除之后的第一个字符串变成”Thy r stdnts.”
输入描述
每个测试输入包含2个字符串
输出描述
输出删除后的字符串
示例 1
输入
They are students.
aeiou
输出
Thy r stdnts.
思路1:
- 遍历第二个字符串
- 在第一个字符串中找到
跟第二个字符串相同的字符并逐一删除
int main() {
string one, two;
// cin遇到空格读取结束,所以用getline读取字符串里的空格
getline(cin, one);
getline(cin, two);
for (int i = 0; i < two.size(); i++) {
while (one.find(two[i]) != -1) // find失败返回值为-1
one.erase(one.find(two[i]), 1);
}
cout << one;
return 0;
}
思路2:
- 将第二个字符串的所有字符映射到哈希表
- 定义一个string
- 遍历第一个字符串
并在哈希表对应位置查找有无此字符
该位置为0说明第二个字符串无此字符
在新定义的string添加该字符即可
int main() {
string one, two;
getline(cin, one);
getline(cin, two);
int hashtable[256]={0}; // 哈希映射
for(size_t i = 0; i < two.length(); i++)
{
hashtable[two[i]]++; // 将第二个字符串中的字符映射到哈希表
}
string s;
for(size_t i = 0; i < one.length(); i++)
{
if(hashtable[one[i]] == 0)
{
s += one[i];
}
}
cout << s;
return 0;
}
2. 组队竞赛
牛牛举办了一次编程比赛,参加比赛的有3n个选手,每个选手都有一个水平值a_i.现在要将这些选手进行组队,一共组成n个队伍,即每个队伍3人.牛牛发现队伍的水平值等于该队伍队员中第二高水平值。
例如:
一个队伍三个队员的水平值分别是3,3,3.那么队伍的水平值是3
一个队伍三个队员的水平值分别是3,2,3.那么队伍的水平值是3
一个队伍三个队员的水平值分别是1,5,2.那么队伍的水平值是2
为了让比赛更有看点,牛牛想安排队伍使所有队伍的水平值总和最大。
如样例所示:
如果牛牛把6个队员划分到两个队伍
如果方案为:
team1:{1,2,5}, team2:{5,5,8}, 这时候水平值总和为7.
而如果方案为:
team1:{2,5,8}, team2:{1,5,5}, 这时候水平值总和为10.
没有比总和为10更大的方案,所以输出10.
输入描述
输入的第一行为一个正整数n(1 ≤ n ≤ 10^5)
第二行包括3n个整数a_i(1 ≤ a_i ≤ 10^9),表示每个参赛选手的水平值.
输出描述
输出一个整数表示所有队伍的水平值总和最大值.
示例 1
输入
2
5 2 8 5 1 5
输出
10
思路1:
用两大带一小的取法
可以保留次大的数据
从而提高队伍水平值
使水平值总和最大化
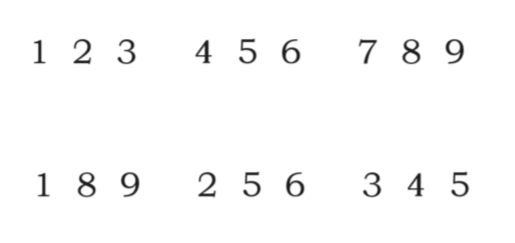
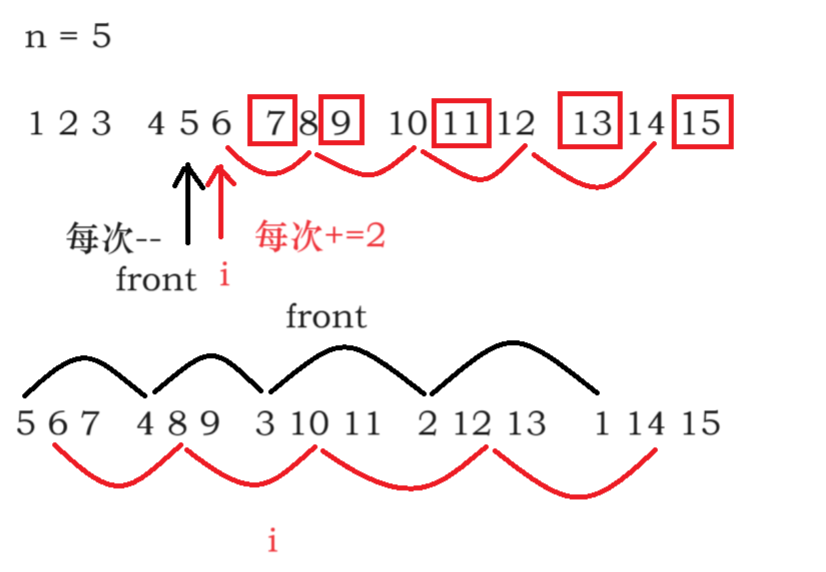
- 将3n个数据排序
- 从n+1个数隔1取1
int main() {
int n = 0;
cin >> n;
vector<int> v;
v.resize(3 * n);
// 输入3*n个元素放入vector
for (int i = 0; i < v.size(); i++)
{
cin >> v[i];
}
// 排序
sort(v.begin(), v.end());
// tail指向n的位置每次+=2,front指向n-1的位置每次--
vector<int> tmp;
long long max = 0;
for (int front = n-1, tail = n; tail < v.size(); tail += 2)
{
max += v[tail];
}
cout << max;
return 0;
}
3. 倒置字符串
将一句话的单词进行倒置,标点不倒置
比如 “I like beijing.”,经过处理后变为:“beijing. like I”。
字符串长度不超过100。
输入描述
输入一个仅包含小写字母、空格、‘.’ 的字符串,长度不超过100。
‘.’ 只出现在最后一个单词的末尾。
输出描述
依次输出倒置之后的字符串,以空格分割。
示例 1
输入
I like beijing.
输出
beijing. like I
思路1:
- 遍历字符串找到空格下标
- 通过找到的区间构建一个string插入vector
- 逆置输出vector
int main() {
string s;
getline(cin, s);
vector<string> v;
size_t sub = 0;
for (int i = 0; i < s.size(); i++)
{
// 找空格所在下标
while (s[sub] != ' ' && (s.begin() + sub) != s.end())
{
sub++;
}
string tmp(s, i, sub-i);
v.push_back(tmp);
i = sub;
sub++;
}
auto it = v.rbegin();
while (it != v.rend())
{
cout << *it << " ";
it++;
}
return 0;
}
思路2:
- 整体逆置
- 单词逆置

int main()
{
string s;
getline(cin, s);
// 整体逆置
reverse(s.begin(), s.end());
auto it = s.begin();
auto blank = s.begin();
while (it != s.end())
{
while (blank != s.end() && *blank != ' ')
{
blank++;
}
//局部单词逆置
reverse(it, blank);
if (blank != s.end())
blank++;
it = blank;
}
cout << s << endl;
return 0;
}
思路3:
- 只可意会不可言传
请自行画图理解
int main()
{
string s1, s2;
cin >> s1;
while (cin >> s2)
s1 = s2 + " " + s1;
cout << s1 << endl;
return 0;
}
4. 排序子序列
牛牛定义排序子序列为一个数组中一段连续的子序列,这段子序列是非递增或者非递减排序的。
牛牛有一个长度为 n 的整数数组 a,他现在需要把数组 a 分为若干段排序子序列,牛牛想知道最少可以把这个数组分为几段排序子序列。
输入描述
第一行输入一个正整数 n。
第二行输入 n 个正整数 a_i,表示数组的每个数。
1 <= n <= 10^5
1 <= a_i <= 10 ^ 9
输出描述
输出一个整数,可以将 a 最少划分为多少段排序子序列。
示例 1
输入
6
1 2 3 2 2 1
输出
2
说明
可以把划分为[1,2,3]和[2,2,1]两个排序子序列。
- 开始遍历数组,判断后一个数是否大于当前数
如果大于进入非递减序列
如果小于或等于进入非递增序列
int main() {
int n = 0;
cin >> n;
vector<int> v;
v.resize(n);
for (int i = 0; i < n; i++) {
cin >> v[i];
}
int count = 0;
for (int i = 0; i < v.size(); i++) {
if (i == v.size() - 1) // 当走到只剩最后一个元素的时候
{
count++;
break;
}
while (i + 1 != v.size() && v[i + 1] == v[i])
{
i++; // 刚开始遇到前后一样的元素直接++
// 因为不知道后面遇到的元素是非递增还是非递减
continue;
}
if (v[i + 1] > v[i])
{
while (i + 1 != v.size() && v[i + 1] >= v[i])
i++;
count++;
// 此时i指向非递减区间最后一个元素的下标
continue; // 需要跳出此次循环++到下一个非递增的第一个元素
}
if (v[i + 1] < v[i])
{
while (i + 1 != v.size() && v[i + 1] <= v[i])
i++;
count++;
}
}
cout << count;
return 0;
}