特征分解（Eigenvalue Decomposition）是将一个方阵分解为特征向量和特征值的过程。对于一个 n×n 的方阵A，其特征向量（Eigenvector）v 和特征值（Eigenvalue）
λ 满足以下关系：

这可以写成特征方程的形式：

其中，I是n×n 的单位矩阵，det(⋅) 表示矩阵的行列式。解特征方程得到的特征值λ是方阵A的特征值，而解特征方程得到的特征向量 v 对应于每个特征值。

特征分解的表达式为：

其中，V 是包含特征向量的矩阵，Λ 是对角矩阵，对角线上的元素是特征值。特征分解的应用非常广泛，例如在主成分分析（PCA）中，特征分解被用来找到数据的主成分。

假设我们有一个 2×2 的矩阵 A 如下：

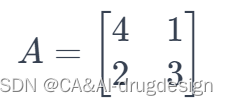
首先，我们需要解特征方程：

对于矩阵 A，特征方程为：

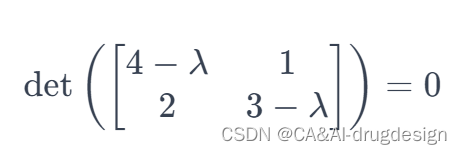
解这个方程可以得到特征值λ1=5 和λ2=2。