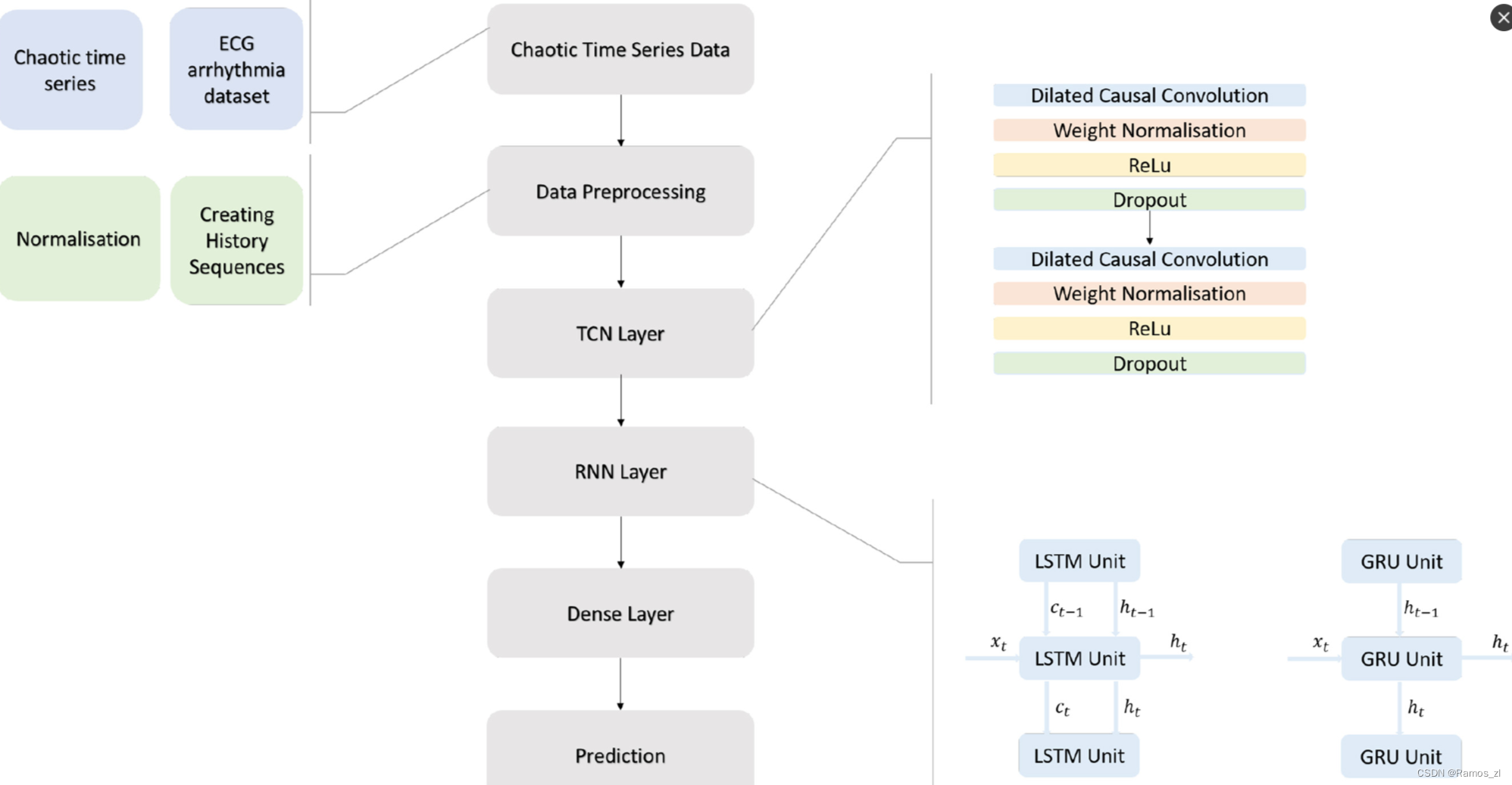
比赛地址
卡在第三题了,应该看看第4题kmp套模版的
一、最大频率元素计数
class Solution:
def maxFrequencyElements(self, nums: List[int]) -> int:
frequency = {} # 哈希表用于统计频率
max_freq = 0 # 存储最大频率
# 统计每个元素的频率
for num in nums:
if num in frequency:
frequency[num] += 1
else:
frequency[num] = 1
max_freq = max(max_freq, frequency[num])
# 计算具有最大频率的元素的总频率
total = 0
for freq in frequency.values():
if freq == max_freq:
total += freq
return total二、找出数组中的美丽下标 I
class Solution:
def beautifulIndices(self, s: str, a: str, b: str, k: int) -> List[int]:
# 找出所有子字符串a和b的出现位置
indices_a = [i for i in range(len(s) - len(a) + 1) if s[i:i + len(a)] == a]
indices_b = [i for i in range(len(s) - len(b) + 1) if s[i:i + len(b)] == b]
beautiful_indices = []
# 检查每个a的出现位置是否存在满足条件的b的出现位置
for i in indices_a:
for j in indices_b:
if abs(j - i) <= k:
beautiful_indices.append(i)
break
return beautiful_indices三、 价值和小于等于 K 的最大数字
二分查找:
findMaximumNumber函数使用二分查找法来查找符合条件的最大num。它初始化左边界left为 0,右边界right为(k + 1) << (x - 1)。这个右边界是一个估计值,确保num的上界足够高。二分查找在满足条件left + 1 < right的情况下迭代,通过比较countDigitOne(mid)和k来调整left和right。递归函数
dfs:这是一个深度优先搜索函数,用于计算在1到num的范围内,满足特定条件的设置位的总数。它采用记忆化搜索来优化性能,减少重复计算。参数i是当前正在处理的二进制位的位置,cnt1是当前累计的设置位数量,isLimit表示是否受到num的限制。记忆化搜索:在
dfs函数中,如果不受num的限制且已经计算过该状态,则直接返回存储的结果(memo[i][cnt1])。这样避免了重复计算,提高了效率。计算设置位的数量:
dfs函数枚举在当前位置i可能的数字(0 或 1),并递归计算接下来的位。如果当前位是设置位且满足(i + 1) % x == 0的条件,则cnt1增加。这样累加所有满足条件的设置位数量。寻找最大
num:通过二分查找和dfs函数的结合,最终确定出使得从 1 到num的所有整数的价值和小于等于k的最大num。
class Solution {
private int x;
private long num;
private long memo[][];
// 主方法:找到最大的num,使得从1到num的所有整数的价值和小于等于k
public long findMaximumNumber(long k, int x) {
this.x = x;
// 使用二分查找法来找到满足条件的最大num
// 初始右边界是一个估计值,足够大以涵盖可能的解,左闭右开区间,寻找右侧边界
long left = 0;
long right = k << x;
while (left < right) {
long mid = left + (right - left) / 2;
if (countDigitOne(mid) < k) {
left = mid+1;
} else if(countDigitOne(mid) == k){
left = mid+1;
}else{
right = mid;
}
}
return left-1;
}
// 计算从1到num的所有整数的价值和
public long countDigitOne(long num) {
this.num = num; // 将类变量num设置为当前处理的数字
int m = 64 - Long.numberOfLeadingZeros(num); // 计算num的二进制表示的长度
memo = new long[m][m + 1]; // 初始化记忆化数组,用于存储中间结果
for (long[] row : memo) {
Arrays.fill(row, -1); // 将记忆化数组的每个元素初始化为-1,表示未计算
}
return dfs(m - 1, 0, true); // 调用深度优先搜索函数计算设置位的数量
}
// 深度优先搜索计算设置位的数量
// i 是当前处理的位的索引,cnt1 是当前累计的设置位数量,isLimit 表示是否受到num的限制
long dfs(int i, int cnt1, boolean isLimit) {
if (i < 0) return cnt1; // 如果索引小于0,返回累计的设置位数量
if (!isLimit && memo[i][cnt1] != -1) return memo[i][cnt1]; // 记忆化搜索,避免重复计算
int up = isLimit ? (int) (num >> i & 1) : 1; // 受限的话,上限取决于num的第i位,不受限的话上限为1
long res = 0;
for (int d = 0; d <= up; d++) { // 枚举要填入的数字d
res += dfs(i - 1, cnt1 + (d == 1 && (i + 1) % x == 0 ? 1 : 0), isLimit && d == up);
}
if (!isLimit) memo[i][cnt1] = res; // 更新记忆化存储
return res;
}
}如果k=10000100 (8位数),x=6,对于2<<6 即100000(6位数) 第6为确定为1的画后面有2^(6-1)个组合方案。

四、找出数组中的美丽下标 II
普通的算法会超时需要用到二分法和KMP算法
- 用 KMP 求出 aaa 在 sss 中的所有出现位置,记作 posA 。
- 用 KMP 求出 bbb 在 sss 中的所有出现位置,记作 posB。
- 遍历 posA 中的下标 ,在 posB 中二分查找离 i 最近的 j。如果 ∣i−j∣≤k ,则把 i 加入答案。
class Solution:
def beautifulIndices(self, s: str, a: str, b: str, k: int) -> List[int]:
# 使用KMP算法找出字符串a和b在s中所有的出现位置
pos_a = self.kmp(s, a)
pos_b = self.kmp(s, b)
ans = []
# 遍历a在s中的每个出现位置
for i in pos_a:
# 使用二分查找在b的出现位置中找到大于等于i的最小索引
bi = bisect_left(pos_b, i)
# 检查找到的b的位置是否满足与a的位置距离不超过k的条件
if (bi < len(pos_b) and pos_b[bi] - i <= k) or \
(bi > 0 and i - pos_b[bi - 1] <= k):
ans.append(i) # 如果满足条件,将a的位置添加到结果列表中
return ans
def kmp(self, text: str, pattern: str) -> List[int]:
# 初始化部分匹配表
m = len(pattern)
pi = [0] * m
# 构建部分匹配表
c = 0
for i in range(1, m):
while c and pattern[c] != pattern[i]:
c = pi[c - 1]
if pattern[c] == pattern[i]:
c += 1
pi[i] = c
# 在文本中搜索模式
res = []
c = 0
for i, v in enumerate(text):
while c and pattern[c] != v:
c = pi[c - 1]
if pattern[c] == v:
c += 1
if c == m:
res.append(i - m + 1) # 找到一个匹配,记录其开始位置
c = pi[c - 1] # 继续搜索下一个可能的匹配
return res
- bi < len(pos_b):这个条件确保 bi 是 pos_b 中的有效索引。由于 bisect_left 返回的 bi 是 pos_b 中第一个大于或等于 i 的元素的索引,可能会出现 bi 等于 pos_b 的长度的情况,这意味着所有 b 的出现位置都在 i 之前。在这种情况下,尝试访问 pos_b[bi] 会导致数组越界。因此,需要检查 bi < len(pos_b) 来确保访问是安全的。
- bi > 0:这个条件用于检查 pos_b[bi - 1] 是否是有效访问。当 bi 为 0 时,bi - 1 会变成 -1,这在 Python 中是有效的倒数第一个元素的索引,但在某些编程语言中可能会导致错误。在这里,bi > 0 确保我们不会尝试访问列表的负索引,这对于理解代码逻辑和避免潜在错误是重要的。
对应的java写法
class Solution {
public List<Integer> beautifulIndices(String s, String a, String b, int k) {
char[] text = s.toCharArray();
List<Integer> posA = kmp(text, a.toCharArray());
List<Integer> posB = kmp(text, b.toCharArray());
List<Integer> ans = new ArrayList<>();
for (int i : posA) {
int bi = lowerBound(posB, i);
if (bi < posB.size() && posB.get(bi) - i <= k ||
bi > 0 && i - posB.get(bi - 1) <= k) {
ans.add(i);
}
}
return ans;
}
private List<Integer> kmp(char[] text, char[] pattern) {
int m = pattern.length;
int[] pi = new int[m];
int c = 0;
for (int i = 1; i < m; i++) {
char v = pattern[i];
while (c > 0 && pattern[c] != v) {
c = pi[c - 1];
}
if (pattern[c] == v) {
c++;
}
pi[i] = c;
}
List<Integer> res = new ArrayList<>();
c = 0;
for (int i = 0; i < text.length; i++) {
char v = text[i];
while (c > 0 && pattern[c] != v) {
c = pi[c - 1];
}
if (pattern[c] == v) {
c++;
}
if (c == m) {
res.add(i - m + 1);
c = pi[c - 1];
}
}
return res;
}
private int lowerBound(List<Integer> nums, int target) {
int left = 0, right = nums.size(); // 开区间 (left, right)
while (left < right) { // 区间不为空
// 循环不变量:
// nums[left] < target
// nums[right] >= target
int mid = (left + right) >>> 1;
//不要写成 int mid = left + (right - left) >>> 1; 会超时
if (nums.get(mid) < target) {
left = mid+1; // 范围缩小到 [mid+1, right)
} else {
right = mid; // 范围缩小到 (left, mid)
}
}
return right;
}
}
数位 DP相关问题
2719. 统计整数数目 入门题
788. 旋转数字(题解)
902. 最大为 N 的数字组合(题解)1990
233. 数字 1 的个数(题解)
面试题 17.06. 2 出现的次数(题解)
600. 不含连续 1 的非负整数(题解)
2376. 统计特殊整数(题解)2120
1012. 至少有 1 位重复的数字(题解)2230
357. 统计各位数字都不同的数字个数
2999. 统计强大整数的数目
2827. 范围中美丽整数的数目 2324
2801. 统计范围内的步进数字数目 2367
1397. 找到所有好字符串 2667
1742. 盒子中小球的最大数量 *非暴力做法