2章-Pigeonhole Principle鸽子洞原理

A Theorem of Ramsey

• 考虑一个有趣的事实：任意6个人，其中至少有3个人互相不认识，或者互相认识
• 可以将它用图论的语言进行描述：给一个K₆（6个节点的完全图）的边涂上红色或者蓝色中的一种颜色，则存在一个红色或者蓝色三角形。这个结论记为：K₆->K₃,K₃
• 证明：考虑图K₆的任意一种着色，任取一个点x，不妨假设连接它的边中颜色较多的为红色，设所有红边对应的点为R_x，如果R_x中存在一条红边，则它们和x构成一个红色三角形.否则它们之间都是蓝色边，由于点数至少为3，因此至少有一个蓝色三角形.证毕

推广

If m≥2 and n ≥2 are integers, then there is a positive integer p such that Kp → Km,Kn.
a. If Kp → Km,Kn, for any integer q ≥ p, Kq → Km,Kn.
b. The Ramsey number r (m, n) is the smallest integer p such that Kp → Km,Kn. e.g., r(3,3) = 6.

3章-Permutations and combinations排列与组合

3-1Addition and multiplication principle加法和乘法原理

A有n种B有m种，既A又B有nm种，A或B有n+m种

3-2Permutations of sets集合置换

• r-排列数 P(n,r) =n!/(n-r)!，也就是n种前r大的数相乘
• 对象排一排叫linear permutations，排一圈叫circular permutations，The number of circular r-permutations of a set of n elements is given by P(n,r)/r

3-3Combinations of sets集合组合

• r-combination C(n,r) =P(n,r)/r! =n!/((n-r)!r!), 也可以写成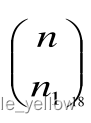其中n1就是r

• C(n,r) = C(n, n−r)

3-4Permutations of multi-sets多重集置换

• 无穷多重集，有k类的r-置换数为k^r
• 有穷多重集，有k类的n-置换数为n!/(n₁!n₂!..n_k!)，n=2时为C(n,n₁)
• 多重集棋盘放rook问题：n*n棋盘rook不能互攻，有k个颜色，每个颜色分别有rook n₁ ~ n_k个，放rook数为 (n!)² /(n₁!n₂!..n_k!)。思路为先选位置，再选有穷多重集有k类的n-置换。

3-5Combinations of multi-sets多重集组合

• 有穷多重集，穷举法
• 无穷多重集，k类的r-组合为
  这也和方程的解有关：x1 + x2 + … + xk = r的non-negative integer solution非负整数解
  证明：有k-1个隔板用来分类
  

4章-Generating Permutations and Combinations生成置换和组合

4-1Generating permutations生成置换

4-2Inversions in Permutations排列中的反转

4-3Generating combinations生成组合

4-4Generating r-combinations生成r-组合

5章-The Binomial Coefficients二项式系数

5-1Pascal’s formula

5-2The binomial theorem二项式定理

5-3Identities恒等式

5-4Unimodality of binomial coefficients二项式系数的唯一性

5-5The multinomial theorem多项式定理

5-6Newton’s binomial theorem牛顿二项式定理

n->a，正整数->实数

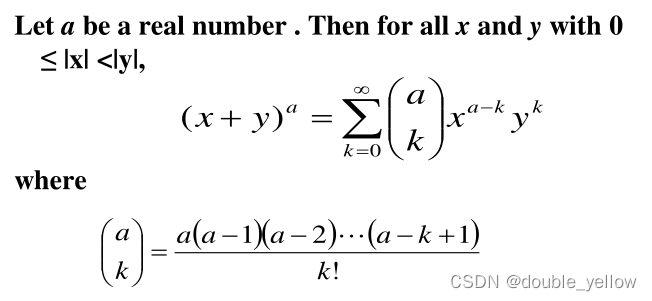
当a=-n

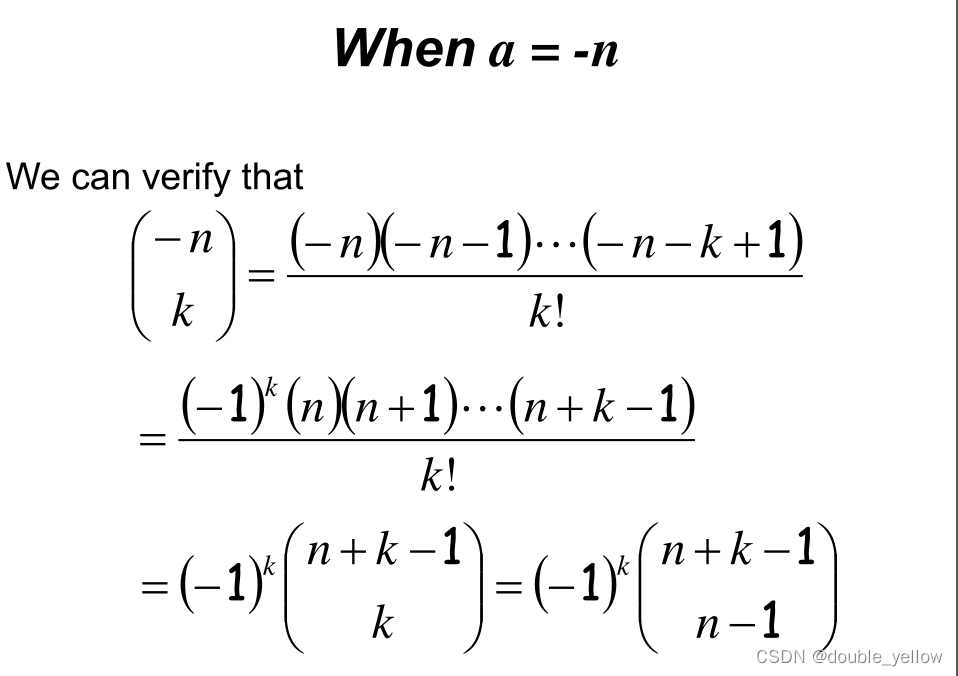
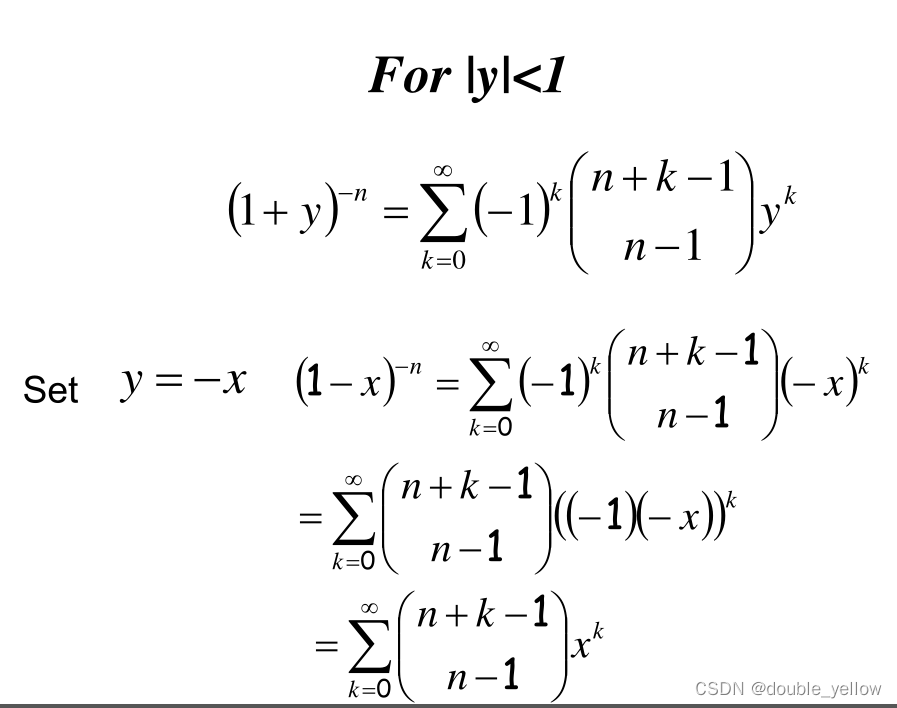
6章-IEP and Applications容斥原理

6-1The inclusion-exclusion principle容斥原理

6-2Combinations with repetition组合与重复

6-3Derangements

6-4Permutations with forbidden positions与禁止位置的排列

14章-Polya counting波利亚计数

14-1Permutation and symmetry groups 置换群和对称群

1.等价着色和不等价着色（equivalent/inequivalent）：对于四面体和正方形，如果允许自由移动
2.置换（Permutation）：f: X -> X
置换的组合，下面是先后g

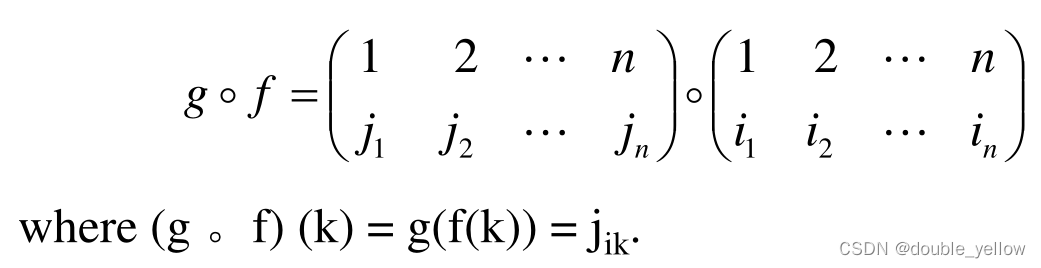
如果置换的set有n个元素，那么有n!种置换，这个集合叫作S_n是一个set（set应该是集合的意思）
3.置换群(Permutation group)：

• 若f, g在群里，那么f○g也在群里
• l( The identity permutation，恒等置换)在群里
• 如果f在群里，那么 f^-1在群里

4.对称（Symmetry）：让几何图形保持原样的置换

• 对称群包括n元循环群(a cyclic group of order n，ρ_n^k)(rotations acting)，和对称操作的置换群(reflections acting，r_k）
  点/边置换群就是点/边的排列
• G_C = {ρ_n⁰=l, ρ_n, ρ_n²,…, ρ_n^n-1, r₁, r₂, …, r_n} of 2n permutations of {1, 2, …, n} is an instance of a dihedral group of order 2n ( ｛1，2，…，n｝的2n个排列G_C是2n阶二面体群的一个例子 )

5.Coloring，f*c问题

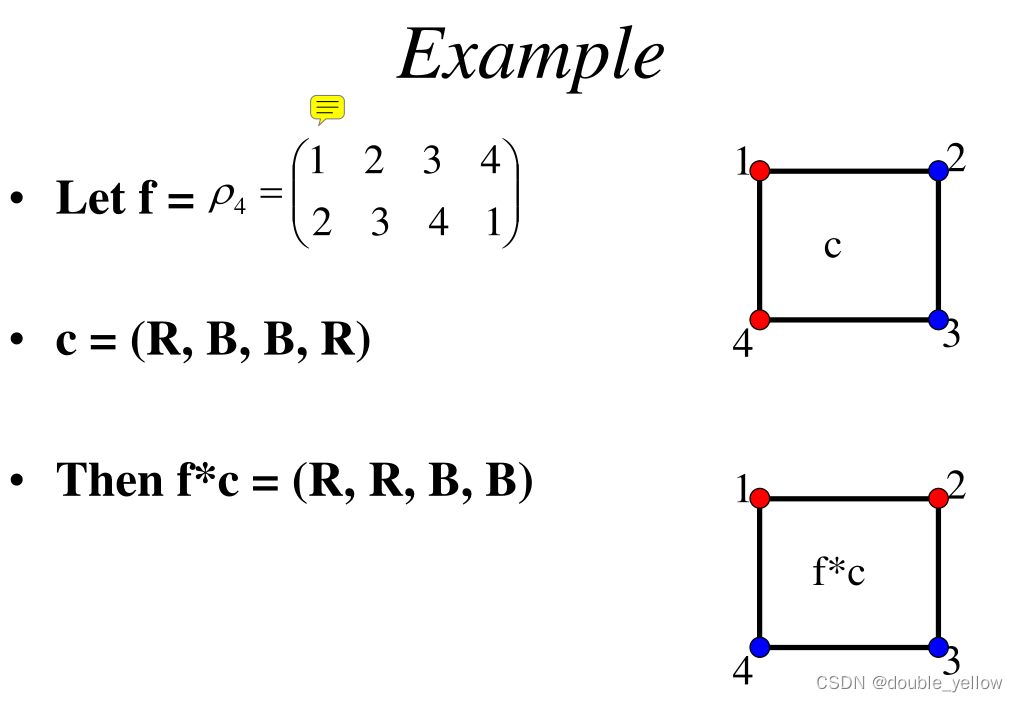
所以1->2的置换是：1去到2的位置（而不是2填上1的位置）

• 置换f有两行，可以理解为动作；实际颜色c只有一行，意思是结果，这两者不一样

6.稳定剂/稳定核（Stabilizer ）：

• 颜色等价：c1经过f能变为c2，则等价；
• G( c ) = {f: f in G, f*c = c}是G对c的Stabilizer ，让c继续保持原样的置换集合，是一个置换群
• 同理有C(f) = {c: c in C, f*c = c}
• 其中G和C分别是X的置换群和着色集合，X = {1, 2, …, n}

7.非等价着色数是什么：N（G,C）
和与c等价的着色数

• 等价着色数： 等价着色是指考虑到对称性质后，两种着色方案被认为是相同的。换句话说，如果两个着色方案可以通过图的自同构来映射，那么它们是等价的。等价着色数就是考虑了这些自同构映射的着色方案的数量。这个数目更关注结构相似而颜色不同的情况。

• 非等价着色数： 非等价着色数则是不考虑图的自同构，只考虑颜色方案不同的情况下的着色数。这个数目更关注颜色方案的差异，而不在乎通过自同构可以将它们映射到一起的情况。

• 举个简单的例子，考虑一个三角形图。如果我们着色这个图的三个顶点，如果两种着色方案可以通过旋转三角形来相互映射，那么它们是等价的。如果我们只关心颜色不同的情况，而不考虑这种旋转，那么就是在考虑非等价的情况。

• 在实际的问题中，通常我们更关心等价着色数，因为这更能反映图的结构性质。非等价着色数则在某些特定的问题或者特定的应用场景中可能更为重要。

8.为什么做题的置换群大小只包含循环群或翻转群：因为要让图形保持原形的置换为对称群

14-2Burnside theorem 伯恩赛德定理

14-3Polya counting formula 波利亚计数公式