题目

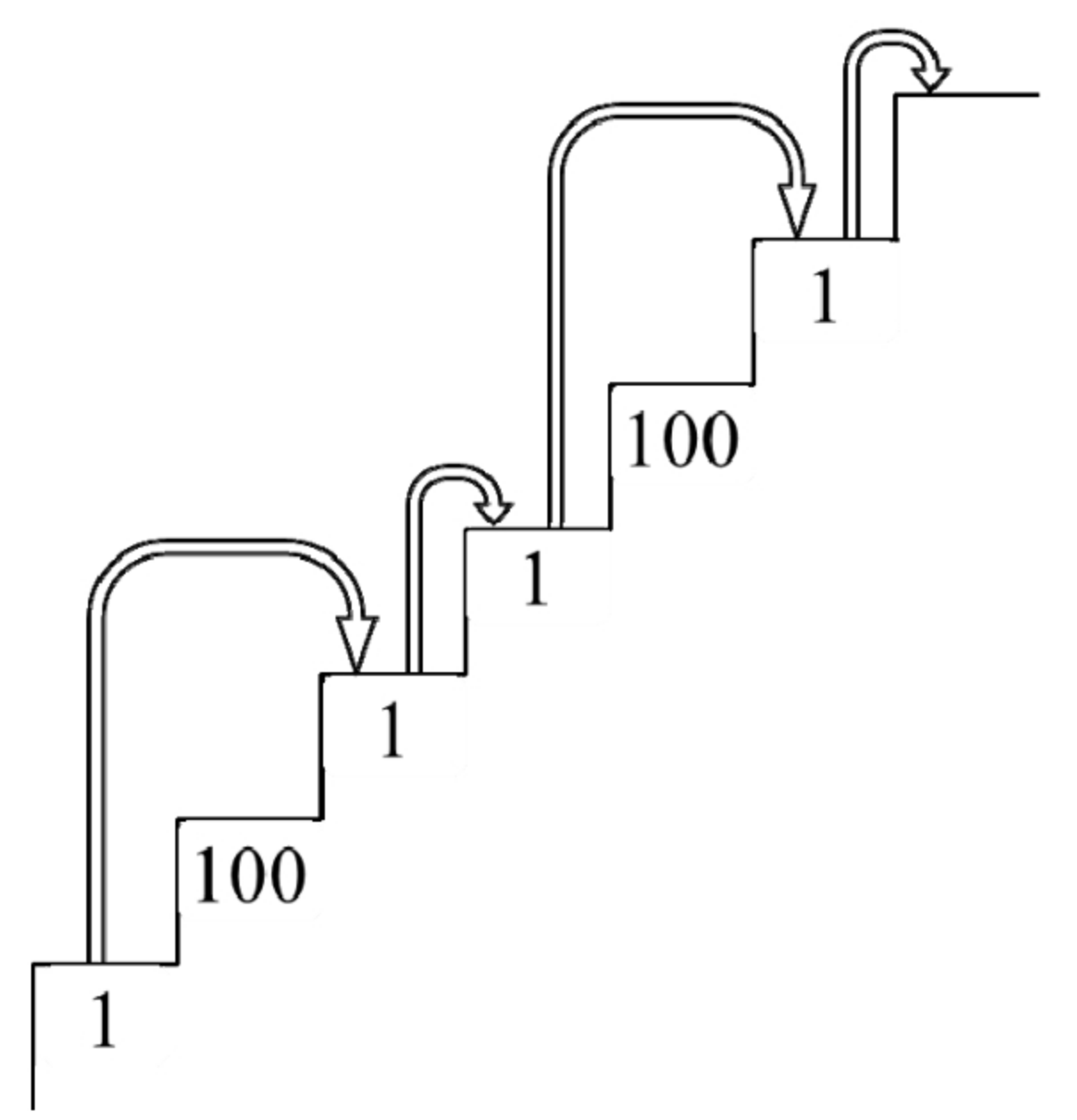
一个数组cost的所有数字都是正数，它的第i个数字表示在一个楼梯的第i级台阶往上爬的成本，在支付了成本cost[i]之后可以从第i级台阶往上爬1级或2级。假设台阶至少有2级，既可以从第0级台阶出发，也可以从第1级台阶出发，请计算爬上该楼梯的最少成本。例如，输入数组[1，100，1，1，100，1]，则爬上该楼梯的最少成本是4，分别经过下标为0、2、3、5的这4级台阶，如图14.1所示（注意：最上一级台阶是没有成本的）。

分析

分析1

爬上一个有多级台阶的楼梯自然需要若干步。按照题目的要求，每次爬的时候既可以往上爬1级台阶，也可以爬2级台阶，也就是每一步都有两个选择。这看起来像是与回溯法有关的问题。但这个问题不是要找出有多少种方法可以爬上楼梯，而是计算爬上楼梯的最少成本，即计算问题的最优解，因此解决这个问题更适合运用动态规划。

分析2：确定状态转移方程

这个问题要求计算爬上楼梯的最少成本，可以用函数f（i）表示从楼梯的第i级台阶再往上爬的最少成本。如果一个楼梯有n级台阶（台阶从0开始计数，从第0级一直到第n-1级），由于一次可以爬1级或2级台阶，因此最终可以从第n-2级台阶或第n-1级台阶爬到楼梯的顶部，即f（n-1）和f（n-2）的最小值就是这个问题的最优解。
应用动态规划的第1步是找出状态转移方程，即用一个等式表示其中某一步的最优解和前面若干步的最优解的关系。根据题目的要求，可以一次爬1级或2级台阶，既可以从第i-1级台阶爬上第i级台阶，也可以从第i-2级台阶爬上第i级台阶，因此，从第i级台阶往上爬的最少成本应该是从第i-1级台阶往上爬的最少成本和从第i-2级台阶往上爬的最少成本的较小值再加上爬第i级台阶的成本。这个关系可以用状态转移方程表示为f（i）=min（f（i-1），f（i-2））+cost[i]。

分析3

上述状态转移方程有一个隐含的条件，即i大于或等于2。如果i小于2怎么办？如果i等于0，则可以直接从第0级台阶往上爬，f（0）等于cost[0]。如果i等于1，题目中提到可以从第1级台阶出发往上爬，因此f（1）等于cost[1]。

解

public class Test {
    public static void main(String[] args) {
        int[] cost = {1, 100, 1, 1, 100, 1};
        int result = minCostClimbingStairs(cost);
        System.out.println(result);

    }

    public static int minCostClimbingStairs(int[] cost) {
        int len = cost.length;
        return Math.min(helper(cost, len - 2), helper(cost, len - 1));
    }

    private static int helper(int[] cost, int i) {
        if (i < 2) {
            return cost[i];
        }

        return Math.min(helper(cost, i - 2), helper(cost, i - 1)) + cost[i];
    }
}

分析4

上述代码看起来很简捷，但时间效率非常糟糕。时间效率是面试官非常关心的问题，如果应聘者的解法的时间效率糟糕则很难通过面试。根据前面的递归代码，为了求得f（i）需要先求得f（i-1）和f（i-2）。如果将求解过程用一个树形结构表示（如图14.2中求解f（9）的过程），就能发现在求解过程中有很多重复的节点。例如，求解f（9）需要求解f（8）和f（7），而求解f（8）和f（7）都需要求解f（6），这就意味着在求解f（9）的过程中有重复计算。
求解f（i）这个问题的解，依赖于求解f（i-1）和f（i-2）这两个子问题的解，由于求解f（i-1）和f（i-2）这两个子问题有重叠的部分，如果只是简单地将状态转移方程转换成递归的代码就会带来严重的效率问题，因为重复计算是呈指数级增长的。
为了避免重复计算带来的问题，一个常用的解决办法是将已经求解过的问题的结果保存下来。在每次求解一个问题之前，应先检查该问题的求解结果是否已经存在。如果问题的求解结果已经存在，则不再重复计算，只需要从缓存中读取之前求解的结果。

解

public class Test {
    public static void main(String[] args) {
        int[] cost = {1, 100, 1, 1, 100, 1};
        int result = minCostClimbingStairs(cost);
        System.out.println(result);

    }

    public static int minCostClimbingStairs(int[] cost) {
        int len = cost.length;
        int[] dp = new int[len];
        helper(cost, len - 1, dp);
        return Math.min(dp[len - 2], dp[len - 1]);
    }

    private static void helper(int[] cost, int i, int[] dp) {
        if (i < 2) {
            dp[i] = cost[i];
        }
        else if (dp[i] == 0) {
            helper(cost, i - 2, dp);
            helper(cost, i - 1, dp);
            dp[i] = Math.min(dp[i - 2], dp[i - 1]) + cost[i];
        }
    }
}

分析5：空间复杂度为O（n）的迭代代码

也可以自下而上地解决这个过程，也就是从子问题入手，根据两个子问题f（i-1）和f（i-2）的解求出f（i）的结果。

解

public class Test {
    public static void main(String[] args) {
        int[] cost = {1, 100, 1, 1, 100, 1};
        int result = minCostClimbingStairs(cost);
        System.out.println(result);

    }

    public static int minCostClimbingStairs(int[] cost) {
        int len = cost.length;
        int[] dp = new int[len];
        dp[0] = cost[0];
        dp[1] = cost[1];

        for (int i = 2; i < len; i++) {
            dp[i] = Math.min(dp[i - 2], dp[i - 1]) + cost[i];
        }

        return Math.min(dp[len - 2], dp[len - 1]);
    }
}

分析6：空间复杂度为O（1）的迭代代码

上述迭代代码还能做进一步的优化。前面用一个长度为n的数组将所有f（i）的结果都保存下来。求解f（i）时只需要f（i-1）和f（i-2）的结果，从f（0）到f（i-3）的结果其实对求解f（i）并没有任何作用。也就是说，在求每个f（i）的时候，需要保存之前的f（i-1）和f（i-2）的结果，因此只要一个长度为2的数组即可。

解

public class Test {
    public static void main(String[] args) {
        int[] cost = {1, 100, 1, 1, 100, 1};
        int result = minCostClimbingStairs(cost);
        System.out.println(result);

    }

    public static int minCostClimbingStairs(int[] cost) {
        int[] dp = new int[] {cost[0], cost[1]};
        for (int i = 2; i < cost.length; i++) {
            dp[i % 2] = Math.min(dp[0], dp[1]) + cost[i];
        }

        return Math.min(dp[0], dp[1]);
    }
}