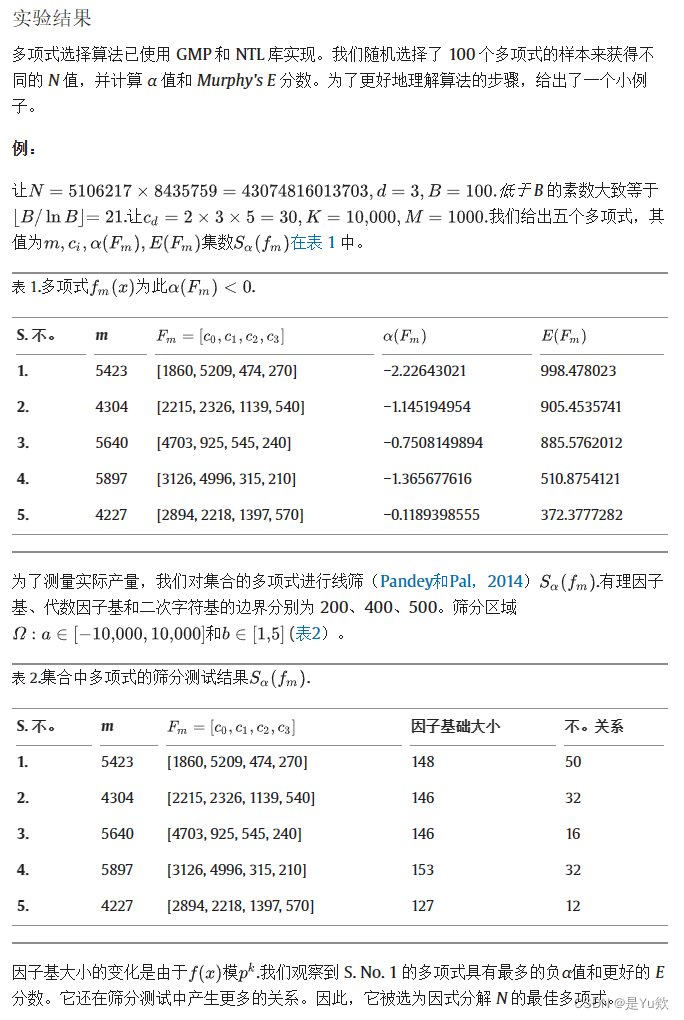
文章目录
- 前言
- 一、ComputeFogFactor 来计算雾效混合因子
- 二、UNITY_Z_0_FAR_FROM_CLIPSPACE 来统一计算不同平台下的Z值
- 1、DirectX平台
- 2、GL平台下(在Unity.2022.LTS下,该功能没有完善)
- 3、Opengl下
前言
在之前的文章中,我们实现了URP下的雾效。
- Unity中URP下的添加雾效支持
我们在这篇文章中,看一下Unity在URP下,计算雾效因子时是怎么统一Z值的。
一、ComputeFogFactor 来计算雾效混合因子
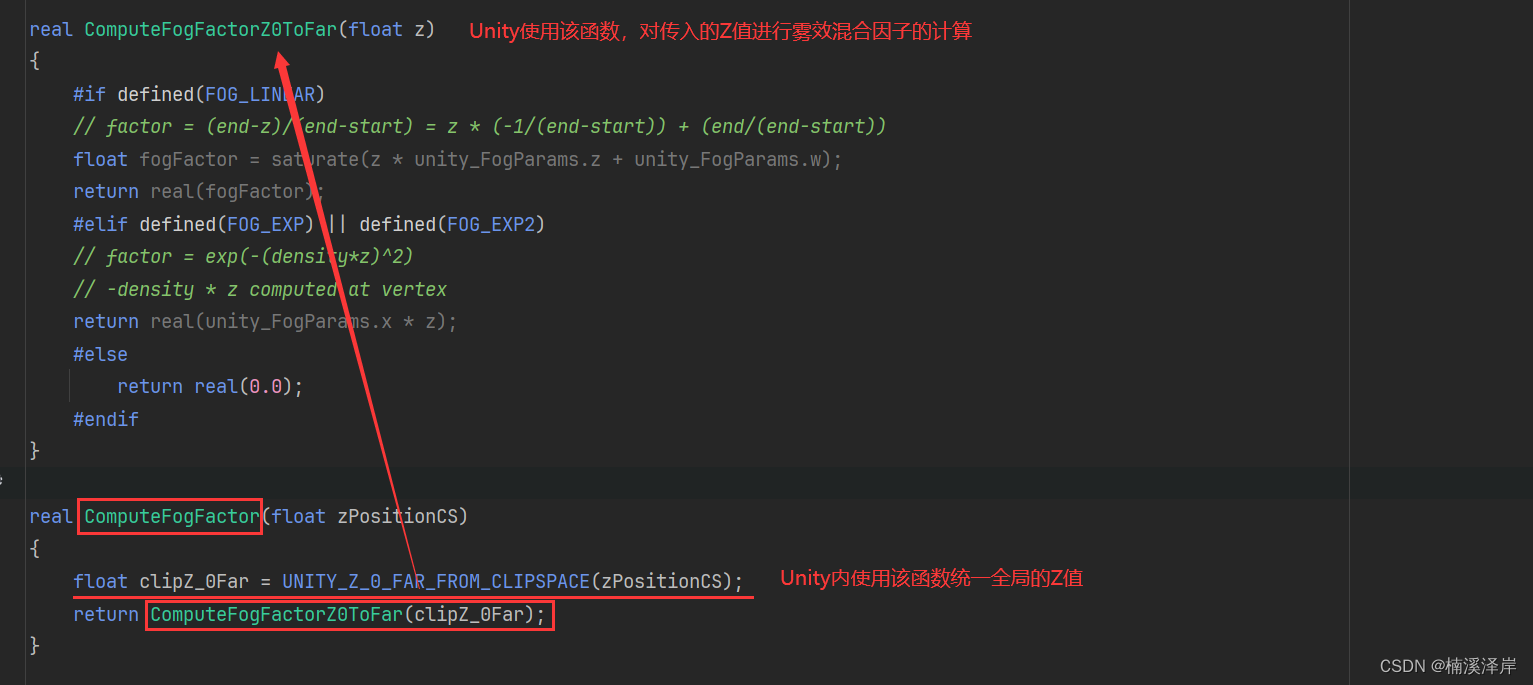
二、UNITY_Z_0_FAR_FROM_CLIPSPACE 来统一计算不同平台下的Z值
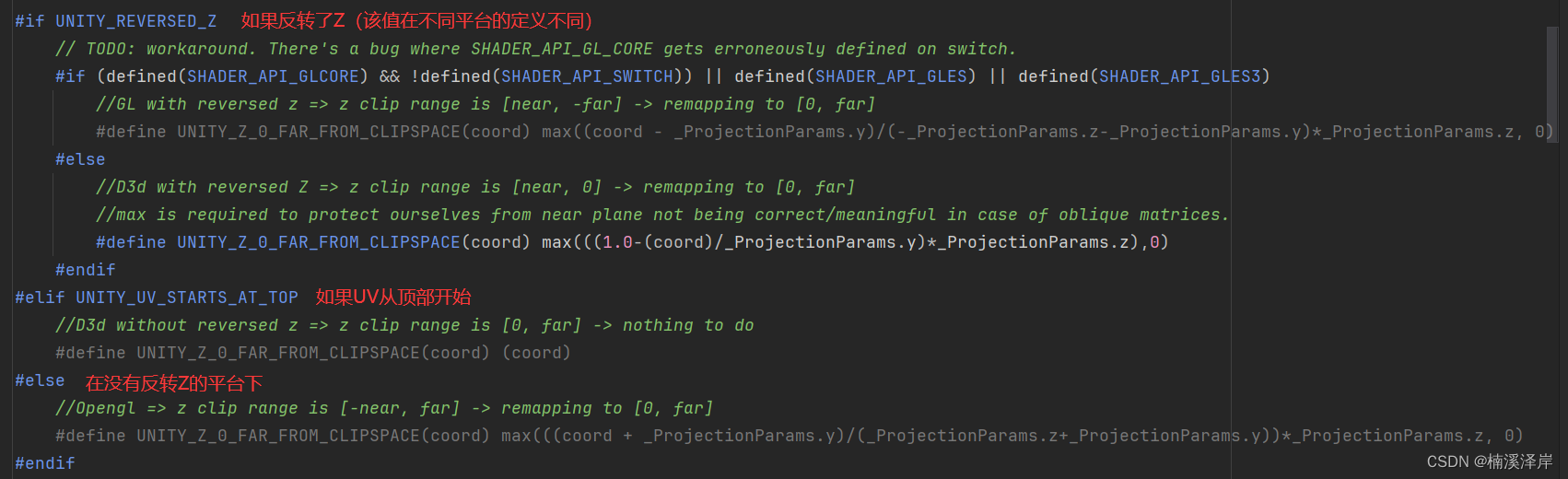
- UNITY_REVERSED_Z(DX类平台都为1,其他平台都为0)
- UNITY_UV_STARTS_AT_TOP(DX类平台都为1,其他平台都为0)
(这个的作用应该是防止出现什么奇怪的平台时,对传入的Z值不做处理)
1、DirectX平台
- 我们看一下反转过Z值的类DirectX平台,在处理雾效因子时,Z值是怎么处理的。
- [near, 0] -> remapping to [0, far]
//D3d with reversed Z => z clip range is [near, 0] -> remapping to [0, far]
//max is required to protect ourselves from near plane not being correct/meaningful in case of oblique matrices.
#define UNITY_Z_0_FAR_FROM_CLIPSPACE(coord) max(((1.0-(coord)/_ProjectionParams.y)*_ProjectionParams.z),0)
n ≤ z ≤ 0 n \leq z \leq0 n≤z≤0
n − n ≤ z − n ≤ 0 − n n - n \leq z - n\leq0 - n n−n≤z−n≤0−n
0 ≤ z − n ≤ − n 0 \leq z - n\leq- n 0≤z−n≤−n
0 ≤ ( z − n ) 1 − n ≤ − n 1 − n 0 \leq (z - n)\frac{1}{-n}\leq- n\frac{1}{-n} 0≤(z−n)−n1≤−n−n1
0 ≤ z − n − n ≤ 1 0 \leq \frac{z - n}{-n}\leq1 0≤−nz−n≤1
0 ≤ z − n − n f ≤ f 0 \leq \frac{z - n}{-n}f\leq f 0≤−nz−nf≤f
0 ≤ n − z n f ≤ f 0 \leq \frac{n - z}{n}f\leq f 0≤nn−zf≤f
0 ≤ ( n n − x n ) f ≤ f 0 \leq (\frac{n}{n}-\frac{x}{n})f\leq f 0≤(nn−nx)f≤f
0 ≤ ( 1 − x n ) f ≤ f 0 \leq (1-\frac{x}{n})f\leq f 0≤(1−nx)f≤f
- 最后得出的公式是和我们Unity中使用的公式是一致的
0 ≤ ( 1 − x n ) f ≤ f 0 \leq (1-\frac{x}{n})f\leq f 0≤(1−nx)f≤f
max(((1.0-(coord)/_ProjectionParams.y)*_ProjectionParams.z),0)
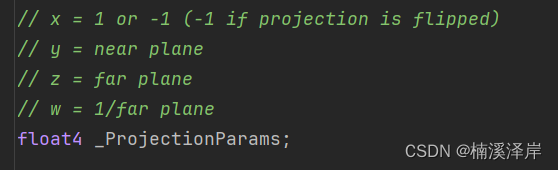
- _ProjectionParams在Unity中的定义
2、GL平台下(在Unity.2022.LTS下,该功能没有完善)
- 在GL平台下,我们也需要对Z值进行重映射
- [near, -far] -> remapping to [0, far]
//GL with reversed z => z clip range is [near, -far] -> remapping to [0, far]
#define UNITY_Z_0_FAR_FROM_CLIPSPACE(coord) max((coord - _ProjectionParams.y)/(-_ProjectionParams.z-_ProjectionParams.y)*_ProjectionParams.z, 0)
n ≤ z ≤ − f n \leq z \leq-f n≤z≤−f
n − n ≤ z − n ≤ − f − n n -n\leq z -n \leq-f - n n−n≤z−n≤−f−n
0 ≤ z − n ≤ − f − n 0\leq z -n \leq-f - n 0≤z−n≤−f−n
0 ≤ ( z − n ) 1 − f − n ≤ − ( f + n ) 1 − f − n 0\leq (z -n) \frac{1}{-f-n}\leq-(f + n)\frac{1}{-f-n} 0≤(z−n)−f−n1≤−(f+n)−f−n1
0 ≤ z − n − f − n ≤ 1 0\leq \frac{z-n}{-f-n}\leq1 0≤−f−nz−n≤1
0 ≤ z − n − f − n f ≤ f 0\leq \frac{z-n}{-f-n}f\leq f 0≤−f−nz−nf≤f
- 最后得出的公式是和我们Unity中使用的公式是一致的
0 ≤ z − n − f − n f ≤ f 0\leq \frac{z-n}{-f-n}f\leq f 0≤−f−nz−nf≤f
max((coord - _ProjectionParams.y)/(-_ProjectionParams.z-_ProjectionParams.y)*_ProjectionParams.z, 0)
3、Opengl下
- 在OpenGL平台下,我们
- [-near, far] -> remapping to [0, far]
//Opengl => z clip range is [-near, far] -> remapping to [0, far]
#define UNITY_Z_0_FAR_FROM_CLIPSPACE(coord) max(((coord + _ProjectionParams.y)/(_ProjectionParams.z+_ProjectionParams.y))*_ProjectionParams.z, 0)
− n ≤ z ≤ f -n \leq z \leq f −n≤z≤f
− n + n ≤ z + n ≤ f + n -n +n \leq z+n \leq f+n −n+n≤z+n≤f+n
0 ≤ z + n ≤ f + n 0\leq z+n \leq f+n 0≤z+n≤f+n
0 ≤ z + n 1 f + n ≤ ( f + n ) 1 f + n 0\leq z+n\frac{1}{f+n}\leq (f+n)\frac{1}{f+n} 0≤z+nf+n1≤(f+n)f+n1
0 ≤ ( z + n ) 1 f + n ≤ 1 0\leq (z+n)\frac{1}{f+n}\leq 1 0≤(z+n)f+n1≤1
0 ≤ ( z + n ) 1 f + n f ≤ f 0\leq (z+n)\frac{1}{f+n}f\leq f 0≤(z+n)f+n1f≤f
- 最后得出的公式是和我们Unity中使用的公式是一致的
0 ≤ ( z + n ) 1 f + n f ≤ f 0\leq (z+n)\frac{1}{f+n}f\leq f 0≤(z+n)f+n1f≤f
max(((coord + _ProjectionParams.y)/(_ProjectionParams.z+_ProjectionParams.y))*_ProjectionParams.z, 0)











![[实用小知识]:Google浏览器添加代理SwitchyOmega](https://img-blog.csdnimg.cn/img_convert/49d5bb23ef59635bac069df8d1e276da.png)