题目
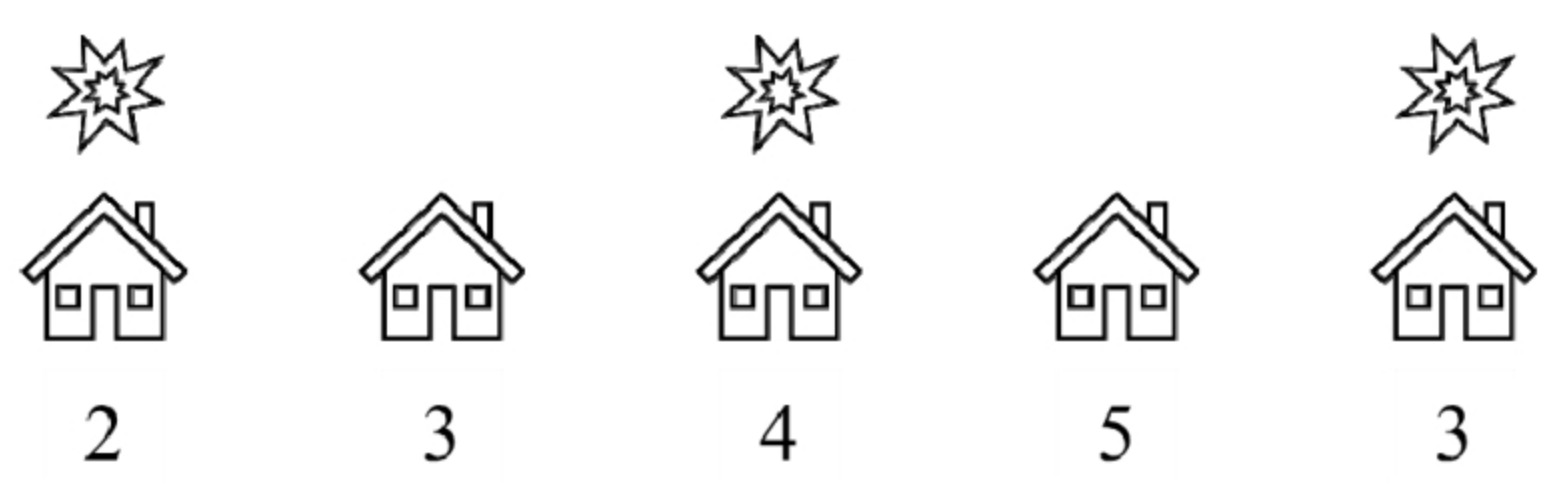
输入一个数组表示某条街道上的一排房屋内财产的数量。如果这条街道上相邻的两幢房屋被盗就会自动触发报警系统。请计算小偷在这条街道上最多能偷取到多少财产。例如,街道上5幢房屋内的财产用数组[2,3,4,5,3]表示,如果小偷到下标为0、2和4的房屋内盗窃,那么他能偷取到价值为9的财物,这是他在不触发报警系统的情况下能偷取到的最多的财物
分析
小偷在标号为i的房屋前有两个选择。一个选择是他进去偷东西。由于街道上有报警系统,因此他不能进入相邻的标号为i-1的房屋内偷东西,之前他最多能偷取的财物的最大值是f(i-2)。因此,小偷如果进入标号为i的房屋并盗窃,他最多能偷得f(i-2)+nums[i](nums是表示房屋内财物数量的数组)。另一个选择是小偷不进入标号为i的房屋,那么他可以进入标号为i-1的房屋内偷东西,因此此时他最多能偷取的财物的数量为f(i-1)。那么小偷在到达标号为i的房屋时他能偷取的财物的最大值就是两个选项的最大值,即f(i)=max(f(i-2)+nums[i],f(i-1)),这就是解决这个问题的状态转移方程。
上述状态转移方程有一个隐含条件,假设i大于或等于2。当i等于0时,f(0)是街道上只有标号为0的一幢房屋时小偷最多能偷得的财物的数量,此时他无所顾忌,直接进入标号为0的房屋偷东西,因此f(1)=nums[0];当i等于1时,f(1)是街道上只有标号为0和1的两幢房屋时小偷最多能偷得的财物的数量,因为街道上有报警系统,他只能到两幢房屋的其中一幢去偷东西,所以他应该选择到财物数量更多的房屋去偷东西,即f(1)=max(nums[0],nums[1])。
解: 带缓存的递归代码
public class Test {
public static void main(String[] args) {
int[] cost = {2, 3, 4, 5, 3};
int result = rob(cost);
System.out.println(result);
}
public static int rob(int[] nums) {
if (nums.length == 0) {
return 0;
}
int[] dp = new int[nums.length];
Arrays.fill(dp, -1);
helper(nums, nums.length - 1, dp);
return dp[nums.length - 1];
}
private static void helper(int[] nums, int i, int[] dp) {
if (i == 0) {
dp[i] = nums[0];
}
else if (i == 1) {
dp[i] = Math.max(nums[0], nums[1]);
}
else if (dp[i] < 0) {
helper(nums, i - 2, dp);// 为什么传i-2,因为最后知道需要dp[i-2]的值
helper(nums, i - 1, dp);// 为什么传i-1,因为最后知道需要dp[i-1]的值
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
}
}
}
分析2:空间复杂度为O(n)的迭代代码
也可以换一种思路,即先求出f(0)和f(1)的值,然后用f(0)和f(1)的值求出f(2),用f(1)和f(2)的值求出f(3),以此类推,直至求出f(n-1)。这种自下而上的思路通常可以用一个for循环实现
解
public class Test {
public static void main(String[] args) {
int[] cost = {2, 3, 4, 5, 3};
int result = rob(cost);
System.out.println(result);
}
public static int rob(int[] nums) {
if (nums.length == 0) {
return 0;
}
int[] dp = new int[nums.length];
dp[0] = nums[0];
if (nums.length > 1) {
dp[1] = Math.max(nums[0], nums[1]);
}
for (int i = 2; i < nums.length; i++) {
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
}
return dp[nums.length - 1];
}
}
分析3:空间复杂度为O(1)的迭代代码
如果仔细观察上述代码,就能发现计算“dp[i]”时只需要用到“dp[i-1]”和“dp[i-2]”这两个值,也就是说,只需要缓存两个值就足够了,并不需要一个长度为n的数组,因此,可以进一步优化代码的空间效率。
解
public class Test {
public static void main(String[] args) {
int[] cost = {2, 3, 4, 5, 3};
int result = rob(cost);
System.out.println(result);
}
public static int rob(int[] nums) {
if (nums.length == 0) {
return 0;
}
int[] dp = new int[2];
dp[0] = nums[0];
if (nums.length > 1) {
dp[1] = Math.max(nums[0], nums[1]);
}
for (int i = 2; i < nums.length; i++) {
dp[i % 2] = Math.max(dp[(i - 1) % 2], dp[(i - 2) % 2] + nums[i]);
}
return dp[(nums.length - 1) % 2];
}
}