【代码随想录】刷题笔记Day41

news2025/1/20 3:43:56

前言

早上的时间对我来说太重要了，效率很高，感觉是高中养成的习惯，但是就是睡太晚了，早上只有区区两个消失，感觉不够用啊，希望之后可以早点睡和早点起吧，就像大佬说的，人的身体是有开关的，早上是最好的时光，我就用这个时光来刷题~

62. 不同路径 - 力扣（LeetCode）

确定dp数组以及下标的含义：dp[i][j] 表示从(0,0)出发到(i, j) 有dp[i][j]条不同的路径。
确定递推公式：dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
dp数组的初始化：dp[i][0] = dp[0][j] = 1
遍历顺序：从左往右，从上往下

class Solution {
public:
    int uniquePaths(int m, int n) {
        int dp[m][n];
        // vector<vector<int>> dp(m, vector<int>(n, 0));
        for(int i = 0; i < m; i++) dp[i][0] = 1;
        for(int j = 0; j < n; j++) dp[0][j] = 1;
        for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
};

63. 不同路径 II - 力扣（LeetCode）

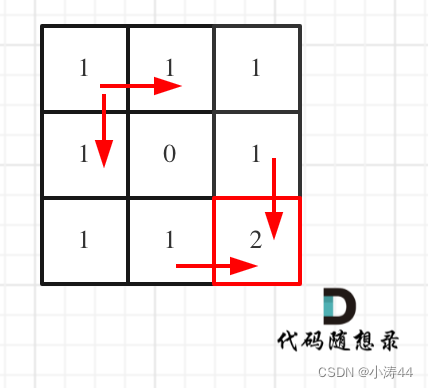
与上题不一样的点：递推公式要跳过障碍物，初始化障碍物及以后为0

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
	if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) //如果在起点或终点出现了障碍，直接返回0
            return 0;
        vector<vector<int>> dp(m, vector<int>(n, 0));
        for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
        for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (obstacleGrid[i][j] == 1) continue;
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
};

343. 整数拆分 - 力扣（LeetCode）

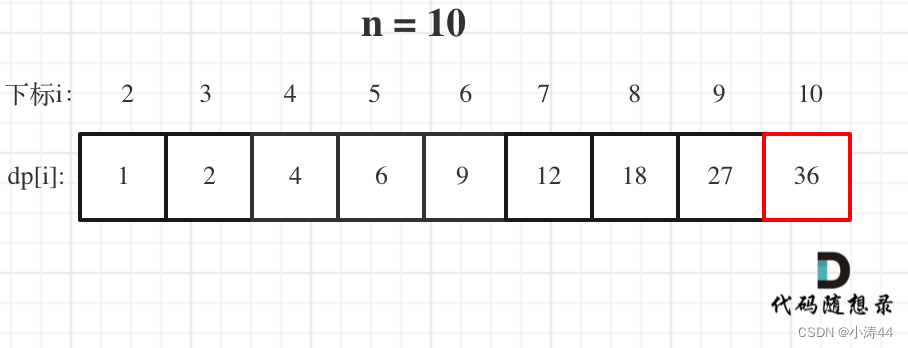
dp数组含义：dp[i]：分拆数字i，可以得到的最大乘积为dp[i]
递推公式：：dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});
初始化：dp[2] = 1；遍历顺序从前往后

class Solution {
public:
    int integerBreak(int n) {
        vector<int> dp(n + 1);
        dp[2] = 1;
        for (int i = 3; i <= n ; i++) {
            for (int j = 1; j <= i / 2; j++) {  // 取一半尽量相等相乘最大
                dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
                // 更新每个j的dp[i]，拆成j和i-j、拆成j和dp[i - j]
            }
        }
        return dp[n];
    }
};