- 论文链接:RePaint: Inpainting using Denoising Diffusion Probabilistic Models
- 代码链接:RePaint
Inpainting任务是指在任意一个二进制的掩码指定的图片区域上重新生成新的内容,且新生成的内容需要和周围内容保持协调。当前SOTA模型用单一类型的 mask 训练限制了模型的泛化能力,此外 pixel-wise 和 perceptual loss 会导致生成模型朝着纹理填充而不是语义修复方向更新。
本文提出了基于去噪扩散概率模型的图像修复方法Repaint,该方法甚至对于极端的 mask 情况(如mask 面积很大,几乎遮挡了整幅图像)都适用。本文利用一个预训练的 Unconditional DDPM 作为先验模型。为了调节生成过程,我们使用给定的图像信息仅对未屏蔽区域进行采样来改变反向扩散迭代。由于该技术不修改原始 DDPM 网络本身,因此该模型可以为任何修复形式生成高质量的图像。
1. 预备知识
本章节将介绍几个后面要用到的DDPM的结论,关于这些结论是如何得到的以及DDPM的相关知识可以移步至 通俗理解DDPM到Stable Diffusion原理。
扩散的前向过程:
q
(
x
t
∣
x
t
−
1
)
=
N
(
x
t
;
1
−
β
t
x
t
−
1
,
β
t
I
)
(1)
q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-\beta_t}x_{t-1},\beta_t\text{I})\quad\text{(1)}
q(xt∣xt−1)=N(xt;1−βtxt−1,βtI)(1)
进一步可以直接从
x
0
x_0
x0推到出加噪后的
x
t
x_t
xt:
q
(
x
t
∣
x
0
)
=
N
(
x
t
;
α
ˉ
t
x
0
,
(
1
−
α
ˉ
t
)
I
)
(
2
)
q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{\bar{\alpha}_t}x_0,(1-\bar{\alpha}_t)\mathbf{I})\quad(2)
q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I)(2)
反向降噪过程:
p
θ
(
x
t
−
1
∣
x
t
)
=
N
(
x
t
−
1
;
μ
θ
(
x
t
,
t
)
,
Σ
θ
(
x
t
,
t
)
)
(
3
)
p_\theta(x_{t-1}|x_t)=\mathcal{N}(x_{t-1};\mu_\theta(x_t,t),\Sigma_\theta(x_t,t))\quad(3)
pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))(3)
降噪过程就是通过神经网络来预测高斯分布的参数
μ
θ
(
x
t
,
t
)
\mu_\theta(x_t,t)
μθ(xt,t) 和
Σ
θ
(
x
t
,
t
)
)
\Sigma_\theta(x_t,t))
Σθ(xt,t))
2. 方法
使用
x
x
x 表示 ground truth 图像,那么
m
⊙
x
m\odot x
m⊙x 表示图像中被mask掉的未知区域,
(
1
−
m
)
⊙
x
(1-m)\odot x
(1−m)⊙x 表示剩余已知区域。那么根据(2)式的加噪过程,可以在任意时间点采样得到
t
t
t 时刻的已知区域
m
⊙
x
t
m\odot x_t
m⊙xt,如下图所示:

即:
x
t
−
1
known
∼
N
(
α
ˉ
t
x
0
,
(
1
−
α
ˉ
t
)
I
)
x_{t-1}^\text{known}\sim\mathcal{N}(\sqrt{\bar{\alpha}_t}x_0,(1-\bar{\alpha}_t)\mathbf{I})
xt−1known∼N(αˉtx0,(1−αˉt)I)
根据(3)式的降噪过程生成
t
t
t 时刻的未知区域
(
1
−
m
)
⊙
x
t
(1-m)\odot x_t
(1−m)⊙xt,如下图所示:

即:
x
t
−
1
unknown
∼
N
(
μ
θ
(
x
t
,
t
)
,
Σ
θ
(
x
t
,
t
)
)
x_{t-1}^\text{unknown}\sim\mathcal{N}(\mu_\theta(x_t,t),\Sigma_\theta(x_t,t))
xt−1unknown∼N(μθ(xt,t),Σθ(xt,t))
将以上两部分的结果相加即可得到
t
t
t 时刻的修复结果,如下图所示:
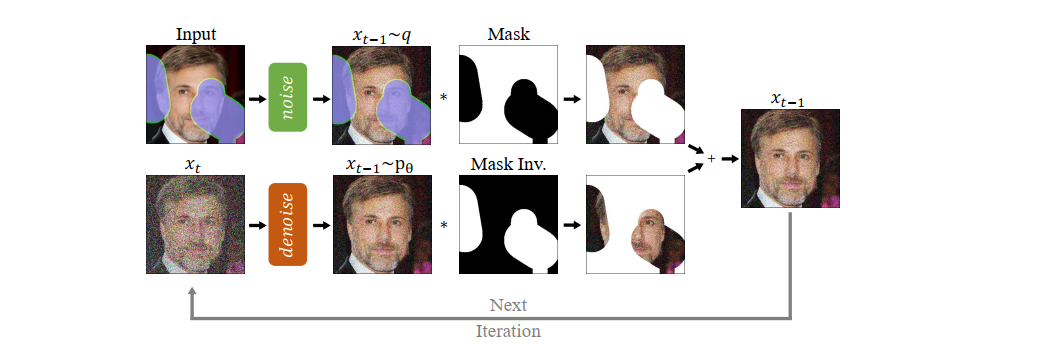
即:
x
t
−
1
=
m
⊙
x
t
−
1
known
+
(
1
−
m
)
⊙
x
t
−
1
unknown
x_{t-1}=m\odot x_{t-1}^\text{known}+(1-m)\odot x_{t-1}^\text{unknown}
xt−1=m⊙xt−1known+(1−m)⊙xt−1unknown
然后不断迭代下去,直到得到
x
0
x_0
x0.
Resampling技巧
当直接使用上述的方式进行Inpainting时,可以发现结果仅仅是修复的内容与已知区域匹配,但是语义并不正确。如下图所示,在
n
=
1
n=1
n=1时,修复的区域是比较粗糙的纹理和够的毛相匹配,但是语义并不正确。

造成上述问题的原因是模型在用DDPM输出的结果和已知区域的采样结果从
x
t
x_t
xt预测
x
t
−
1
x_{t-1}
xt−1时,使用(2)式对已知区域进行采样时并没有考虑到生成的部分。尽管模型尝试在降噪的每一步来协调图片,但是由于在每一步中都有上述相同问题,因此从来没有完全收敛。此外,在降噪的每一步中,由于方差策略
β
t
\beta_t
βt的减小,图片的改变也随着减小,因此模型在后续迭代中无法纠正错误。
针对上述分析的问题,作者提出 resampliing 的方法,即对模型的输出 x t x_t xt 重新根据(1)式将其扩散回到 x t x_t xt,并把重采样操作的次数称为 jump length,用 j j j 表示, j = 1 j=1 j=1 表示不进行重采样。
如下所示,展示了Repaint的伪代码

3. 实验结果
(1)定性结果

(2)定性结果2

(3)定量结果
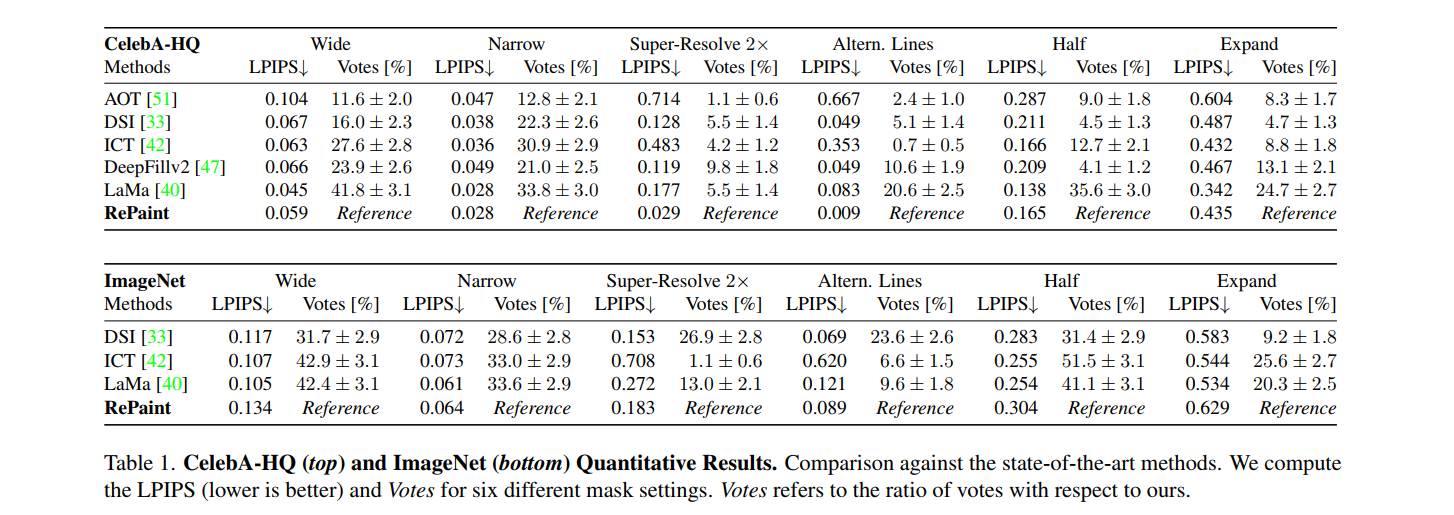
(3)降噪步数
T
T
T 和resampling步数
r
r
r 的关系