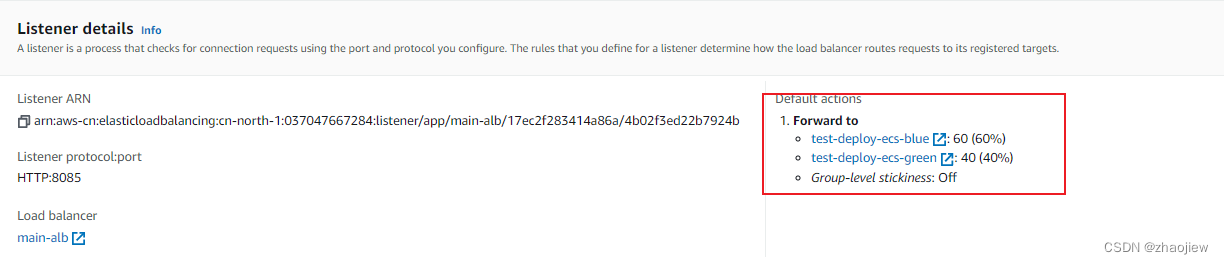
目录
合并集合
连通块中点的数量
蓝桥杯2017年第八届真题-合根植物
[蓝桥杯][2019年第十届真题] 修改数组
蓝桥幼儿园
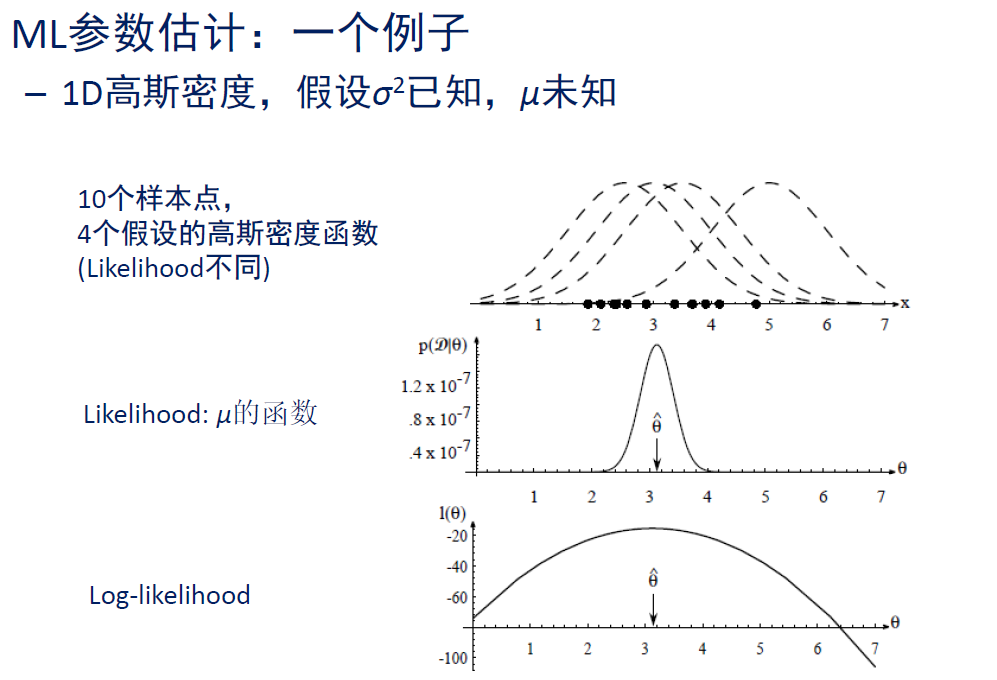
 刷了好多题,发现并查集这种思想挺妙的,是时候总结一下了;
刷了好多题,发现并查集这种思想挺妙的,是时候总结一下了;
作用与基本原理:

套路问题:

用一道模板题方便讲解;
合并集合


首先设置一个函数find();
find()函数的作用如问题2, 求集合的祖宗节点
(while(p[x]!=x) x=p[x] 如果不是根就找上一个,直到找到根为止)
元素合并操作:(元素也是集合)
开始时每个集合都是一个独立的集合,并且都是等于自己本身下标的数
例如:
p[5]=5,p[3]=3;
如果是M操作的话那么就将集合进行合并,合并的操作是:
p[3]=p[5]=5;
所以3的祖宗节点便成为了5,此时以5为祖宗节点的集合为{5,3}如果要将p[9]=9插入到p[3]当中,应该找到3的祖宗节点,然后再把p[9]=9插入其中,所以p[9]=find(3);(find()函数用于查找祖宗节点)
集合合并操作:
假设有以6为祖宗节点的集合为{6,4,7,10}。如果要将以6为祖宗节点的集合插入到以5为祖宗节点的集合,则该操作可以是p[6]=find(3)(或者find(9),find(5));
此时p[6]=5
当然如果是以6为祖宗节点集合中的4,7,10则可以这样
p[find(4)]=find(3)
总结:
合并操作:p[以a为祖宗节点的集合]=以b为祖宗节点的集合; (以a为祖宗节点的集合插到以b为祖宗节点的集合)
但是如果每次查找祖宗节点都要while一遍(while(p[x]!=x) x=p[x]),耗时大,于是就有了路径压缩;

int find(int x){
//祖先节点的父节点是自己本身
if(p[x] != x){
//将x置为x的祖先节点
p[x] = find(p[x]);
}
return p[x];
}路径压缩具体操作:
如图1
find(1) p[1] = 2 p[1] = find(2)
find(2) p[2] = 3 p[2] = find(3)
find(3) p[3] = 4 p[3] = find(4)
find(4) p[4] = 4 将p[4]返回于是一路回溯;4=p[4]=p[3]=p[2]=p[1];
注意只需要查找一遍,以后要用时间就是O(1)了
#include<iostream>
using namespace std;
int p[100010];
int find(int x)
{
if(p[x]!=x) p[x]=find(p[x]); //核心操作
return p[x];
}
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++) p[i]=i;
while(m--)
{
char op;
int a,b;
cin>>op>>a>>b;
if(op=='M') p[find(a)]=find(b); //集合合并
else
{
if(find(a)==find(b))
printf("Yes\n");
else
printf("No\n");
}
}
return 0;
}
总结:利用根相同特性查找集合
连通块中点的数量

AcWing 837. 连通块中点的数量 - AcWing
#include <iostream>
using namespace std;
const int N = 100010;
int n,m;
int p[N],cnt[N];
int find(int x)
{
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
p[i]=i;
cnt[i]=1; //将每个元素初始化为1
}
while(m--)
{
string op;
int a,b;
cin>>op;
if(op=="C")
{
cin>>a>>b;
a=find(a),b=find(b);
p[a]=b;
if(a!=b) //对不同集合合并才相加
{
cnt[b]+=cnt[a];
}
}
else if(op=="Q1")
{
cin>>a>>b;
if(find(a)==find(b)) puts("Yes");
else puts("No");
}
else
{
cin>>a;
cout<<cnt[find(a)]<<endl;
}
}
return 0;
}
总结:利用两个集合根不等特性相加求和
蓝桥杯2017年第八届真题-合根植物
w星球的一个种植园,被分成 m * n 个小格子(东西方向m行,南北方向n列)。每个格子里种了一株合根植物。
这种植物有个特点,它的根可能会沿着南北或东西方向伸展,从而与另一个格子的植物合成为一体。
如果我们告诉你哪些小格子间出现了连根现象,你能说出这个园中一共有多少株合根植物吗?
输入格式
第一行,两个整数m,n,用空格分开,表示格子的行数、列数(1<m,n<1000)。
接下来一行,一个整数k,表示下面还有k行数据(0<k<100000)
接下来k行,第行两个整数a,b,表示编号为a的小格子和编号为b的小格子合根了。
格子的编号一行一行,从上到下,从左到右编号。
比如:5 * 4 的小格子,编号:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
17 18 19 20
样例输入
5 4
16
2 3
1 5
5 9
4 8
7 8
9 10
10 11
11 12
10 14
12 16
14 18
17 18
15 19
19 20
9 13
13 17
样例输出
5
其合根情况参考下图:
如图所示,连一条线格子就少1,合并一次就将m*n减1一次,剩下的就是独立的
#include <iostream>
using namespace std;
int n,m,k;
int p[1000010];//要1e6 1000*1000
int find(int x)
{
return x==p[x]?x:p[x]=find(p[x]);
}
int main()
{
cin>>n>>m>>k;
int root=n*m;
for(int i=1;i<=root;i++) p[i]=i;
while(k--)
{
int a,b;
cin>>a>>b;
if(find(a)!=find(b))
{
p[find(a)]=find(b);
root--;
}
}
cout<<root;
return 0;
}总结:利用最多操作初始化次的特性(操作root次后就只剩一个集合,后续操作无效),求集合个数
[蓝桥杯][2019年第十届真题] 修改数组

可以用一个链表指向祖宗节点,比如输入2,链表中没有则让2指向3,输入1,链表中没有指向2,输入1链表中存在然后寻找1指向的祖宗节点为3此节点为3,然后让3指向4,输入3链表中存在然后此节点为4然后指向5,输入4,存在,此节点为5指向6。
#include <iostream>
using namespace std;
const int N=1e5+10;
int p[N];
int find(int x)
{
return x==p[x]?x:p[x]=find(p[x]);
}
int main()
{
int n;
cin>>n;
for(int i=1;i<=N;i++) p[i]=i;
for(int i=0;i<n;i++)
{
int m;
cin>>m;
m=find(m);
cout<<m<<" ";
p[m]++;
}
return 0;
}精选项目课程_IT热门课程_蓝桥云课课程 - 蓝桥云课
蓝桥幼儿园

输出描述
对于每个 op=2op=2 的输入,如果 xx 和 yy 是朋友,则输出一行 YES,否则输出一行 NO。
输入输出样例
输入
5 5
2 1 2
1 1 3
2 1 3
1 2 3
2 1 2
输出
NO
YES
YES
#include <iostream>
using namespace std;
int p[200010];
int find(int x)
{
return x==p[x]?x:p[x]=find(p[x]);
}
int main()
{
int n,m,op;
cin>>n>>m;
for(int i=1;i<=n;i++) p[i]=i;
while(m--)
{
int a,b;
cin>>op>>a>>b;
if(op==1) p[find(a)]=find(b);
else
{
if(find(a)==find(b))
cout<<"YES"<<endl;
else
cout<<"NO"<<endl;
}
}
return 0;
}结论:模板题,核心在于如何计算并套用;