补码
明明我们用正数用的更多,如果把0归到负数里面,那么正数就是整的2n次方了。
为什么不这么做呢?
如果你的手表快了20分钟,你可以:
1.把他调慢20分钟
2.再调快11小时40分钟
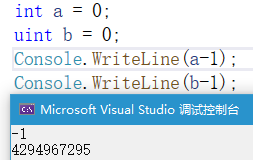
其实负数就是一个特别大的正数。CPU没有做出来减法这种电路。
所有的减法都是加上这个数的负数,然后用溢出来完成的。
并且使用这种方法储存数据,不需要把符号位单独拿出来算。只要跟着右边的比特一起算加法就行了。
因此,0只能划分到较小的正数那一块了。
二进制计数
计算机储存数字是以二进制方式储存的。
二进制的数字要么0,要么1。两个1加起来就会向前进位变成10。
列个表可以直观一点看出来
| - | - | - | - | - | - | - | - | - | - |
|---|---|---|---|---|---|---|---|---|---|
| 00000000(00) | 00000001(01) | 00000010(02) | 00000011(03) | 00000100(04) | 00000101(05) | 00000110(06) | 00000111(07) | 00001000(08) | 00001001(09) |
| 00001010(10) | 00001011(11) | 00001100(12) | 00001101(13) | 00001110(14) | 00001111(15) | 00010000(16) | 00010001(17) | 00010010(18) | 00010011(19) |
| 00010100(20) | 00010101(21) | 00010110(22) | 00010111(23) | 00011000(24) | 00011001(25) | 00011010(26) | 00011011(27) | 00011100(28) | 00011101(29) |
| 00011110(30) | 00011111(31) | 00100000(32) | 00100001(33) | 00100010(34) | 00100011(35) | 00100100(36) | 00100101(37) | 00100110(38) | 00100111(39) |
| 00101000(40) | 00101001(41) | 00101010(42) | 00101011(43) | 00101100(44) | 00101101(45) | 00101110(46) | 00101111(47) | 00110000(48) | 00110001(49) |
| 00110010(50) | 00110011(51) | 00110100(52) | 00110101(53) | 00110110(54) | 00110111(55) | 00111000(56) | 00111001(57) | 00111010(58) | 00111011(59) |
| 00111100(60) | 00111101(61) | 00111110(62) | 00111111(63) | 01000000(64) | 01000001(65) | 01000010(66) | 01000011(67) | 01000100(68) | 01000101(69) |
| 01000110(70) | 01000111(71) | 01001000(72) | 01001001(73) | 01001010(74) | 01001011(75) | 01001100(76) | 01001101(77) | 01001110(78) | 01001111(79) |
| 01010000(80) | 01010001(81) | 01010010(82) | 01010011(83) | 01010100(84) | 01010101(85) | 01010110(86) | 01010111(87) | 01011000(88) | 01011001(89) |
| 01011010(90) | 01011011(91) | 01011100(92) | 01011101(93) | 01011110(94) | 01011111(95) | 01100000(96) | 01100001(97) | 01100010(98) | 01100011(99) |
位逻辑运算
位与
| 左 | 右 | 输出 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1(只有两个数都是1时才输出1) |
34位与21的结果是
| 原数 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| 37 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 21 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 5 | 0 | 0 | 0 | 0 | 0 | 1(都为1) | 0 | 1(都为1) |
位或
逻辑与,是对每个比特进行一次与运算
| 左 | 右 | 输出 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1(只要有1就输出1) | 1 |
| 1(只要有1就输出1) | 0 | 1 |
| 1(只要有1就输出1) | 1 | 1 |
34位或21的结果是
| 原数 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| 37 | 0 | 0 | 1(有1就输出1) | 0 | 0 | 1(有1就输出1) | 0 | 1(有1就输出1) |
| 21 | 0 | 0 | 0 | 1(有1就输出1) | 0 | 1 | 0 | 1 |
| 53 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
异或
| 左 | 右 | 输出 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1(两数不同输出1) |
| 1 | 0 | 1(两数不同输出1) |
| 1 | 1 | 0 |
34位或21的结果是
| 原数 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| 37 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 21 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 48 | 0 | 0 | 1(两数不同) | 1(两数不同) | 0 | 0 | 0 | 0 |
反码
| 输入 | 输出 |
|---|---|
| 0 | 1(和输入不同) |
| 1 | 0(和输入不同) |
37的反码是
| 原数 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| 37 | 0(正数) | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| -38 | 1(负数) | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
全1的情况会被认为是-1。
而全0却会被认为是0。
所以一个数反码后绝对值会差1。
基本运算
加法
两个数字类型相加,和我们直接列竖式计算是一样的。
计算37+17,从上面的表找到对应的数字。
| 原数 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| 37 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 17 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 进位 | - | - | - | - | - | - | 1 | - |
| 54 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
加法自己身上的数,使用异或算法:两者不同则为1。
进位的数使用与算法:都为1才进位。
所以异或又称为不进位的加法。
减法
CPU没有算减法的指令,减法是计算加上他的负数完成的。
54-17,首先把17-1再进行反码
| 原数 | 8(符号位) | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| 17 | 0(正数) | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| -17 | 1(负数) | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
17这个负数,是和数字的最大值(全1)差16的数字。
进行相加后,
| 原数 | 9(溢出) | 8(符号位) | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|
| 54 | - | 0(正数) | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| -17 | - | 1(负数) | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 进位 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | - | - |
| 37 | 1(舍去) | 0(正数) | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
位移运算
位移运算就是把整个数字向一边挪。
不够的补0,溢出的舍去。
| 原数 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 37 | - | - | - | 0(正数) | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 4 | 0(正数) | 0 | 0 | 0 | 0 | 1 | 0 | 0 | - | - | - |