文章目录
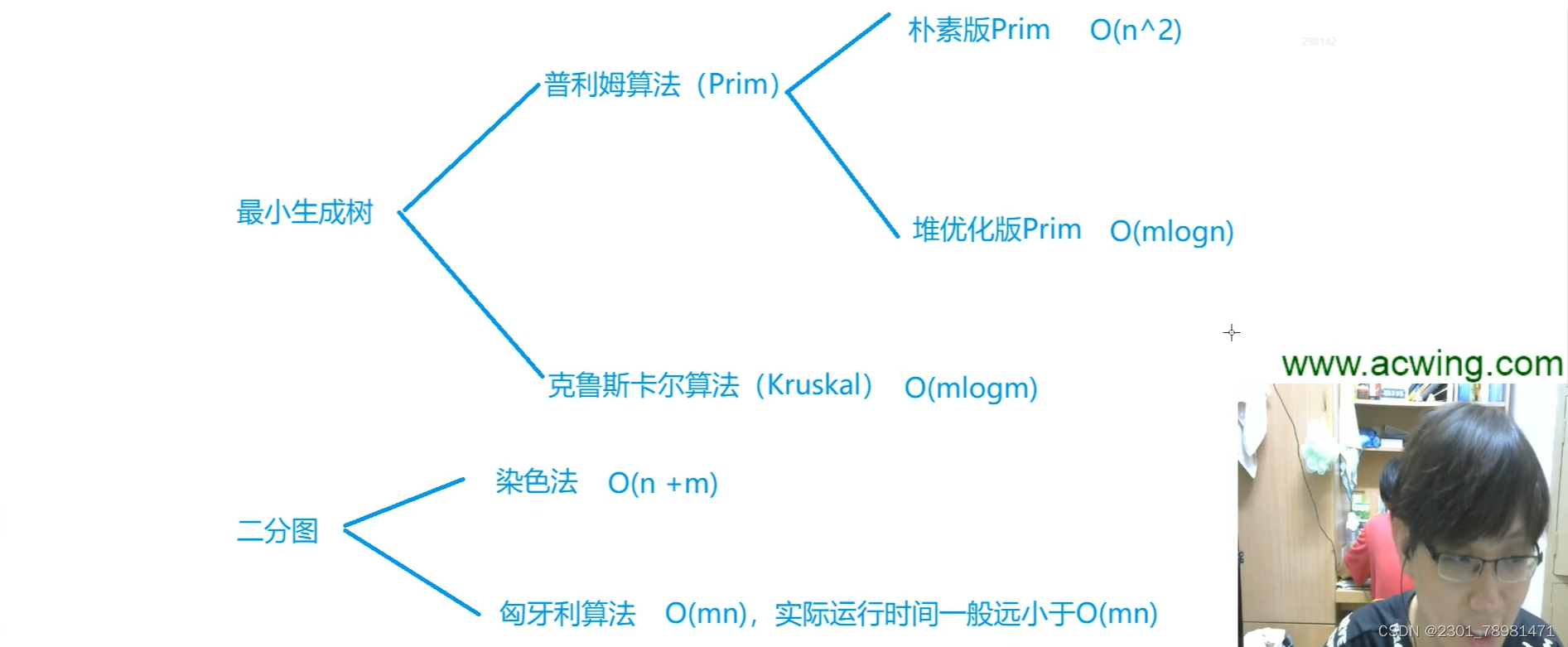
- 最小生成树概述
- P r i m Prim Prim 算法 - 稠密图 - O ( n 2 ) O(n^2) O(n2)
- 思路概述
- 时间复杂度分析
- AcWing 858. Prim算法求最小生成树
- CODE
- K r u s k a l Kruskal Kruskal 算法 - 稀疏图 - O ( m l o g m ) O(mlogm) O(mlogm)
- 思路解析
- 时间复杂度分析
- AcWing 859. Kruskal算法求最小生成树
- CODE
最小生成树概述
P r i m Prim Prim 算法 - 稠密图 - O ( n 2 ) O(n^2) O(n2)
思路概述
跟 D i j k s t r a Dijkstra Dijkstra 算法很相近,都是每个点轮一遍然后贪心找最小值,同样, P r i m Prim Prim 也可以用堆优化,但是不如 K r u s k a l Kruskal Kruskal 算法,所以不用。
- 用到三个数组:
g[][]邻接矩阵存边,st[]用于标记那些节点在生成树中,dist[]存储每个节点到生成树的最小距离。 - 首先,初始化每个点到生成树的距离,在一开始,除了根节点是 0 0 0,其他都是 I N F INF INF;
- 然后每个点轮一遍(因为生成树要每个点都在)
- 再次遍历,寻找到生成树最小的边连接的点,如果遍历完了发现最小值是 I N F INF INF,说明这个图不联通,没有最小生成树。
- 将这个点更新到生成树里去,累计生成树的边长,然后用这个点的值再更新一遍
dist[]数组。
时间复杂度分析
外层循环 n n n 次,内层是 2 n 2n 2n 次,所以是 O ( n ⋅ 2 n ) O(n·2n) O(n⋅2n),也就是 O ( n 2 ) O(n^2) O(n2)
AcWing 858. Prim算法求最小生成树
题目链接:https://www.acwing.com/activity/content/problem/content/924/。

CODE
#include <iostream> // 引入输入输出流库
#include <cstring> // 引入字符串处理库
#include <algorithm> // 引入算法库
using namespace std; // 使用标准命名空间
const int N = 520, INF = 0x3f3f3f3f; // 定义常量N和INF
int g[N][N]; // 定义邻接矩阵g
int dist[N]; // 定义距离数组dist
bool st[N]; // 定义状态数组st
int n, m; // 定义顶点数n和边数m
int prim(){ // 定义prim算法函数
memset(dist, 0x3f, sizeof dist); // 初始化dist数组
dist[1] = 0; // 将起点的距离设为0
int res = 0; // 初始化结果res
for(int i = 0; i < n; ++i){ // 遍历所有顶点
int t = -1; // 初始化t
for(int j = 1; j <= n; ++j) // 遍历所有顶点
if(!st[j] && (t == -1 || dist[t] > dist[j])) // 找到未被访问且距离最小的顶点
t = j;
if(dist[t] == INF) return INF; // 如果找不到顶点,返回INF
res += dist[t]; // 更新结果
st[t] = true; // 标记顶点t已被访问
for(int j = 1; j <= n; ++j) dist[j] = min(dist[j], g[j][t]); // 更新距离
}
return res; // 返回结果
}
int main() // 主函数
{
memset(g, 0x3f, sizeof g); // 初始化邻接矩阵g
cin >> n >> m; // 输入顶点数和边数
while (m -- ){ // 遍历所有边
int a, b, c;
scanf("%d%d%d", &a, &b, &c); // 输入边的两个顶点和权值
g[a][b] = g[b][a] = min(g[a][b], c); // 更新邻接矩阵
}
int t = prim(); // 调用prim算法
if(t == INF) puts("impossible"); // 如果返回INF,输出"impossible"
else printf("%d\n", t); // 否则输出结果
}
K r u s k a l Kruskal Kruskal 算法 - 稀疏图 - O ( m l o g m ) O(mlogm) O(mlogm)
思路解析
- 首先,将所有边按权值排序,这一步是 K r u s k a l Kruskal Kruskal 的瓶颈,复杂度是 O ( m ⋅ l o g m ) O(m·logm) O(m⋅logm)
- 接着初始化并查集,再把排序好的边轮一遍。
- 如果边的两个点的根节点不是同一个(两个节点没有全在树中),那就将两个点连起来,然后节点数和权重累积。
- 最后判断,如果生成树的边不是 n − 1 n - 1 n−1 条的话,说明图不联通,没有最小生成树。
时间复杂度分析
由上知排序瓶颈复杂度,然后是后面遍历每一条边的复杂度
O
(
m
)
O(m)
O(m),最后累计就是
O
(
m
l
o
g
m
)
O(mlogm)
O(mlogm)
但是由于排序的常数很小,所以实际运行时间比公式算出来要少的多。
AcWing 859. Kruskal算法求最小生成树
题目链接:https://www.acwing.com/activity/content/problem/content/925/

CODE
#include <iostream> // 引入输入输出流库
#include <cstring> // 引入字符串处理库
#include <algorithm> // 引入算法库
using namespace std; // 使用标准命名空间
const int N = 1e5 + 10, M = 2e5 + 10, INF = 0x3f3f3f3f; // 定义常量N、M和INF
int n, m; // 定义顶点数n和边数m
int p[N]; // 定义并查集数组p
struct edge{ // 定义边的结构体
int a, b, w;
}edges[M];
int find(int x){ // 定义并查集的查找函数
if(x != p[x]) p[x] = find(p[x]);
return p[x];
}
bool cmp(edge a, edge b){ // 定义比较函数,用于排序
return a.w < b.w;
}
int kruskal(){ // 定义kruskal算法函数
sort(edges, edges + m, cmp); // 对所有边按权值进行排序
for(int i = 1; i <= n; ++i) p[i] = i; // 初始化并查集
int res = 0, cnt = 0; // 初始化结果res和计数器cnt
for(int i = 0; i < m; ++i){ // 遍历所有边
int a = find(edges[i].a), b = find(edges[i].b), w = edges[i].w;
// 找到边的两个顶点的根节点和权值
if(a != b){ // 如果两个顶点不在同一个集合中
p[a] = b; // 合并两个集合
cnt++; // 计数器加1
res += w; // 更新结果
}
}
if(cnt < n - 1) return INF; // 如果生成树的边数小于n-1,返回INF
else return res; // 否则返回结果
}
int main() // 主函数
{
cin >> n >> m; // 输入顶点数和边数
for(int i = 0; i < m; ++i){ // 遍历所有边
int a, b, w;
scanf("%d%d%d", &a, &b, &w); // 输入边的两个顶点和权值
edges[i] = {a, b, w}; // 存储边
}
int t = kruskal(); // 调用kruskal算法
if(t == INF) puts("impossible"); // 如果返回INF,输出"impossible"
else printf("%d\n", t); // 否则输出结果
}