1.问题描述

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例 1：

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。

示例 2：

输入：nums1 = [1], m = 1, nums2 = [], n = 0
输出：[1]
解释：需要合并 [1] 和 [] 。
合并结果是 [1] 。

示例 3：

输入：nums1 = [0], m = 0, nums2 = [1], n = 1
输出：[1]
解释：需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意，因为 m = 0 ，所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。

提示：

• nums1.length == m + n
• nums2.length == n
• 0 <= m, n <= 200
• 1 <= m + n <= 200
• -109 <= nums1[i], nums2[j] <= 109

2.解题思路

1. 设置两个索引 i 和 j 分别指向 nums1 和 nums2 的有效元素的尾部，从它们的尾部开始向前遍历，同时设置索引 cur 指向 nums1 的最末尾

2. 在每次遍历过程中，比较 i 和 j 指向的元素值大小，把大的元素填充到 cur 的位置

3. 填充完毕说明那个元素已经放置在它应该放置的位置，不需要在管它了，把 cur 向前移动，同时把 i 或者 j 向前移动，继续比较 i 和 j 指向的元素值大小，把大的元素填充到 cur 的位置。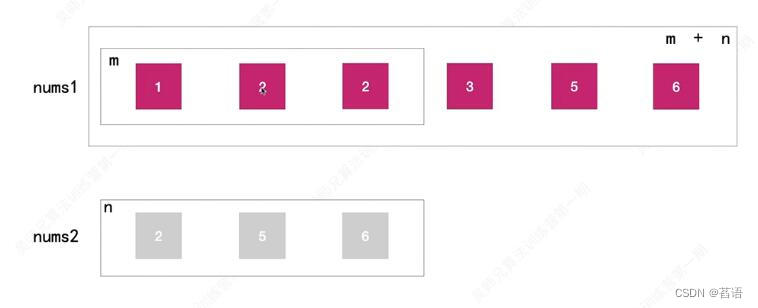

   

3.代码

python：

from typing import List


class Solution:
    def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> List[int]:
        # 索引从有序数组 nums1 有效元素的末端开始
        # 数组的下标索引从零开始计数
        # 索引   0    1     2
        # 数组 [ 1 ,  2  ,  3 ]
        i = m - 1

        # 索引从有序数组 nums2 的末端开始
        j = n - 1

        # 从有序数组 nums1 最末端的位置开始保存元素
        cur = m + n - 1

        # 通过循环把 num2 的元素都移动到 num1 中
        while j >= 0:

            # 比较 num1 和 num2 中当前的元素大小

            # 如果 num1 中的索引位置为 i 的元素大于 num2 中索引位置为 j 的元素
            # 为了防止越界 i 必须是大于等于 0
            if i >= 0 and nums1[i] > nums2[j]:

                # 把 num1 中的索引位置为 i 的元素复制到索引为 cur 的位置
                # 此时 cur 的元素已经确定下来
                nums1[cur] = nums1[i]

                # 接下来去确定 cur 前面一个元素应该放什么数字
                cur -= 1
                # 此时，索引 i 需要向前移动
                i -= 1
                # 否则，如果 num1 中的索引位置为 i 的元素小于或者等于 num2 中索引位置为 j 的元素
            else:

                # 把 num2 中的索引位置为 j 的元素复制到索引为 cur 的位置
                nums1[cur] = nums2[j]
                # 接下来去确定 cur 前面一个元素应该放什么数字
                cur -= 1
                # 此时，索引 j 需要向前移动
                j -= 1
        return nums1

solution = Solution()
nums1 = [1, 2, 3, 0, 0, 0]
m = 3
nums2 = [2, 5, 6]
n = 3  # 示例输入n
print(solution.merge(nums1, m, nums2, n))

C++：

#include<iostream>
#include <vector>
using namespace std;
class Solution {
	public:
		void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
			int i = m - 1;
			int j = n - 1;
			int cur = nums1.size() - 1;
			while( j >= 0  ) {
				if( i >=0 && nums1[i] > nums2[j] ) {
					nums1[cur] = nums1[i];
					cur--;
					i--;
				} else {
					nums1[cur] = nums2[j];
					cur--;
					j--;
				}
			}
		}
};

int main() {
    vector<int> nums1 = {1, 3, 5, 0, 0, 0}; 
    int m = 3;
    vector<int> nums2 = {2, 4, 6}; 
    int n = 3;
    
    Solution solution;
    solution.merge(nums1, m, nums2, n);
    
    cout << "Merged Array: ";
    for (int i = 0; i < nums1.size(); i++) {
        cout << nums1[i] << " ";
    }
    cout << endl;
    
    return 0;
}