LeetCode 2258. 逃离火灾：BFS

news2025/11/4 5:45:20

【LetMeFly】2258.逃离火灾

力扣题目链接：https://leetcode.cn/problems/escape-the-spreading-fire/

给你一个下标从 0 开始大小为 m x n 的二维整数数组 grid ，它表示一个网格图。每个格子为下面 3 个值之一：

0 表示草地。
1 表示着火的格子。
2 表示一座墙，你跟火都不能通过这个格子。

一开始你在最左上角的格子 (0, 0) ，你想要到达最右下角的安全屋格子 (m - 1, n - 1) 。每一分钟，你可以移动到相邻的草地格子。每次你移动之后，着火的格子会扩散到所有不是墙的相邻格子。

请你返回你在初始位置可以停留的最多分钟数，且停留完这段时间后你还能安全到达安全屋。如果无法实现，请你返回 -1 。如果不管你在初始位置停留多久，你总是能到达安全屋，请你返回 10⁹ 。

注意，如果你到达安全屋后，火马上到了安全屋，这视为你能够安全到达安全屋。

如果两个格子有共同边，那么它们为相邻格子。

示例 1：

输入：grid = [[0,2,0,0,0,0,0],[0,0,0,2,2,1,0],[0,2,0,0,1,2,0],[0,0,2,2,2,0,2],[0,0,0,0,0,0,0]]
输出：3
解释：上图展示了你在初始位置停留 3 分钟后的情形。
你仍然可以安全到达安全屋。
停留超过 3 分钟会让你无法安全到达安全屋。

示例 2：

输入：grid = [[0,0,0,0],[0,1,2,0],[0,2,0,0]]
输出：-1
解释：上图展示了你马上开始朝安全屋移动的情形。
火会蔓延到你可以移动的所有格子，所以无法安全到达安全屋。
所以返回 -1 。

示例 3：

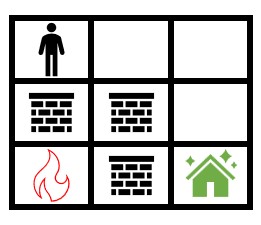
输入：grid = [[0,0,0],[2,2,0],[1,2,0]]
输出：1000000000
解释：上图展示了初始网格图。
注意，由于火被墙围了起来，所以无论如何你都能安全到达安全屋。
所以返回 10⁹ 。

提示：

m == grid.length
n == grid[i].length
2 <= m, n <= 300
4 <= m * n <= 2 * 10⁴
grid[i][j] 是 0 ，1 或者 2 。
grid[0][0] == grid[m - 1][n - 1] == 0

方法一：二分 + BFS

首先以所有的🔥为起点开始广度优先搜索，这样我们就能得到“火焰燃烧图”（🔥燃烧到某个坐标所需耗时）。

接着可以二分“👱的开局等待时长”。假设开局等待时间为 $t$ ，那么就从时间 $t$ 开始对👱能到达的位置进行广度优先搜索。

在对👱的广搜过程中：

若搜索到了“安全屋”的位置：若“👱的到达耗时小于等于🔥的到达耗时”，则表示👱能等待时间 $t$ 后再出发
否则（非安全屋位置）：若“👱的到达耗时小于🔥的到达耗时”，则表示人能到达该位置

以上，即可。

时间复杂度 $O(mn\log mn)$ ，其中 $size(grid)=m\times n$
空间复杂度 $O (mn)$

AC代码

C++

class Solution {
private:
    int m, n;
    int direction[4][2] = {{-1, 0}, {1, 0}, {0, 1}, {0, -1}};
    vector<vector<int>> fireTime;
    void debug(vector<vector<int>>& v) {
        for (auto& t : v) {
            for (auto& tt : t) {
                cout << tt << ' ';
            }
            cout << endl;
        }
    }

    void bfsFire(vector<vector<int>>& grid) {  // 计算火燃烧到每个位置时所需耗时并存入fireTime
        vector<vector<int>> graph = grid;
        fireTime = vector<vector<int>>(m, vector<int>(n, 1e9));
        queue<pair<int, int>> q;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (graph[i][j] == 1) {
                    q.push({i, j});
                    fireTime[i][j] = 0;
                }
            }
        }
        while (q.size()) {
            auto [x, y] = q.front();
            q.pop();
            for (int d = 0; d < 4; d++) {
                int tx = x + direction[d][0];
                int ty = y + direction[d][1];
                if (tx >= 0 && tx < m && ty >= 0 && ty < n && !graph[tx][ty]) {
                    graph[tx][ty] = 1;
                    fireTime[tx][ty] = fireTime[x][y] + 1;
                    q.push({tx, ty});
                }
            }
        }
    }

    bool check(vector<vector<int>>& grid, int t) {  // 其实是bfsPeople
        vector<vector<int>> peopleTime(m, vector<int>(n, 0)), graph(grid);
        peopleTime[0][0] = t;
        queue<pair<int, int>> q;
        q.push({0, 0});
        graph[0][0] = 2;
        while (q.size()) {
            auto [x, y] = q.front();
            q.pop();
            for (int d = 0; d < 4; d++) {
                int tx = x + direction[d][0];
                int ty = y + direction[d][1];
                int toTime = peopleTime[x][y] + 1;
                if (tx >= 0 && tx < m && ty >= 0 && ty < n && !graph[tx][ty]) {
                    graph[tx][ty] = 2;
                    if (tx == m - 1 && ty == n - 1 && toTime <= fireTime[m - 1][n - 1]) {
                        return true;
                    }
                    if (toTime < fireTime[tx][ty]) {
                        peopleTime[tx][ty] = toTime;
                        q.push({tx, ty});
                    }
                }
            }
        }
        return false;
    }
public:
    int maximumMinutes(vector<vector<int>>& grid) {
        m = grid.size(), n = grid[0].size();
        bfsFire(grid);
        int l = 0, r = n * m;
        int ans = -1;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if (check(grid, mid)) {
                ans = mid;
                l = mid + 1;
            }
            else {
                r = mid - 1;
            }
        }
        return ans >= n * m ? 1e9 : ans;
    }
};

Python

# from typing import List
# from copy import deepcopy

class Solution:
    def __init__(self) -> None:
        self.direction = [[-1, 0], [1, 0], [0, -1], [0, 1]]
    
    def bfsFire(self, grid: List[List[int]]) -> None:
        fireTime = [[int(1e9)] * self.n for _ in range(self.m)]
        graph = deepcopy(grid)
        q = []
        for i in range(self.m):
            for j in range(self.n):
                if graph[i][j] == 1:
                    q.append((i, j))
                    fireTime[i][j] = 0
        while q:
            x, y = q[0]
            q = q[1:]
            for dx, dy in self.direction:
                tx, ty = x + dx, y + dy
                if tx >= 0 and tx < self.m and ty >= 0 and ty < self.n and not graph[tx][ty]:
                    q.append((tx, ty))
                    fireTime[tx][ty] = fireTime[x][y] + 1
                    graph[tx][ty] = 1
        self.fireTime = fireTime
    
    def check(self, grid: List[List[int]], t: int) -> bool:
        if t == 4:
            print(self.fireTime)
        peopleTime = [[0] * self.n for _ in range(self.m)]
        graph = deepcopy(grid)
        q = []
        q.append((0, 0))
        graph[0][0] = 2
        peopleTime[0][0] = t
        while q:
            x, y = q[0]
            q = q[1:]
            thisTime = peopleTime[x][y] + 1
            for dx, dy in self.direction:
                tx, ty = x + dx, y + dy
                if tx >= 0 and tx < self.m and ty >= 0 and ty < self.n and not graph[tx][ty]:
                    graph[tx][ty] = 2
                    if tx == self.m - 1 and ty == self.n - 1 and thisTime <= self.fireTime[-1][-1]:
                        return True
                    if thisTime < self.fireTime[tx][ty]:
                        peopleTime[tx][ty] = thisTime
                        q.append((tx, ty))
        return False

    def maximumMinutes(self, grid: List[List[int]]) -> int:
        self.m, self.n = len(grid), len(grid[0])
        self.bfsFire(grid)
        l, r = 0, self.m * self.n
        ans = -1
        while l <= r:
            mid = (l + r) // 2
            if self.check(grid, mid):
                ans = mid
                l = mid + 1
            else:
                r = mid - 1
        return int(1e9) if ans >= self.m * self.n else ans

if __name__ == '__main__':
    print(Solution().maximumMinutes(
        [[0,2,0,0,0,0,0],
         [0,0,0,2,2,1,0],
         [0,2,0,0,1,2,0],
         [0,0,2,2,2,0,2],
         [0,0,0,0,0,0,0]])
    )
    """
    [[6, ∞, 4, 3, 2, 1, 2],
     [5, 4, 3, ∞, ∞, 0, 1],
     [6, ∞, 2, 1, 0, ∞, 2],
     [7, 8, ∞, ∞, ∞, 14, ∞],
     [8, 9, 10, 11, 12, 13, 14]]
    """