文章目录
- 第3章 时域分析法
- 3.1 基本概念
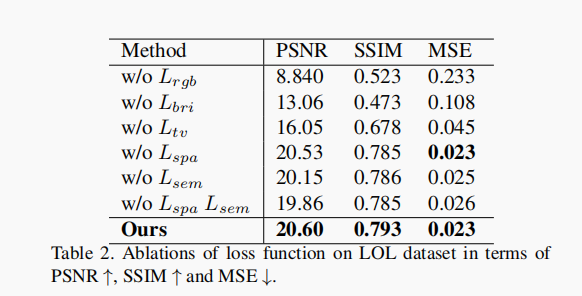
- 3.2~4 一阶、二阶、高阶系统的时间响应及动态性能
- 3.6 稳定性分析——==稳==
- 3.6.1. 稳定性的定义
- 3.6.2 稳定性的条件
- 3.6.3 劳斯稳定判据
- 首列出现0,但该行不全为0
- 首列出现0,且该行全为0
- 3.5 误差分析和计算——==准==
- 3.5.1稳态误差的基本概念
- 3.5.2稳态误差的计算
- (1)判定系统的稳定性
- (2)求误差传递函数
- (3)用终值定理求稳态误差
- 3.5.3稳态误差系数
- 3.5.4扰动引起的稳态误差和系统总误差
第3章 时域分析法
- 系统分析是指对系统的稳定性、误差和动态特性三方面的性能进行分析,即分析系统的稳定性、准确性和快速性。
- 稳定性:(基本要求)系统受扰动影响后能回到原来的平衡位置;
- 准确性:(稳态要求)稳态输出与理想输出间的误差(稳态误差)要小;
- 快速性:(动态要求)阶跃响应的过程要平稳、迅速。
- 建立了控制系统的数学模型后,就可以采用不同的方法来分析和研究控制系统。本文讨论的时域分析法就是其中的重要方法之一。
- 在时间域内,上述三方面的性能都可以通过求解描述控制系统的微分方程来获得,而微分方程的解则由控制系统的结构参数、初始条件以及输入信号所决定。
- 时域分析是指在时间域内研究系统在一定输入信号的作用下,其输出信号随时间的变化情况。
3.1 基本概念
3.2~4 一阶、二阶、高阶系统的时间响应及动态性能
参照前文:【自动控制原理】时域分析法:一阶、二阶、高阶系统的时间响应及动态性能
3.6 稳定性分析——稳
3.6.1. 稳定性的定义
-
若线性系统在任何初始扰动(或初始偏差)作用下,其动态过程随时间的推移逐渐衰减并趋于零,即恢复到原来平衡状态,则系统是稳定的,否则是不稳定的。

-
数学定义

-
稳定性是分析不存在外作用,仅在初始状态影响下系统的时间响应,也称为零输入响应
-
稳定性是控制系统自身的固有特性,它取决于系统本身的结构和参数,而与输入无关
3.6.2 稳定性的条件
系统所有特征根的实部是负数;所有根都位于复平面左半平面

3.6.3 劳斯稳定判据
线性定常系统稳定的充分必要条件是其特征根全部具有负实部。因此,判别系统的稳定性,就要解出系统特征方程的根,并检验这些特征根是否都具有负实部。但是,通过直接求解特征方程,并根据其特征根来分析系统稳定性的方法是不方便的。于是,就提出了这样的问题,是否可以不用直接求解特征方程的根,而是根据特征方程的根与系数的关系去判别系统的特征根是否全部具有负实部,并以此来分析系统的稳定性。回答是肯定的,而且为此形成了一系列的稳定性判据,其中最著名的一个判据是 1877 年由 E.J.Routh 提出的判据,称之为劳思稳定判据。这种判据是基于特征方程的根与系数的关系,通过特征方程的系数来直接判别系统的稳定性。
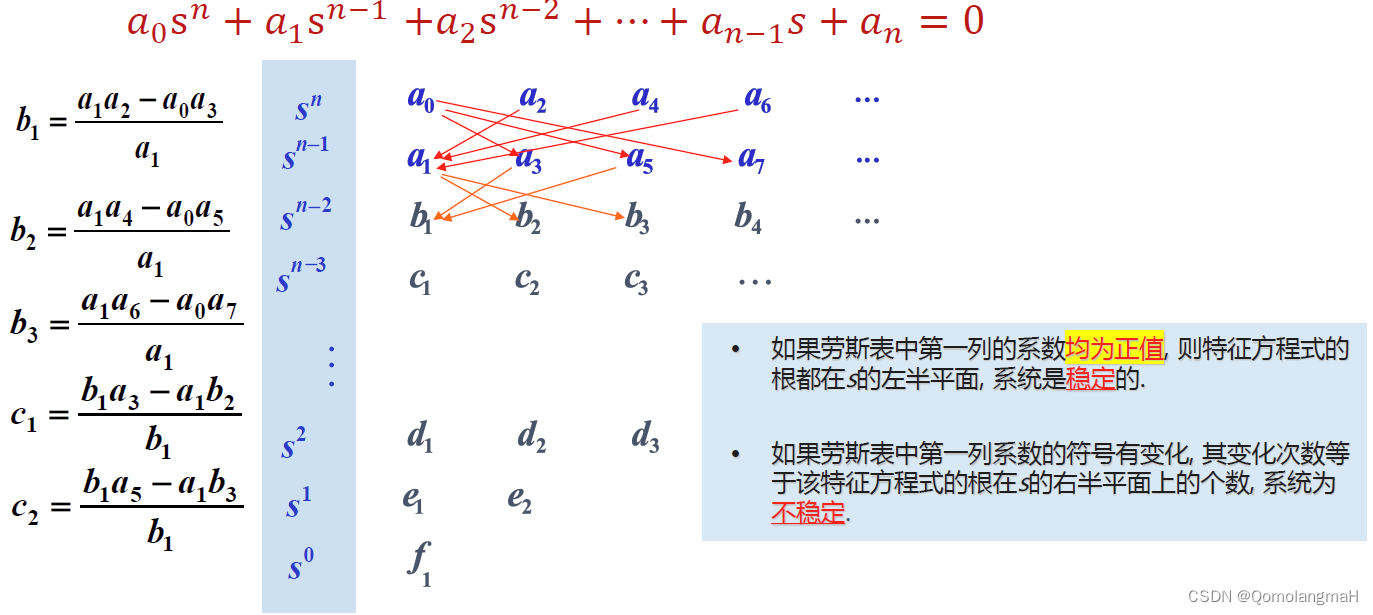

首列出现0,但该行不全为0


首列出现0,且该行全为0


3.5 误差分析和计算——准
3.5.1稳态误差的基本概念
- 控制系统性能
- 动态性能:
- 峰值时间tp:阶跃响应越过终值达到第一个峰值所需要的时间
- 超调量𝝈%:峰值超出终值的百分比
- 调节时间𝒕𝒔
- 稳态性能:稳态误差
- 动态性能:
e s s = l i m t ∞ = e ( ∞ ) e_{ss} = lim_{t\infty} =e(\infty) ess=limt∞=e(∞)
- 系统的误差分为动态误差和稳态误差,动态误差是指误差随时间变化的过程值。而稳态误差是指误差的终值
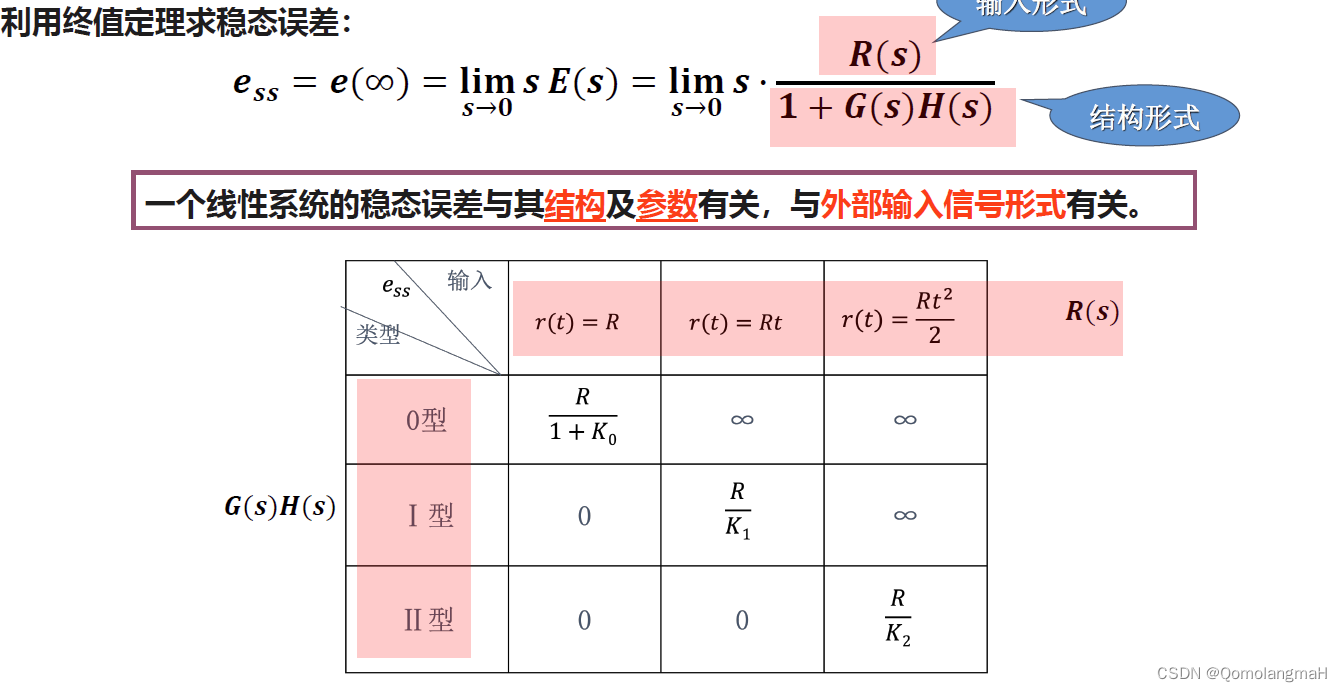
- 系统原理性稳态误差 :线性系统由于其结构、参数及输入信号形式不同所引起的稳态误差不同
3.5.2稳态误差的计算
计算稳态误差的一般步骤:
(1)判定系统的稳定性
向上看:3.6 稳定性分析
(2)求误差传递函数
参考前文:2.5 控制系统传递函数

(3)用终值定理求稳态误差