遍历二叉树算法描述

1.遍历定义：顺着某一条搜索路径寻访二叉树中的结点，使得每一个结点均被访问一次，而且仅访问一次（又称周游）。
2.遍历目的：得到树中所有结点的一个线性排列。
3.遍历用途：他是树结构插入，删除，修改，查找和排序算法的前提，是二叉树一切运算的基础和核心。
4.遍历方法：
依次遍历二叉树中的三个组成部分，便是便利了整个二叉树。
假设：L:遍历左子树，D：访问根结点，R：遍历右子树
则遍历整个二叉树方案共有：DLR,LDR,LRD,DRL,RDL,RLD六种。
若规定先左后右，则只有前三种情况：
DLR-----先根序遍历，
LDR-----中根序遍历
LRD-----后根序遍历

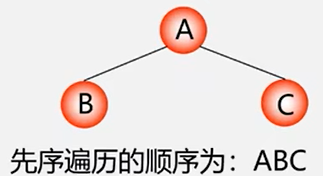
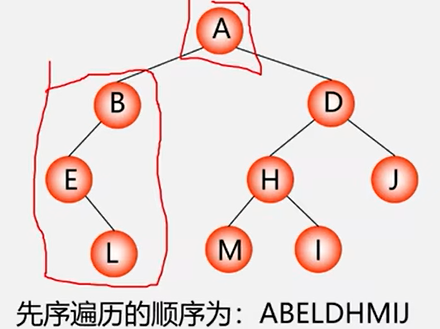
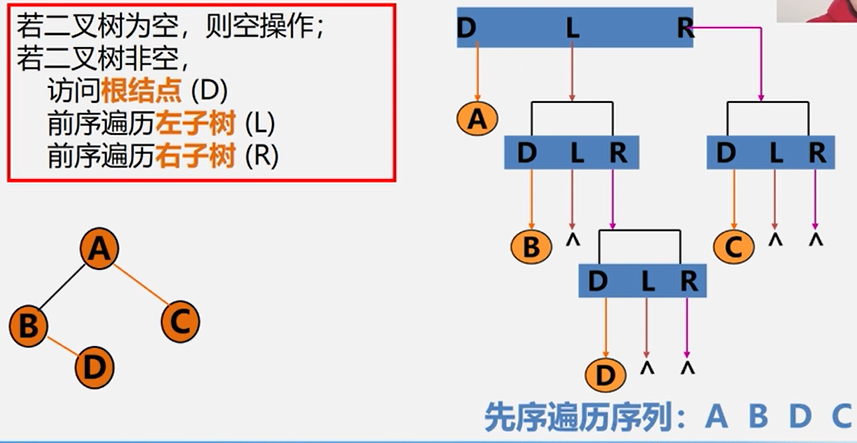
先序遍历二叉树的操作定义

若二叉树为空，则空操作，否则：
（1）访问根结点；
（2）先序遍历左子树；
（3）先序遍历右子树；

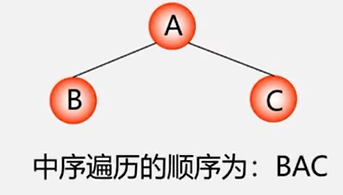
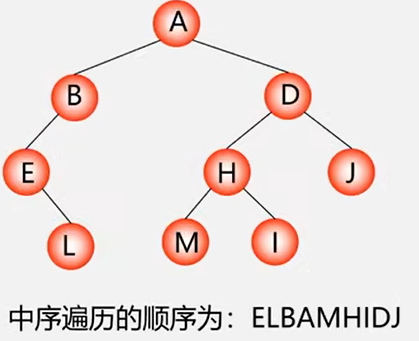
中序遍历二叉树的操作定义

若二叉树为空，则空操作，否则：
（1）先序遍历左子树；
（2）访问根结点；
（3）先序遍历右子树；

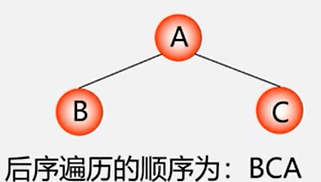
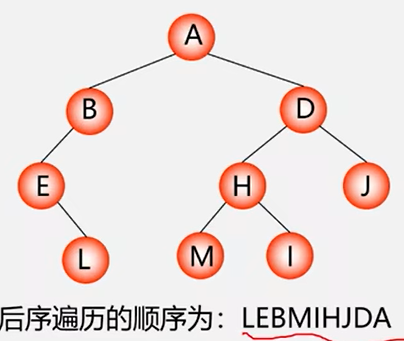
后序遍历二叉树的操作定义

若二叉树为空，则空操作，否则：
（1）先序遍历左子树；
（2）先序遍历右子树；
（3）访问根结点；


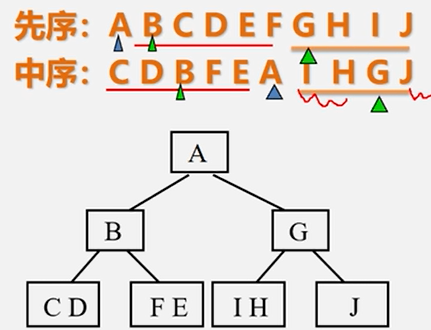
例题：已知二叉树的先序和中序序列，构造出相应的二叉树。




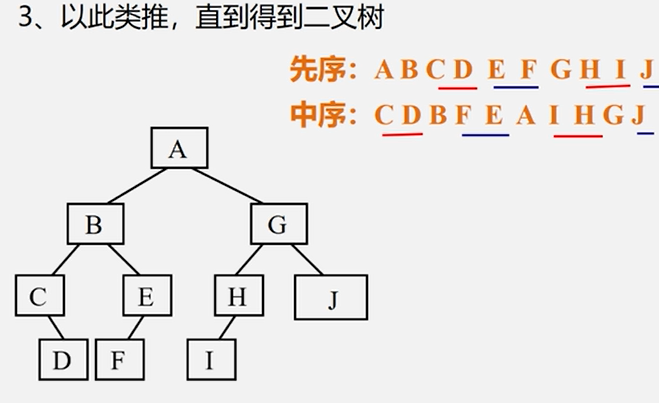
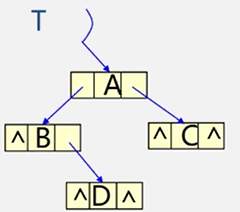
这里用到递归，将小的左子树右子树。

int PreOderTraverse(BiTree T) {
	if (T == NULL) {
		return 1;
	}
	else {
		cout << "输出T的头结点的值：" << T->data;
		PreOderTraverse(T->lchild);//递归调用左子树
		PreOderTraverse(T->rchild);//递归调用右子树
	}
}