---

前言

计数排序是一种 非比较排序。计数排序又称为 鸽巢原理 ，是对哈希直接定址法的变形应用。

---

一、计数排序算法核心思路

---

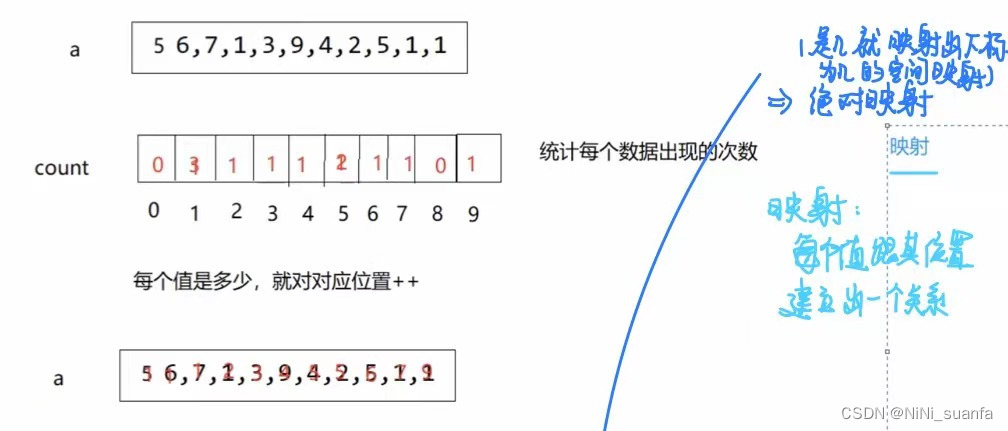
映射 概念补充

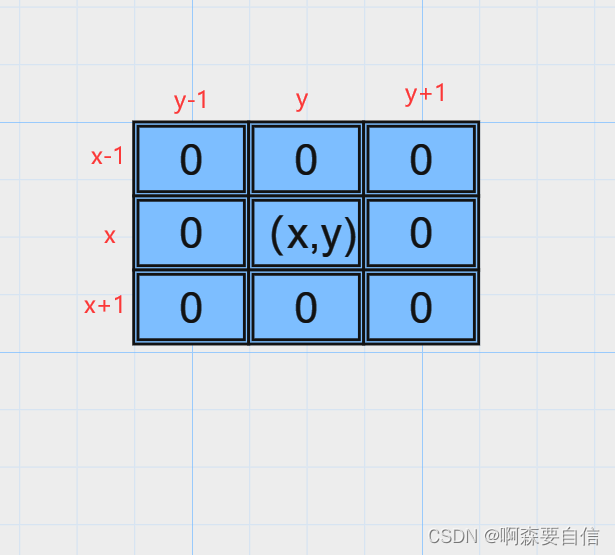
每个值跟其位置建立出一个关系

绝对映射

数值是几就映射出下标是几。如上图

若数组中数据的大小范围并不是乖乖的从0-1，那么这是再采用绝对映射，则会产生很大的空间浪费。

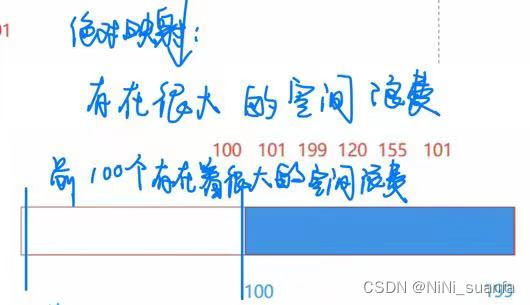
那么就有了相对映射的概念

相对映射

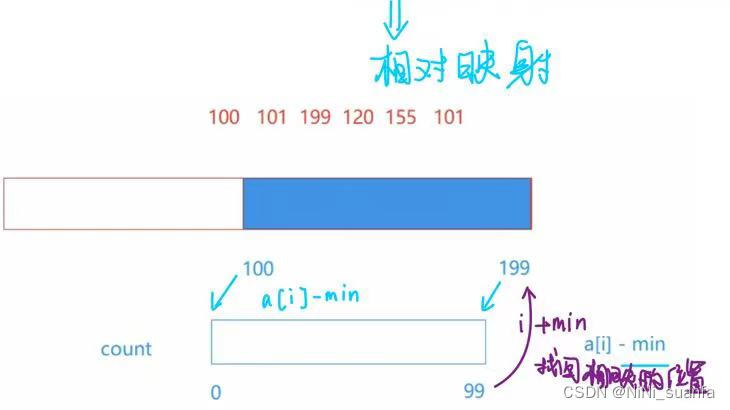
通过遍历原数组，找出min值，将 a[i] 的值 - min值 【即 a[ i ] - min 】就是对应 数组count[ ]的下标了，遍历到一个就令该下标（ 对应a[i]的值 ）下的 count [ ] 值++计数。

---

二、计数排序算法核心实现步骤

1. 遍历一遍数组 => 得出min和max值 => 确定数的范围

2. 确定范围 => 确定需要开辟的数组的大小

3. 开辟大小为range的空间count [ ] (避免了 绝对映射 那样的空间的浪费) 。用作统计 需排序的数组a[i] 中每个数据出现的次数。
   【注意：要进行初始化！！否则待会遍历计数数组中，那些并没有统计到有这个数出现的次数的位置，将以该内存原来的值（随机数）进行填入】

4. 遍历待排序的数组 => 统计数组中每个数据出现的次数 => 通过 a[i]-min 找到对应下标在 count 中的对应下标 => 对该下标的值对应++进行计数

5. 遍历计数数组，根据统计到的每个数的次数count[i]，就拷贝回去原数组count[i]次，i+min:对应回原数组中的值，while()循环覆盖原数组

---

三、码源详解

//计数排序——非比较排序
void CountSort(DataType* a,int n) {
    //遍历一遍数组 => 得出min和max值 => 确定数的范围
	int min = a[0]; int max = a[0];
	for (int i = 0; i < n; i++) {
		if (a[i] < min) {
			min = a[i];
		}
		if (max < a[i]) {
			max = a[i];
		}
		//确定范围 => 确定需要开辟的数组的大小
		int range = max - min + 1;    //[min,max]左闭右闭，所以+1

		//开辟大小为range的空间，避免了 绝对映射 那样的空间的浪费
		DataType* count = (DataType*)malloc(sizeof(DataType)*range);
		if (count == NULL) {
			perror("malloc fail");
			exit(-1);
		}
		//内存重置 将count数组中的值都初始化为0，重置数组大小为sizeof(DataType) * range
		//要进行初始化，否则待会遍历计数数组中，那些并没有统计到有这个数出现的次数的位置，将以该内存原来的值（随机数）进行填入
		memset(count, 0, sizeof(DataType) * range);

		                                        //数组中的值
		//遍历数组 => 统计数组中各数据出现的次数 => 通过 a[i]-min 找到对应下标在 count 中的对应下标 => 对该下标的值对应++进行计数
		for (i = 0; i < n; i++) {
			count[a[i] - min]++;
		}

		//排序
		//遍历计数数组，根据统计到的每个数的次数count[i]，就拷贝回去原数组count[i]次，覆盖原数组
		//遍历数组
		int j = 0;     //放外面，遍历a[] j记录的数值 不会别被清
		for (i = 0; i < range; i++) {
		while (count[i]--){             //count[i]=0的进不了循环
			a[j++] = i + min;             //i+min:对应回原数组中的值
		}
		}
	  }
}

---

四、效率分析

总体特点：比较小众

1. 适用于数据范围相对集中。
2. 只适合整形
3. 基数排序

（1）时间复杂度 — O（Max（N，range））

（2）空间复杂度 — O（range）