0-1背包 完全背包 + 至多/恰好/至少 + 空间优化 + 常见变形题（实战力扣题）

news2025/5/24 1:10:52

（一）01背包  

1.回溯三问

  • dfs(i,c) = max(dfs(i-1,c),dfs(i-1,c-w[i])+v[i])
# capacity:背包容量
# w[i]: 第 i 个物品的体积
# v[i]: 第 i 个物品的价值
# 返回:所选物品体积和不超过 capacity 的前提下，所能得到的最大价值和
def zero_one_knapsack(capacity:int,w:List[int],v:List[int]) -> int:
    n = len(w)
    @cache #记忆化搜索 
    def dfs(i,c):
        if i < 0:
            return 0
        if c < w[i]:
            return dfs(i-1,c)
        return max(dfs(i-1,c),dfs(i-1,c-w[i])+v[i])
    return dfs(n-1,capacity)

 2.常见变形

 3.实战力扣题 

494. 目标和 - 力扣（LeetCode）

给你一个非负整数数组 nums 和一个整数 target 。向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，可以构造一个 表达式 ：

  • 例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，在 1 之前添加 '-' ，然后串联起来得到表达式 "+2-1" 。

返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

>>思考和分析： 

  • 正数和:p       
  • 负数和:s-p
  • p-(s-p) = t     
  • 2p=s+t
  • 化简可得: p=(s+t)/2

（1）记忆化搜索

class Solution:
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        target += sum(nums)
        if target < 0 or target%2: # 负数 or 奇数
            return 0 # 方案数为0
        target //= 2
        n = len(nums)
        # 记忆化搜索
        @cache
        def dfs(i,c):
            if i < 0:
                return 1 if c==0 else 0
            if c < nums[i]:
                return dfs(i-1,c)
            return dfs(i-1,c)+dfs(i-1,c-nums[i])
        return dfs(n-1,target)

（2）1:1 翻译成递推

  • dfs(i,c) = dfs(i-1,c) + dfs(i-1,c-w[i])

  • f[i][c] = f[i-1][c] + f[i-1][c-w[i]]

  • f[i+1][c] = f[i][c] + f[i][c-w[i]]

class Solution:
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        target += sum(nums)
        if target < 0 or target%2: # 负数 or 奇数
            return 0 # 方案数为0
        target //= 2
        n = len(nums)
        # 二维dp
        f = [[0]*(target+1)for _ in range(n+1)]
        f[0][0] = 1

        for i,x in enumerate(nums):
            for c in range(target+1):
                if c<x:
                    f[i+1][c] = f[i][c]
                else:
                    f[i+1][c] = f[i][c] + f[i][c-x]
        return f[n][target]
  • 优化空间

方式一：二维数组优化

  • f[(i+1)%2][c] = f[i%2][c] + f[i%2][c-w[i]]
class Solution:
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        # 二维dp
        f = [[0]*(target+1)for _ in range(2)]
        f[0][0] = 1

        for i,x in enumerate(nums):
            for c in range(target+1):
                if c<x:
                    f[(i+1)%2][c] = f[i%2][c]
                else:
                    f[(i+1)%2][c] = f[i%2][c] + f[i%2][c-x]
        return f[n%2][target]

方式二：一维数组优化

  • f[i+1][c] = f[i][c] + f[i][c-w[i]]
  • f[c]=f[c]+f[c-w[i]]

class Solution:
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        target += sum(nums)
        if target < 0 or target%2: # 负数 or 奇数
            return 0 # 方案数为0
        target //= 2

        n = len(nums)

        # 一维dp
        f = [0]*(target+1)
        f[0] = 1

        for x in nums:
            for c in range(target,x-1,-1):
                f[c] = f[c] + f[c-x]
        return f[target]

拓展：问题思考(O_O)?如果题目改成至多为 target，该怎么修改呢？

  • 「恰好」改成「至多」 
# 恰好
class Solution:
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        ...
        ...
        ...
        # 记忆化搜索
        @cache
        def dfs(i,c):
            if i < 0:
                return 1 if c==0 else 0 # 边界条件：由于要求是恰好组成。恰好情况：当c=0的时候，才能返回1，表示这是一个合法的方案；
            if c < nums[i]:
                return dfs(i-1,c)
            return dfs(i-1,c)+dfs(i-1,c-nums[i])
        return dfs(n-1,target)


改成如下：

# 至多
class Solution:
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        ...
        ...
        ...
        # 记忆化搜索
        @cache
        def dfs(i,c):
            if i < 0:
                return 1 // 至多情况：不用判断c == 0 的情况
            if c < nums[i]:
                return dfs(i-1,c)
            return dfs(i-1,c)+dfs(i-1,c-nums[i])
        return dfs(n-1,target)
# 恰好
class Solution:
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        ...
        ...
        ...

        # 一维dp
        f = [0]*(target+1)
        f[0] = 1

        for x in nums:
            for c in range(target,x-1,-1):
                f[c] = f[c] + f[c-x]
        return f[target]

改成如下：

# 至多
class Solution:
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        ...
        ...
        ...

        n = len(nums)

        # 一维dp
        f = [1]*(target+1) # 把这里全都初始化成1

        for x in nums:
            for c in range(target,x-1,-1):
                f[c] = f[c] + f[c-x]
        return f[target]
  •  「恰好」改成「至少」
# 恰好
class Solution:
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        ...
        ...
        ...
        # 记忆化搜索
        @cache
        def dfs(i,c):
            if i < 0:
                return 1 if c==0 else 0 # 边界条件：由于要求是恰好组成。恰好情况：当c=0的时候，才能返回1，表示这是一个合法的方案；
            if c < nums[i]:
                return dfs(i-1,c)
            return dfs(i-1,c)+dfs(i-1,c-nums[i])
        return dfs(n-1,target)


改成如下：

# 至少
class Solution:
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        ...
        ...
        ...
        # 记忆化搜索
        @cache
        def dfs(i,c):
            if i < 0:
                return 1 if c<=0 else 0 // 至少情况：c<=0
            return dfs(i-1,c)+dfs(i-1,c-nums[i])
        return dfs(n-1,target)
# 恰好
class Solution:
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        ...
        ...
        ...

        # 一维dp
        f = [0]*(target+1)
        f[0] = 1

        for x in nums:
            for c in range(target,x-1,-1):
                f[c] = f[c] + f[c-x]
        return f[target]

改成如下：

# 至少
class Solution:
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        ...
        ...
        ...

        n = len(nums)

        # 一维dp
        f = [0]*(target+1)
        f[0] = 1

        for x in nums:
            for c in range(target,-1,-1):
                f[c] = f[c] + f[max(c-x,0)] # 表示把所有 c<=0 的状态 都记录到 f[0] 里面
        return f[target]

target=0 的情况下，每个物品都可以 「选」 或者 「不选」，那么一共有 2^{n} 种方案，刚好这种写法可以从 1 开始，算出来  2^{n}（这句话我听得迷迷糊糊的，有小伙伴懂得指导我一下_(:з」∠)_）

 （二）完全背包  

1.回溯三问

  • dfs(i,c) = max(dfs(i-1,c),dfs(i,c-w[i])+v[i])
# capacity:背包容量
# w[i]: 第 i 个物品的体积
# v[i]: 第 i 个物品的价值
# 每种物品可以无限次重复选
# 返回:所选物品体积和不超过 capacity 的前提下，所能得到的最大价值和
def unbounded_knapsack(capacity:int,w:List[int],v:List[int]) -> int:
    n = len(w)
    @cache
    def dfs(i,c):
        if i < 0:
            return 0
        if c < w[i]:
            return dfs(i-1,c)
        return max(dfs(i-1,c),dfs(i,c-w[i])+v[i])
    return dfs(n-1,capacity)

（1）01背包和完全背包的递归式对比：

  • dfs(i,c) = max(dfs(i-1,c),dfs(i-1,c-w[i])+v[i])
  • dfs(i,c) = max(dfs(i-1,c),dfs(i,c-w[i])+v[i])

【重点】在选了一个物品之后，i 是不变的，表示你可以继续选第 i 种物品，所以这里不是递归到 i-1，而是 i

2.常见变形

3.实战力扣题 

322. 零钱兑换 - 力扣（LeetCode）

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。你可以认为每种硬币的数量是无限的。

（1）记忆化搜索

class Solution:
    # 边界条件：由于要求是恰好组成 amount,所以和上一题一样
    # 当c=0的时候，才能返回0，表示这是一个合法的方案；否则就应该返回无穷大，表示这是一个不合法的方案
    # 这样后面去min的时候就自然的取到了不是无穷大的那个方案（硬币个数）
    # 如果ans小于inf，表示这是一个合法的方案，否则一个合法的方案都没有
    def coinChange(self, coins: List[int], amount: int) -> int:
        n = len(coins)
        @cache
        def dfs(i,c):
            if i < 0:
                return 0 if c==0 else inf
            if c < coins[i]:
                return dfs(i-1,c)
            return min(dfs(i-1,c),dfs(i,c-coins[i])+1)
        ans = dfs(n-1,amount)
        return ans if ans<inf else -1

（2）1:1 翻译成递推

  • dfs(i,c) = min(dfs(i-1,c),dfs(i,c-w[i])+v[i])

  • f[i][c] = min(f[i-1][c],f[i][c-w[i]]+v[i])

  • f[i+1][c] = min(f[i][c],f[i+1][c-w[i]]+v[i])

class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        n = len(coins)
        # 数组的初始值：根据递归的边界条件，可知当i=0,c=0，才是0；其它的都是无穷大
        # 步骤：1:直接把数组初始化成无穷大 2.把f[0][0]改成0就好了
        f=[[inf] * (amount+1) for _ in range(n+1)]
        f[0][0] = 0
        for i,x in enumerate(coins):
            for c in range(amount+1):# 强调一下，c 表示剩余容量
                if c<x:
                    f[i+1][c] = f[i][c]
                else:
                    f[i+1][c] = min(f[i][c],f[i+1][c-x]+1)
        ans = f[n][amount]
        return ans if ans < inf else -1
  • 优化空间

方式一：二维数组优化

  • f[(i+1)%2][c] = min(f[i%2][c],f[(i+1)%2][c-w[i]]+v[i])
class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        n = len(coins)
        # 数组的初始值：根据递归的边界条件，可知当i=0,c=0，才是0；其它的都是无穷大
        # 步骤：1:直接把数组初始化成无穷大 2.把f[0][0]改成0就好了
        f=[[inf] * (amount+1) for _ in range(2)]
        f[0][0] = 0
        for i,x in enumerate(coins):
            for c in range(amount+1):# 强调一下，c 表示剩余容量
                if c<x:
                    f[(i+1)%2][c] = f[i%2][c]
                else:
                    f[(i+1)%2][c] = min(f[i%2][c],f[(i+1)%2][c-x]+1)
        ans = f[n%2][amount]
        return ans if ans < inf else -1

方式二：一维数组优化

  • f[i+1][c] = min(f[i][c],f[i+1][c-w[i]]+v[i])
  • f[c] = min(f[c],f[c-w[i]]+v[i])

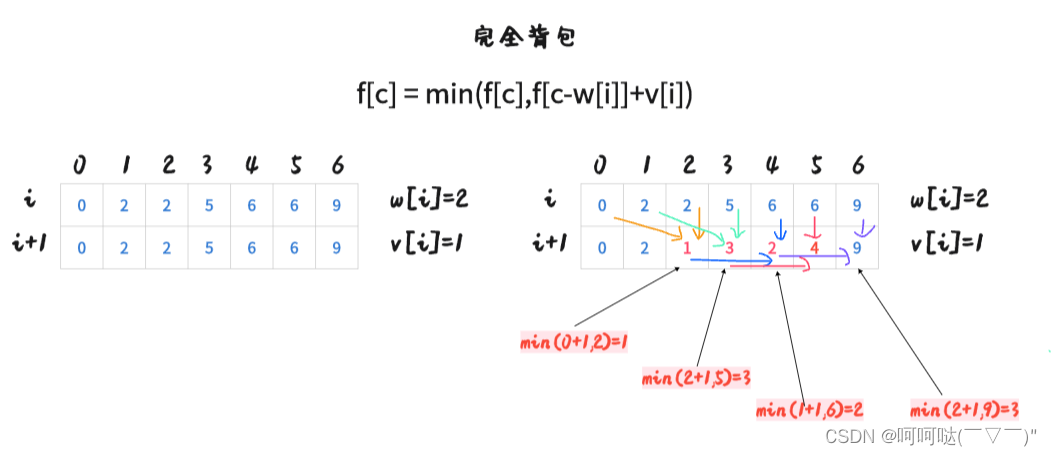
  • 需要注意：在恰好装满的情况下，这个数组它不一定是个有序数组 
class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        n = len(coins)

        f=[inf] * (amount+1) 
        f[0] = 0
        for x in coins:
            for c in range(x,amount+1):
                    f[c] = min(f[c],f[c-x]+1)
        ans = f[amount]
        return ans if ans < inf else -1

总结一下循环顺序的问题(O_O)?

  • 如果你在写一个不是背包的DP问题，但是得到了类似的状态转移方程，那么要怎么思考循环的顺序呢？

实战篇：这篇文章就是得到了类似的状态转移方程，用上图来思考循环顺序

LCR 166.珠宝的最高价值 + 动态规划 + 记忆化搜索 + 递推 + 空间优化-CSDN博客icon-default.png?t=N7T8https://blog.csdn.net/weixin_41987016/article/details/134207574?spm=1001.2014.3001.5501

参考和推荐视频：

0-1背包 完全背包【基础算法精讲 18】_哔哩哔哩_bilibiliicon-default.png?t=N7T8https://www.bilibili.com/video/BV16Y411v7Y6/?spm_id_from=333.788&vd_source=a934d7fc6f47698a29dac90a922ba5a3

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1170016.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

安装虚拟机后ifconfig不显示IP地址及设置静态IP地址ssh连接

安装虚拟机后ifconfig不显示IP地址及设置静态IP地址ssh连接

ifconfig不显示IP地址 可以看到ens160并没有显示IP地址&#xff0c;刚刚装好的虚拟机是很干净的&#xff0c;连网卡都没有&#xff0c;我们修改一个配置文件&#xff1a; vim /etc/sysconfig/network-scripts/ifcfg-ens160将文件中的onboot修改为yes&#xff0c;即启动时需不需…
阅读更多...
数字频带传输——多进制数字调制及MATLAB仿真

数字频带传输——多进制数字调制及MATLAB仿真

文章目录 前言一、MASK&#xff08;一维信号&#xff09;1、MASK 简介2、MASK 矢量表示 二、MPSK&#xff08;二维信号&#xff09;1、MPSK 简介2、MPSK 矢量表示 三、MQAM&#xff08;二维信号&#xff09;1、MQAM 简介2、MQAM 信号的矢量表示 四、正交 MFSK&#xff08;M维信…
阅读更多...
YB2503HV 100V 3A SOP8内置MOS 高效率降压IC(昱灿）

YB2503HV 100V 3A SOP8内置MOS 高效率降压IC(昱灿）

YB2503HV 100V 3A SOP8内置MOS 高效率降压IC 描述&#xff1a; YB2503HV是单片集成可设定输出电流的开关型降压恒压驱动器&#xff0c;可工作在宽输入电压范围具有优良的负载和线性调整度。安全保护机制包括每周期的峰值限流、软启动、过压保护和温度保护。YB2503HV需要非常少…
阅读更多...
5W2H分析法：全面思考和解决问题的实用工具

5W2H分析法：全面思考和解决问题的实用工具

5W2H分析法又叫七问分析法&#xff0c;创于二战中美国陆军兵器修理部。发明者用五个以W开头的英语单词和两个以H开头的英语单词进行设问&#xff0c;发现解决问题的线索&#xff0c;寻找发明思路&#xff0c;进行设计构思&#xff0c;从而搞出新的发明项目。5W2H简单、方便&…
阅读更多...
速拿offer，超全自动化测试面试题+答案汇总，背完还怕拿不到offer？

速拿offer，超全自动化测试面试题+答案汇总，背完还怕拿不到offer？

目录&#xff1a;导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结&#xff08;尾部小惊喜&#xff09; 前言 1、你会封装自动化…
阅读更多...
手机上有哪些支持设置农历日期提醒的工具

手机上有哪些支持设置农历日期提醒的工具

很多人的生日都是按照农历日期来安排的&#xff0c;而农历日期和公历日期相错的日子很多&#xff0c;在手机上如果想要记录农历生日提醒&#xff0c;需要借助一些支持设定农历日期的工具来实现。 手机上有哪些支持设置农历日期提醒的工具呢&#xff1f;敬业签是一款可以在手机…
阅读更多...
高斯过程回归 | 高斯过程回归（Gaussian Process Regression）

高斯过程回归 | 高斯过程回归（Gaussian Process Regression）

高斯过程回归（Gaussian Process Regression）是一种非参数的回归方法，它基于高斯过程模型来建模数据的分布情况。在高斯过程回归中，假设数据点之间的关系服从多元高斯分布。 具体来说，考虑有一组输入变量X和对应的输出变量Y，我们希望通过这些已知数据点来建立一个模型，进…
阅读更多...
K8S知识点（一）

K8S知识点（一）

&#xff08;1&#xff09;应用部署方式转变 &#xff08;2&#xff09;K8S介绍 容器部署容易出现编排问题&#xff0c;为了解决就出现了大量的编排软件&#xff0c;这里将的是K8S编排问题的解决佼佼者 弹性伸缩&#xff1a;当流量从1000变为1200可以&#xff0c;自动开启一个…
阅读更多...
关于编程语言，开发者眼中的争论与共识

关于编程语言，开发者眼中的争论与共识

点击文末“阅读原文”即可参与节目互动 剪辑、音频 / 卷圈 运营 / SandLiu 卷圈 监制 / 姝琦 封面 / 姝琦Midjourney 产品统筹 / bobo 场地支持 / 声湃轩北京录音间 联合制作 / RTE开发者社区 xxx 是最好的编程语言&#xff01;此话一出&#xff0c;必能掀起一场技术圈儿…
阅读更多...
python图像处理 ——图像锐化

python图像处理 ——图像锐化

python图像处理 ——图像锐化 前言一、原理二、 空间域锐化滤波1.拉普拉斯算子&#xff08;Laplacian&#xff09;2.罗伯茨算子&#xff08;Roberts&#xff09;3.Sobel算子4.Prewitt算子5.Scharr算子 三、实验对比 前言 由于收集图像数据的器件或传输图像的通道存在一些质量缺…
阅读更多...
pip install -r requirements.txt

pip install -r requirements.txt

挂了梯子报错 不挂梯子gg下
阅读更多...
橙河网络：坏人是怎么形成的？

橙河网络：坏人是怎么形成的？

小A是一个非常热心的人&#xff0c;给谁帮忙&#xff0c;都免费。 大家都说&#xff0c;小 A&#xff0c;实在人呀&#xff0c;哈哈。 小B搬来了&#xff0c;他活多&#xff0c;弄不过来&#xff0c;常找小 A 来帮忙。 小A 每次来帮忙&#xff0c;小B 都给小A一张大团结(100…
阅读更多...
SpringBoot集成Swagger接口文档/测试

SpringBoot集成Swagger接口文档/测试

文章目录 Swagger 介绍Swagger 使用常用注解 Swagger 介绍 使用 Swagger 你只需要按照它的规范去定义接口及接口相关的信息&#xff0c;就可以做到生成接口文档&#xff0c;以及在线接口调试页面。官网&#xff1a;https://swagger.io/ Knife4j 是为 Java MVC 框架集成 Swagg…
阅读更多...
【Python】列表、集合、字典基础知识

【Python】列表、集合、字典基础知识

列表 列表中元素的类型可以不同&#xff0c;列表内部存储方式是元素值存储在不连续的空间&#xff0c;但是把他们的指针存在一块连续的空间 列表的创建 1.list1[] 创建一个空列表 2.用list函数 3.split函数截取 列表的更新 1.通过索引[]改变 2.切片修改 3.列表方法更新 列表…
阅读更多...
SLAM从入门到精通（参数标定）

SLAM从入门到精通（参数标定）

【 声明&#xff1a;版权所有&#xff0c;欢迎转载&#xff0c;请勿用于商业用途。 联系信箱&#xff1a;feixiaoxing 163.com】 标定是slam开发过程中很重要的一个环节。这部分内容涉及到很多方面&#xff0c;比如说传感器、比如说算法、比如说机械&#xff0c;总之好的标定不…
阅读更多...
C3P0、DBCP、Druid 三种数据库连接池的使用

C3P0、DBCP、Druid 三种数据库连接池的使用

文章目录 数据库连接池1 C3P0 数据库连接池2 DBCP 数据库连接池3 Druid 数据库连接池 数据库连接池 JDBC 的数据库连接池使用 javax.sql.DataSource 来表示&#xff0c;DataSource 只是一个接口&#xff0c;该接口通常由服务器(Weblogic, WebSphere, Tomcat)提供实现&#xff…
阅读更多...
SpringCloudTencent(上)

SpringCloudTencent(上)

SpringCloudTencent 1.PolarisMesh介绍2.北极星具备的功能3.北极星包含的组件4.功能特性1.服务管理1.服务注册2.服务发现3.健康检查 2.配置管理 5.代码实战1.环境准备2.服务注册与发现3.远程调用 1.PolarisMesh介绍 1.北极星是腾讯开源的服务治理平台&#xff0c;致力于解决分…
阅读更多...
Dev-C调试的基本方法2-1

Dev-C调试的基本方法2-1

在Dev-C中调试程序&#xff0c;首先需要在程序中设置断点&#xff0c;之后以调试的方式运行程序。 1 设置断点 当以调试的方式运行程序时&#xff0c;程序会在断点处停下来。点击要设置断点代码行号左侧部分&#xff0c;此时会有如图1所示的红点和绿色对勾&#xff0c;表示断…
阅读更多...
Mybatis与Mybatis-Plus(注解与Xml)(单表与多表)

Mybatis与Mybatis-Plus(注解与Xml)(单表与多表)

准备工作 这里我们准备了两个与数据库表对应的实体类&#xff0c;stu为学生表&#xff0c;cls为班级表 类属性上的注解如 TableId等 为Mybatis-Plus的注解&#xff0c;使用mybatis会无视掉这些注解 在Stu 类的最后一个属性我们定义了Cls实体类的对象&#xff0c;对于单表查询&…
阅读更多...
使用php打印时间精确到毫秒及毫秒转成11位时间戳

使用php打印时间精确到毫秒及毫秒转成11位时间戳

在PHP中&#xff0c;可以使用microtime函数来获取当前时间&#xff0c;包括毫秒。以下是示例代码&#xff1a; // 获取当前时间戳&#xff08;秒&#xff09; $time microtime(true); // 将当前时间戳转换为毫秒 $milliseconds round($time * 1000); // 输出当前时间&#…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023