文章目录
- 前言
- 一、MASK(一维信号)
- 1、MASK 简介
- 2、MASK 矢量表示
- 二、MPSK(二维信号)
- 1、MPSK 简介
- 2、MPSK 矢量表示
- 三、MQAM(二维信号)
- 1、MQAM 简介
- 2、MQAM 信号的矢量表示
- 四、正交 MFSK(M维信号)
- 1、正交 MFSK 简介
- 2、M 进制正交信号的矢量表示
- 五、MATLAB 仿真
- 1、MATLAB 源码
- 2、仿真及结果
前言
数字频带信号通常也称为数字调制信号,其信号频谱通常是带通型的,适合于在带通型信道中传输。数字调制是将基带数字信号变换成适合带通型信道传输的一种信号处理方式,正如模拟通信中的一样,可以通过对基带信号的频谱搬移来适应信道特性,也到同样的目的可以采用频率调制、相位调制的方式来达到同样的目的。
本文将主要通过 Matlab 来学习多进制的调制解调方式,包括 QPSK、OQPSK,并分析和仿真这些调制系统在 AWGN 信道下的性能。
一、MASK(一维信号)
1、MASK 简介
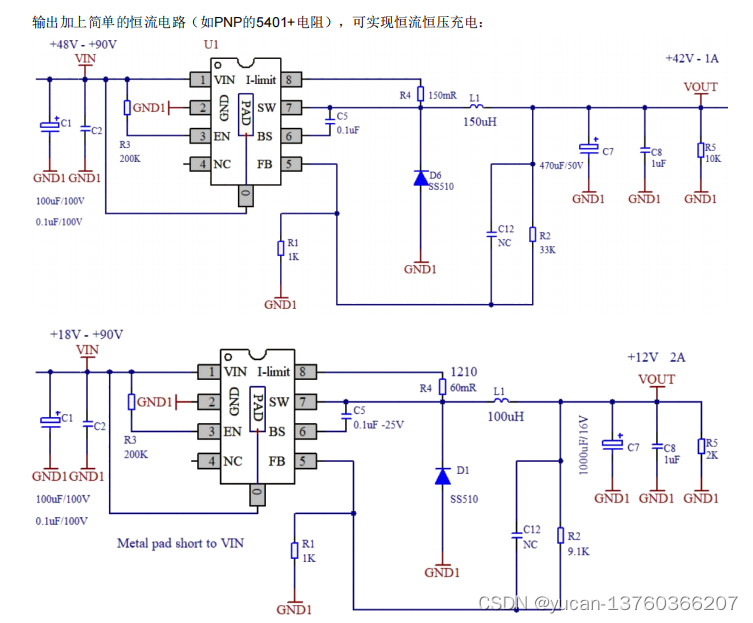
MASK 信号将 M 进制数字符号一一映射为 M 个幅度值不同的波形,可以写成如下形式:
s
m
(
t
)
=
A
m
g
(
t
)
c
o
s
2
π
f
c
t
(
m
=
1
,
2
,
.
.
.
,
M
,
0
≤
t
≤
T
s
)
s_m(t)=A_mg(t)cos2\pi f_ct \hspace{0.5cm} (m=1,2,...,M,0\le t\le T_s)
sm(t)=Amg(t)cos2πfct(m=1,2,...,M,0≤t≤Ts)
这里 {
A
m
,
1
≤
m
≤
M
A_m,1\le m\le M
Am,1≤m≤M} 与M进制符号一一对应,一般
M
=
2
k
M=2^k
M=2k,且
A
m
=
(
2
m
−
1
−
M
)
d
A_m=(2m-1-M)d
Am=(2m−1−M)d,
m
=
1
,
2
,
.
.
.
,
M
m=1,2,...,M
m=1,2,...,M,
g
(
t
)
g(t)
g(t) 是基带成形信号。
2、MASK 矢量表示
s
m
(
t
)
=
s
m
f
(
t
)
s_m(t)=s_mf(t)
sm(t)=smf(t)
其中,
f
(
t
)
=
2
ε
g
g
(
t
)
c
o
s
2
π
f
c
t
f(t)=\sqrt{\frac{2}{\varepsilon_g}}g(t)cos2\pi f_ct
f(t)=εg2g(t)cos2πfct,(
∫
−
∞
∞
f
2
(
t
)
d
t
=
1
\int_{-\infty}^{\infty}f^2(t)dt=1
∫−∞∞f2(t)dt=1),
s
m
=
A
m
ε
g
/
2
s_m=A_m \sqrt{\varepsilon_g/2}
sm=Amεg/2,
(
m
=
1
,
2
,
.
.
.
M
)
(m=1,2,...M)
(m=1,2,...M),这里
ε
g
=
∫
−
∞
∞
g
2
(
t
)
d
t
\varepsilon_g=\int_{-\infty}^{\infty}g^2(t)dt
εg=∫−∞∞g2(t)dt。
因此,MASK信号可以用一维信号空间中的点(星座)表示,如下图示意了 8ASK 的星座图。

二、MPSK(二维信号)
1、MPSK 简介
MPSK 信号将 M进制符号与 M 个载波相位一一对应,可以写成如下形式:
s
m
(
t
)
=
g
(
t
)
c
o
s
2
π
M
(
m
−
1
2
)
c
o
s
2
π
f
c
t
−
g
(
t
)
s
i
n
2
π
M
(
m
−
1
2
)
s
i
n
2
π
f
c
t
s_m(t)=g(t)cos\frac{2\pi}{M}(m-\frac{1}{2})cos2\pi f_ct-g(t)sin\frac{2\pi}{M}(m-\frac{1}{2})sin2\pi f_ct
sm(t)=g(t)cosM2π(m−21)cos2πfct−g(t)sinM2π(m−21)sin2πfct
2、MPSK 矢量表示
s
m
(
t
)
=
s
m
1
f
1
(
t
)
+
s
m
2
f
2
(
t
)
s_m(t)=s_{m1}f_1(t)+s_{m2}f_2(t)
sm(t)=sm1f1(t)+sm2f2(t)
其中:
f
1
(
t
)
=
2
ε
g
g
(
t
)
c
o
s
2
π
f
c
t
f_1(t)=\sqrt{\frac{2}{\varepsilon_g}}g(t)cos2\pi f_ct
f1(t)=εg2g(t)cos2πfct,
f
2
(
t
)
=
−
2
ε
g
g
(
t
)
s
i
n
2
π
f
c
t
f_2(t)=-\sqrt{\frac{2}{\varepsilon_g}}g(t)sin2\pi f_ct
f2(t)=−εg2g(t)sin2πfct,
∫
−
∞
∞
f
1
(
t
)
f
2
(
t
)
d
t
=
0
\int_{-\infty}^{\infty}f_1(t)f_2(t)dt=0
∫−∞∞f1(t)f2(t)dt=0
s m 1 = ε g 2 c o s 2 π M ( m − 1 2 ) s_{m1}=\sqrt{\frac{\varepsilon_g}{2}}cos\frac{2\pi}{M}(m-\frac{1}{2}) sm1=2εgcosM2π(m−21), s m 2 = ε g 2 s i n 2 π M ( m − 1 2 ) s_{m2}=\sqrt{\frac{\varepsilon_g}{2}}sin\frac{2\pi}{M}(m-\frac{1}{2}) sm2=2εgsinM2π(m−21)
s m = [ s m 1 , s m 2 ] s_m=[s_{m1},s_{m2}] sm=[sm1,sm2], m = 1 , 2 , . . . M m=1,2,...M m=1,2,...M, E s = ε g / 2 E_s=\varepsilon_g/2 Es=εg/2
因此,MPSK 可以用二维空间中的星座点表示,下图示意了 QPSK 调制的星座图
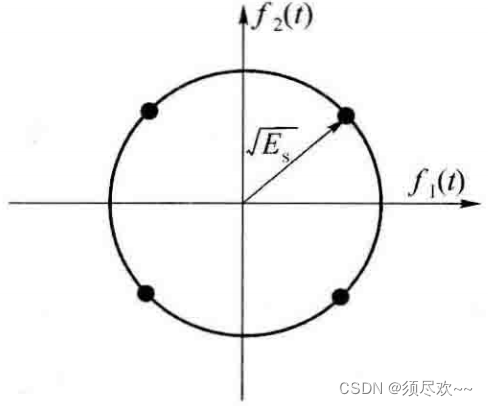
三、MQAM(二维信号)
1、MQAM 简介
用载波的不同幅度、相位对应 M 进制符号,则可以得到 QAM (正交幅度调制)信号,可以写成:
s
m
(
t
)
=
A
c
g
(
t
)
c
o
s
2
π
f
c
t
−
A
s
g
(
t
)
s
i
n
2
π
f
c
t
,
0
≤
t
≤
T
s
s_m(t)=A_cg(t)cos2\pi f_ct-A_sg(t)sin2\pi f_ct,0\le t \le T_s
sm(t)=Acg(t)cos2πfct−Asg(t)sin2πfct,0≤t≤Ts
其等效基带信号为
[
A
c
+
j
A
s
]
g
(
t
)
[A_c+jA_s]g(t)
[Ac+jAs]g(t)。
2、MQAM 信号的矢量表示
取正交函数:
f
1
(
t
)
=
2
ε
g
g
(
t
)
c
o
s
ω
c
t
f_1(t)=\sqrt{\frac{2}{\varepsilon_g}}g(t)cos\omega_ct
f1(t)=εg2g(t)cosωct,
f
2
(
t
)
=
2
ε
g
g
(
t
)
s
i
n
ω
c
t
f_2(t)=\sqrt{\frac{2}{\varepsilon_g}}g(t)sin\omega_ct
f2(t)=εg2g(t)sinωct
则:
s
m
(
t
)
=
A
c
ε
g
2
f
1
(
t
)
+
A
s
ε
g
2
f
2
(
t
)
s_m(t)=A_c\sqrt{\frac{\varepsilon_g}{2}}f_1(t)+A_s\sqrt{\frac{\varepsilon_g}{2}}f_2(t)
sm(t)=Ac2εgf1(t)+As2εgf2(t)
因此,
s
m
(
t
)
s_m(t)
sm(t) 可以用二维空间中的星座点
(
A
c
ε
g
2
,
A
s
ε
g
2
)
(A_c\sqrt{\frac{\varepsilon_g}{2}},A_s\sqrt{\frac{\varepsilon_g}{2}})
(Ac2εg,As2εg) 表示,若
A
c
=
(
2
n
−
1
−
M
)
d
,
A
s
=
(
2
k
−
1
−
M
)
d
A_c=(2n-1-\sqrt{M})d,A_s=(2k-1-\sqrt{M})d
Ac=(2n−1−M)d,As=(2k−1−M)d,
k
,
n
=
1
,
2
,
.
.
.
M
k,n=1,2,...\sqrt{M}
k,n=1,2,...M
当 M=16,
A
c
=
±
d
,
±
3
d
,
A
s
=
±
d
,
±
3
d
A_c=\pm d,\pm 3d,A_s=\pm d,\pm 3d
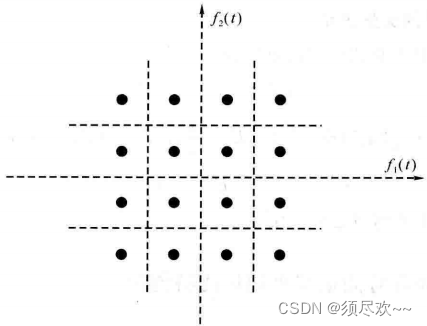
Ac=±d,±3d,As=±d,±3d,得到典型的 16QAM 星座图如下图所示:
四、正交 MFSK(M维信号)
1、正交 MFSK 简介
用不同频率的余弦载波波形一一对应 M 进制符号,则得到 MFSK 信号,其信号可写成:
s
m
(
t
)
=
A
c
o
s
(
2
π
f
c
t
+
2
π
m
Δ
f
t
)
,
m
=
1
,
2
,
.
.
.
,
M
s_m(t)=Acos(2\pi f_ct+2\pi m\Delta ft),m=1,2,...,M
sm(t)=Acos(2πfct+2πmΔft),m=1,2,...,M
其等效基带信号为
s
m
(
t
)
~
=
A
e
j
2
π
m
Δ
f
t
\tilde{s_m(t)}=Ae^{j2\pi m\Delta ft}
sm(t)~=Aej2πmΔft,为了保证这 M 个信号互相正交,要求最小的
Δ
f
=
1
2
T
s
\Delta f=\frac{1}{2T_s}
Δf=2Ts1
2、M 进制正交信号的矢量表示
M 进制正交信号可以表示为:
s
m
(
t
)
=
E
s
f
m
(
t
)
s_m(t)=\sqrt{E_s}f_m(t)
sm(t)=Esfm(t)
这里,
f
m
(
t
)
=
2
T
s
c
o
s
(
2
π
f
c
t
+
π
m
t
T
s
)
f_m(t)=\sqrt{\frac{2}{T_s}}cos(2\pi f_ct+\frac{\pi mt}{T_s})
fm(t)=Ts2cos(2πfct+Tsπmt),
E
s
=
1
2
A
2
T
s
E_s=\frac{1}{2}A^2T_s
Es=21A2Ts,所以,
s
m
(
t
)
s_m(t)
sm(t) 可以用点(
E
s
,
0
,
0
,
.
.
.
,
0
\sqrt{E_s},0,0,...,0
Es,0,0,...,0)、(
0
,
E
s
,
0
,
.
.
.
,
0
0,\sqrt{E_s},0,...,0
0,Es,0,...,0)、(
0
,
0
,
E
s
,
.
.
.
,
0
0,0,\sqrt{E_s},...,0
0,0,Es,...,0)…(
0
,
0
,
0
,
.
.
.
,
E
s
0,0,0,...,\sqrt{E_s}
0,0,0,...,Es)
表示,两点之间的最小距离 d m i n = 2 E s d_{min}=\sqrt{2E_s} dmin=2Es
五、MATLAB 仿真
场景:设信道加性高斯白噪声的双边功率谱密度为 N 0 / 2 N_0/2 N0/2,发送信号平均每符号能量 E s E_s Es,利用 MATLAB ,通过仿真的方法仿真 QPSK 系统在 AWGN 信道下的性能
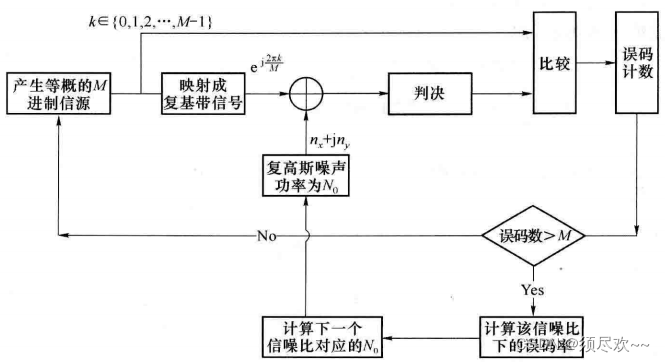
思路:利用 MATLAB ,可以通过蒙特卡罗仿真的方式得到 MPSK 系统的误码率,如下图所示
1、MATLAB 源码
%MPSK系统系统的仿真
clear all;
close all;
M=4; %QPSK
EsN0dB = 3:0.5:10;
EsN0 = 10.^( EsN0dB/10 );
Es = 1;
N0 = 10.^( -EsN0dB/10 );
sigma = sqrt(N0/2);
error = zeros(1,length(EsN0dB));
s_data = zeros(1,length(EsN0dB));
for k=1:length(EsN0dB)
error(k)=0;
s_data(k) = 0;
while error(k)<1000
%产生信源 1,2,3,4均匀分布
d = ceil( rand(1,10000)*M );
%调制成QPSK信号(复基带形式)
s = sqrt(Es)*exp(j*2*pi/M*(d-1));
%加入信道噪声(复噪声)
r = s + sigma(k)*( randn(1,length(d)) + j*randn(1,length(d)) );
%判决
for m=1:M %计算距离
rd(m,:) = abs( r - sqrt(Es)*exp(j*2*pi/M*(m-1)) );
end
for m=1:length(s) %判决距离最近的点
dd(m) = find( rd(:,m) == min(rd(:,m)) );
if dd(m)~=d(m)
error(k) = error(k)+1;
end
end
s_data(k) = s_data(k)+10000;
end
% drawnow
% semilogy(EsN0dB, error./(s_data+eps)); hold on;
end
Pe = error./s_data;
%理论计算的误码率结果
Ps = erfc( sqrt(EsN0)*sin(pi/M) );
semilogy(EsN0dB,Pe,'b*-'); hold on;
semilogy(EsN0dB,Ps,'rd-');
xlabel('Es/N0(dB)'); ylabel('误码率');
legend('仿真结果','理论计算结果');
2、仿真及结果
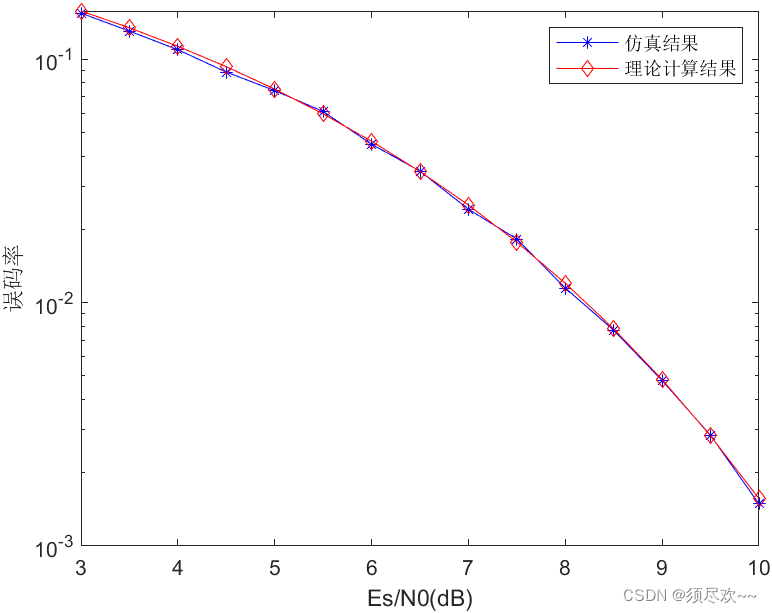
从上图可以看到,仿真结果与理论计算结果的误码率曲线基本重合。
我的qq:2442391036,欢迎交流!