局部用各种方法
按知识点汇总其各自记忆方法
整式:六大公式
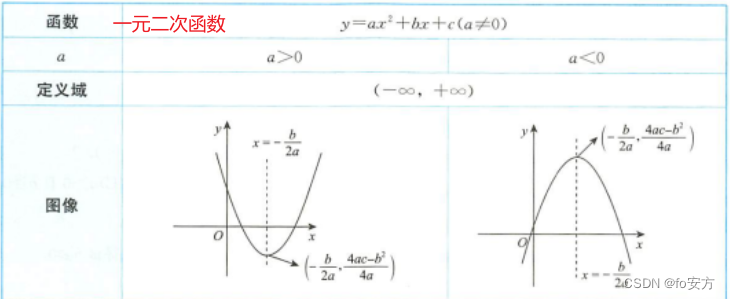
函数:一元二次函数【图像(形状,上下,交点)
⟹
\Longrightarrow
⟹
△
△
△
⟹
\Longrightarrow
⟹ 抛物线与x轴交点
⟹
\Longrightarrow
⟹ 交点图形】
方程:一元二次方程【根(多少,正负,区间)
⟹
\Longrightarrow
⟹
△
△
△
⟹
\Longrightarrow
⟹ 求根公式
x
1
,
2
x_{1,2}
x1,2=
−
b
±
△
2
a
\frac{-b±\sqrt{△}}{2a}
2a−b±△
⟹
\Longrightarrow
⟹ 韦达定理
⟹
\Longrightarrow
⟹ 判断两根符号情况,即根多少由
△
△
△判断,根需要求根公式,求根公式可推导韦达定理,韦达定理可判断两根符号情况。】
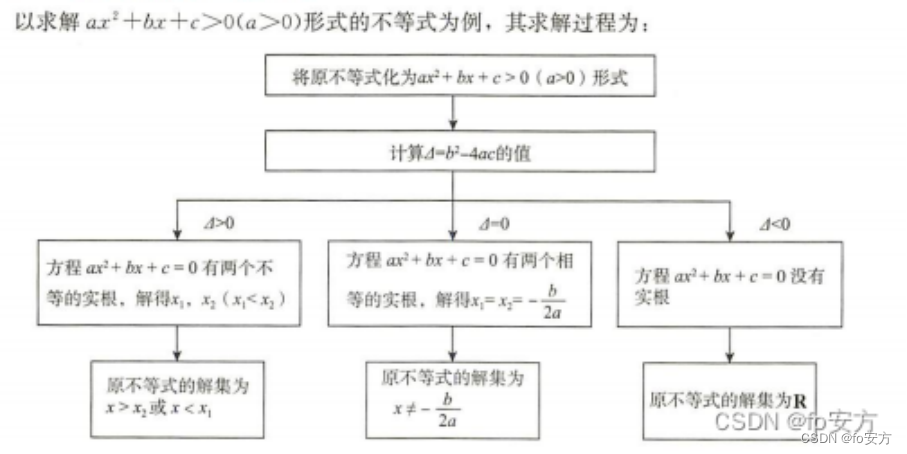
不等式:一元二次不等式【11】、均值不等式【完全平方→均值不等式→求最值→前提为“一正二定三相等”→“正”为正数,“定”为定值,“相等”为等号成立】、
PS:
学习记忆——数学篇——汇总——顺口溜记忆法+谐音记忆法+理解记忆法+归类记忆法+重点记忆法+比较记忆法+转图像记忆法
数字编码法
学习记忆——记忆宫殿——编码——数字编码和字母编码——两位数
学习记忆——记忆宫殿——编码——数字编码——数字声母
学习记忆——英语——字母编码
1.一元二次方程
a
x
2
+
b
x
+
c
=
0
ax^2+bx+c=0
ax2+bx+c=0:
根判别式:
△
=
b
2
−
4
a
c
△=b^2-4ac
△=b2−4ac:跟盘别试,比尔见识苹果月亮
根:
x
=
−
b
2
a
x=-\frac{b}{2a}
x=−2ab:阿克斯,伏笔除二苹果。伏笔初二苹果。阿克斯伏笔出一二苹果。阿克思福必出一二苹果。
2.二次函数
y
=
a
x
2
+
b
x
+
c
y=ax^2+bx+c
y=ax2+bx+c:
最值:
y
=
4
a
c
−
b
2
4
a
y=\frac{4ac-b^2}{4a}
y=4a4ac−b2:外,死苹果月亮见比尔厨艺死苹果。死苹果见比尔出一丝苹果 。
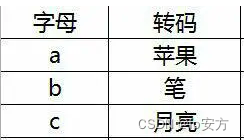

根判别式=笔方-4个苹果月亮=笔儿见死苹果月亮
比尔见识苹果月亮
归类记忆法
一元二次函数的形式:标准式、配方式、零点式
一元二次函数的公式:一般式,顶点式,两根式,求根公式,判别式,对称轴,顶点坐标,最值
一元二次函数公式总结
一般式:
y
=
a
x
2
+
b
x
+
c
(
a
≠
0
)
y=ax^2+bx+c(a≠0)
y=ax2+bx+c(a=0)
顶点式:
y
=
a
(
x
+
b
2
a
)
2
+
4
a
c
−
b
2
4
a
y=a(x+\frac{b}{2a})^2+\frac{4ac-b^2}{4a}
y=a(x+2ab)2+4a4ac−b2,顶点坐标为
(
−
b
2
a
,
4
a
c
−
b
2
4
a
)
(-\frac{b}{2a},\frac{4ac-b^2}{4a})
(−2ab,4a4ac−b2)
两根式:
y
=
a
(
x
−
x
1
)
(
x
−
x
2
)
y=a(x-x_1)(x-x_2)
y=a(x−x1)(x−x2),
x
1
,
x
2
x_1,x_2
x1,x2是函数的两个根
求根公式:
x
12
=
−
b
±
b
2
−
4
a
c
2
a
x_{12}=\frac{-b±\sqrt{b^2-4ac}}{2a}
x12=2a−b±b2−4ac
判别式:
△
=
b
2
−
4
a
c
△=b^2-4ac
△=b2−4ac
韦达定理:
x
1
+
x
2
=
−
b
a
x_1+x_2=-\frac{b}{a}
x1+x2=−ab,
x
1
⋅
x
2
=
c
a
x_1·x_2=\frac{c}{a}
x1⋅x2=ac【注意用韦达定理之前验证判别式大于等于零】
图形结合法
函数最重要的就是图
函数最重要的就是图,记忆图像,可以辅助记忆住很多性质
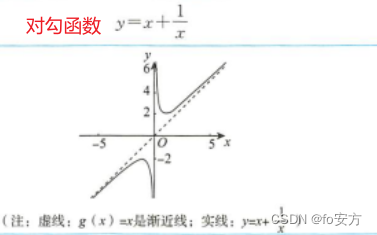
重点记忆法
抓住一个重点,去推导,去联想。
△ △ △判别式 ⟹ \Longrightarrow ⟹ b 2 − 4 a c b^2-4ac b2−4ac ⟹ \Longrightarrow ⟹ △ △ △>0, x x x= − b ± △ 2 a \frac{-b±\sqrt{△}}{2a} 2a−b±△ → △ △ △=0, x x x为 − b 2 a -\frac{b}{2a} −2ab ⟹ \Longrightarrow ⟹ y y y的最值 4 a c − b 2 4 a \frac{4ac-b^2}{4a} 4a4ac−b2 = -△ 4 a \frac{-△}{4a} 4a-△
完全平方
(
a
+
b
)
2
≥
0
(a+b)^2≥0
(a+b)2≥0
⟹
\Longrightarrow
⟹
a
+
b
2
≥
a
b
\frac{a+b}{2}≥\sqrt{ab}
2a+b≥ab
⟹
\Longrightarrow
⟹均值不等式
x
1
+
x
2
+
x
3
+
.
.
.
+
x
n
n
≥
x
1
⋅
x
2
⋅
x
3
⋅
.
.
.
⋅
x
n
n
\frac{x_1+x_2+x_3+...+x_n}{n}≥\sqrt[n]{x_1·x_2·x_3·...·x_n}
nx1+x2+x3+...+xn≥nx1⋅x2⋅x3⋅...⋅xn
⟹
\Longrightarrow
⟹求最值
⟹
\Longrightarrow
⟹前提为“一正二定三相等”
⟹
\Longrightarrow
⟹“正”为各项为正数,“定”为积/和为定值,“相等”为等号成立需各项相等
算术平均值大于几何平均值→均值不等式
等差中项公式→等差数列奇数项和与偶数项和之差与之比
歌决记忆法/顺口溜记忆法
糖水不等式:糖水加糖,越加越甜
不等式组的解集:大大取大,小小取小;大小、小大中间找;大大、小小解不了
均值不等式:和有定值积最大,积有定值和最小
穿线法原则:奇穿偶不穿
复合函数单调性:同增异减
倒数根问题:b变号,根变号;ac互换,根为倒
等差数列
a
n
a_n
an的系数特征:一次项系数是公差,系数之和是首项
等差数列
S
n
S_n
Sn的系数特征:二次项系数是半公差,系数之和是首项
等比数列正负性:同奇同偶项,正负性一样
不等式:大于取两边,小于取中间

大鱼(于)吃(取)两边,
小鱼(于)吃(取)中间。
场景:小鱼是大鱼的儿子,大鱼们保护小鱼,所以让小鱼在中间吃。
糖水不等式:糖水加糖,越加越甜
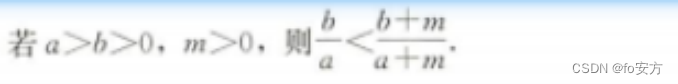
均值不等式:和定积最大,积定和最小,一正二定三相等
鹤顶鸡最大
机顶盒最小
核顶极大
鸡丁核小
分式不等式:穿线法:奇穿偶不穿
等差数列 a n a_n an与 S n S_n Sn相互转换
S
n
=
d
2
n
2
+
(
a
1
−
d
2
)
n
=
C
n
2
+
D
n
S_n=\frac{d}{2}n^2+(a_1-\frac{d}{2})n=Cn^2+Dn
Sn=2dn2+(a1−2d)n=Cn2+Dn,于是
d
=
2
C
d=2C
d=2C,
a
1
=
C
+
D
a_1=C+D
a1=C+D。
d为最高次项系数和次数的乘积,
a
1
a_1
a1为各项系数之和。
等比数列:正负性:同奇同偶项,正负性一样
谐音记忆法
连续等长片段和,等差的新公差为项数平方乘旧公差,等比的新公比为旧公比的项数次方。
项数平方乘旧公差=香树平芳呈旧贡茶
旧公比的项数次方=旧宫壁的橡树此房
理解记忆法
比较记忆法
转图像记忆法
结合字母编码
学习记忆——英语——字母编码
-
求根公式
x 1 , 2 x_{1,2} x1,2= − b ± △ 2 a \frac{-b±\sqrt{△}}{2a} 2a−b±△,很重要,可以推导出韦达定理等,故事如下:两个苹果(a)上面有个士兵(±),左手拿着香蕉(b)挡住箭(-),右边是一座桥,桥底有一个三角形。

-
一元二次方程的根: x = − b 2 a x=-\frac{b}{2a} x=−2ab:2座桥,桥上有一个香蕉,桥底有两个苹果。
或者:两颗苹果上面有根香蕉,要想托稳香蕉,得有两个横版(一个负号,一个除号)。

或者两个苹果上面有一座桥和一根香蕉

3.
y
=
a
x
2
+
b
x
+
c
y=ax^2+bx+c
y=ax2+bx+c的最值:
4
a
c
−
b
2
4
a
\frac{4ac-b^2}{4a}
4a4ac−b2 =—
△
4
a
\frac{△}{4a}
4a△
4颗苹果上面有两座桥,桥上有一个三角形。


- 韦达定理
x为剪刀,a苹果,b香蕉,c月亮
剪头➕剪刀可以换,苹果顶着负香蕉
剪刀,剪刀,剪刀,可以换,苹果顶着月亮