作为资深的开发专家，我很高兴与您分享有关Java混淆的实际方案和案例。Java混淆是一种重要的安全措施，用于保护您的代码免受恶意分析和反编译的威胁。在本文中，我将介绍Java混淆的基本原理、常用工具，以及一个简单的案例来演示如何应用混淆来保护您的代码。

**Java混淆的基本原理**

Java混淆是一种通过修改Java源代码或字节码的方式，使其变得更难以理解和分析的技术。这可以通过重命名类、方法和变量，添加虚假代码，以及其他各种技术来实现。混淆后的代码在逻辑上与原始代码等效，但对于潜在的攻击者来说更加难以理解和破解。

**常用的Java混淆工具**

有许多Java混淆工具可供选择，每个都有其独特的特性和优点。以下是一些常见的Java混淆工具：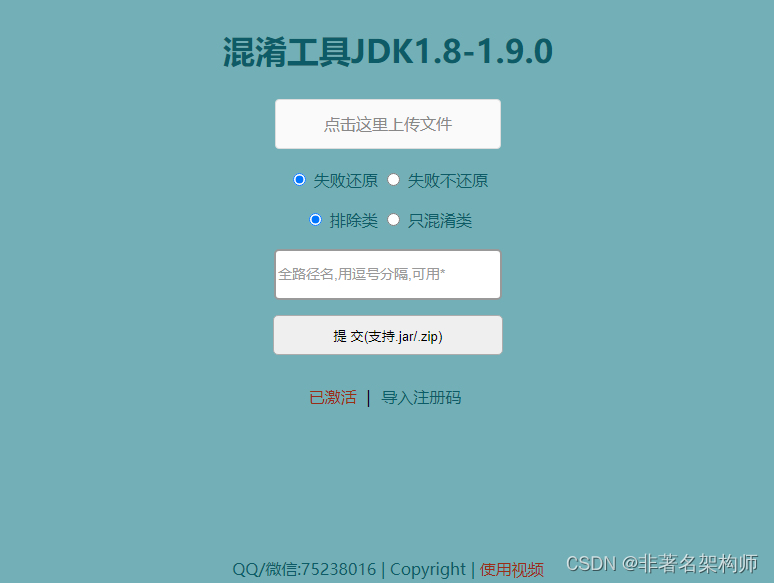



**Java混淆的实际案例**

让我们来看一个简单的Java混淆案例，假设我们有以下的Java类：

 

public class SampleClass {
    private String secretKey = "mySecretKey";
    
    public String getSecretKey() {
        return secretKey;
    }
}

攻击者可以轻松地反编译该类并获取`secretKey`的值。现在，让我们使用ProGuard来混淆这个类：

public class a {
    private String b = "mySecretKey";
    
    public String c() {
        return b;
    }
}

通过混淆，我们成功地将类名、字段名和方法名都进行了重命名，使得攻击者更难以理解代码的含义。

总结一下，Java混淆是一项关键的安全措施，可以帮助保护您的代码免受恶意分析和反编译的威胁。在实际应用中，您可以选择合适的混淆工具，并根据您的项目需求来配置混淆规则，以提高代码的安全性。希望这篇文章对您有所帮助！