题目
62. 不同路径
中等
相关标签
数学 动态规划 组合数学
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
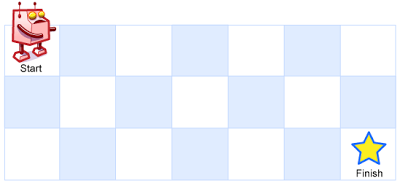
输入:m = 3, n = 7 输出:28
示例 2:
输入:m = 3, n = 2 输出:3 解释: 从左上角开始,总共有 3 条路径可以到达右下角。 1. 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 3. 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3 输出:28
示例 4:
输入:m = 3, n = 3 输出:6
提示:
1 <= m, n <= 100- 题目数据保证答案小于等于
2 * 109
思路和解题方法
- 首先,创建一个大小为m×n的二维数组
dp,并将所有元素初始化为0。这个二维数组用于保存到达每个位置的唯一路径数量。- 然后,通过两个循环分别将第一行和第一列的元素设置为1。因为从起点出发,只有一条路径可以到达第一行和第一列的任意位置。
- 接下来,使用两个嵌套的循环遍历除第一行和第一列之外的其他位置。对于每个位置
(i, j),它可以从上方的位置(i-1, j)或左边的位置(i, j-1)到达。因此,到达当前位置的唯一路径数量等于到达上方位置和左边位置的唯一路径数量之和,即dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。- 最后,返回
dp[m - 1][n - 1],即到达右下角位置的唯一路径数量。
复杂度
时间复杂度:
O(m*n)
时间复杂度为O(m*n),其中m和n分别是网格的行数和列数。这是因为代码中使用了两个嵌套的循环来遍历整个网格,所以时间复杂度与网格的大小成正比。
空间复杂度
O(n)
空间复杂度为O(n),其中n是网格的列数。这是因为代码使用了一个大小为n的一维数组
dp来保存到达每个位置的路径数。在算法执行过程中,只需要不断更新这个数组中的元素,所以只占用了常数级别的额外空间。因此,空间复杂度与网格的大小无关。
c++ 代码
class Solution {
public:
int uniquePaths(int m, int n) {
// 创建一个大小为m×n的二维数组,用于保存到达每个位置的唯一路径数量
vector<vector<int>> dp(m, vector<int>(n, 0));
// 将第一行的所有元素设置为1,因为从起点出发只有一条路径可以到达第一行的任意位置
for (int i = 0; i < m; i++)
dp[i][0] = 1;
// 将第一列的所有元素设置为1,因为从起点出发只有一条路径可以到达第一列的任意位置
for (int j = 0; j < n; j++)
dp[0][j] = 1;
// 使用动态规划的思想计算除第一行和第一列之外的其他位置的唯一路径数量
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
// 到达当前位置的唯一路径数量等于到达上方位置和左边位置的唯一路径数量之和
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
// 返回到达右下角位置的唯一路径数量
return dp[m - 1][n - 1];
}
};
优化空间代码
class Solution {
public:
int uniquePaths(int m, int n) {
// 创建一个大小为n的一维数组dp,用于保存到达每个位置的路径数
vector<int> dp(n);
// 初始化dp数组,将第一行的路径数都设置为1
for (int i = 0; i < n; i++) {
dp[i] = 1;
}
// 使用动态规划的思想计算到达每个位置的路径数
for (int j = 1; j < m; j++) {
for (int i = 1; i < n; i++) {
// 当前位置的路径数等于上方位置的路径数加左侧位置的路径数
dp[i] += dp[i - 1];
}
}
// 返回到达右下角位置的路径数,即dp数组的最后一个元素
return dp[n - 1];
}
};
解释
- 首先,创建一个大小为n的一维数组
dp,用于保存到达每个位置的路径数。- 然后,初始化
dp数组,将第一行的路径数都设置为1,因为在第一行的任意位置,只能向右移动,所以只有一条路径可选。- 接着,使用动态规划的思想计算到达每个位置的路径数。从第二行开始遍历到第m行,在每一行中,从第二列开始遍历到第n列,在每次循环中,当前位置的路径数等于上方位置的路径数加左侧位置的路径数,即
dp[i] += dp[i - 1]。- 最后,返回到达右下角位置的路径数,即
dp数组的最后一个元素。- 时间复杂度:O(m × n)
- 空间复杂度:O(n)
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。