一、本周周赛总结

• T1暴力。
• T2滑窗。
• T3二分。
• T4背包。

二、 [Easy] 6269. 到目标字符串的最短距离

链接: 6269. 到目标字符串的最短距离

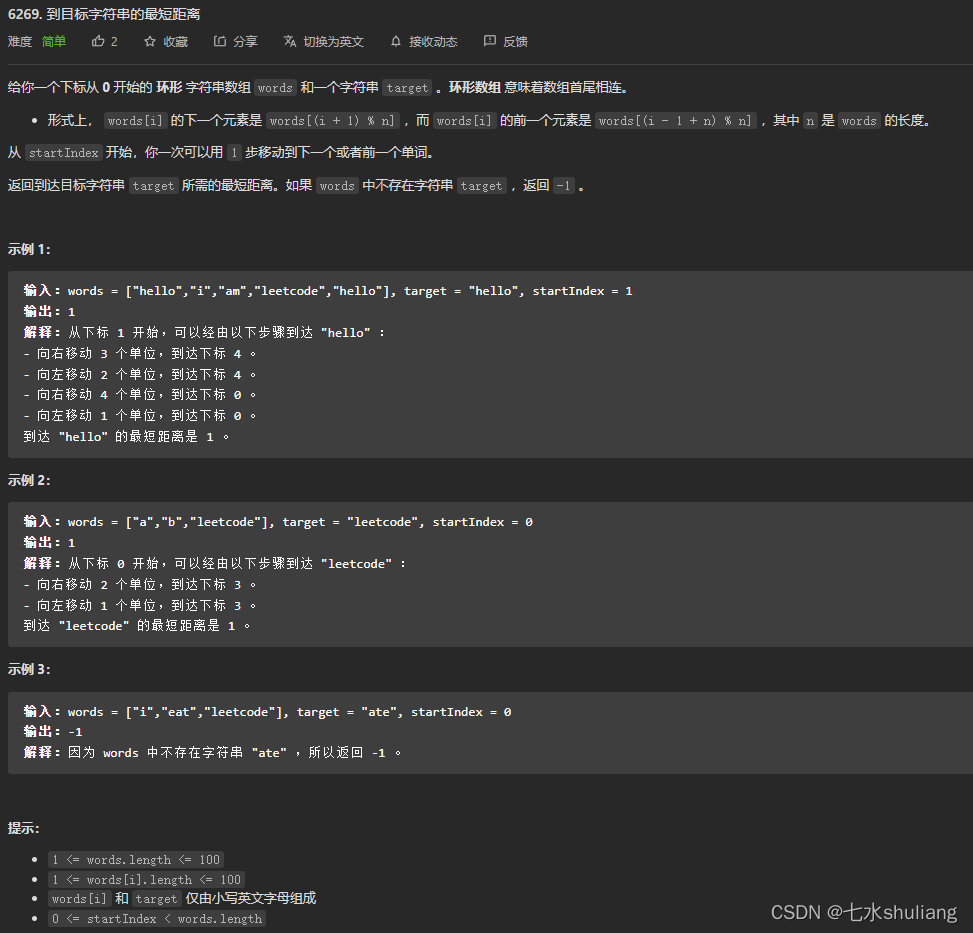
1. 题目描述

2. 思路分析

两种遍历，找最短的写。

3. 代码实现

class Solution:
    def closetTarget(self, words: List[str], target: str, startIndex: int) -> int:
        n = len(words)
        if target not in words:
            return -1
        # a = 0
        # for i in range(n):
        #     if words[(i+startIndex)%n] == target:
        #         a = i
        #         break
        # b = 0
        # for i in range(n):
        #     if words[(startIndex-i)%n] == target:
        #         b = i
        #         break
        # return min(a,b)
        ans = n
        for i,w in enumerate(words):
            if w == target:
                ans = min(ans,(i-startIndex)%n,(startIndex-i)%n)
        return ans

三、[Medium] 6270. 每种字符至少取 K 个

链接: 6270. 每种字符至少取 K 个

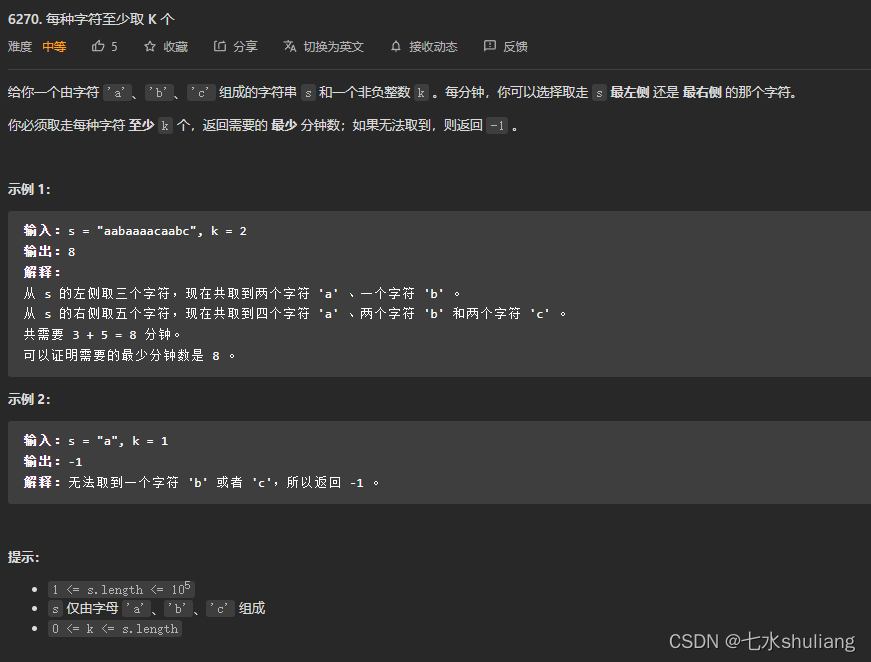
1. 题目描述

2. 思路分析

• 把s翻倍，然后在中间位置滑窗，即有效的答案窗口必须包含n-1或者n的位置。

---

• 灵神的思路是，先从后缀找到最小合法串，然后尝试增加前缀，减小后缀。

---

• 还有一种滑窗思路，从中间去掉最长一段，使剩下的abc个数满足题意；即中间段的abc个数需要<=原数-k

3. 代码实现

翻倍滑窗

class Solution:
    def takeCharacters(self, s: str, k: int) -> int:
        c = Counter(s)
        if any(c[x]<k for x in 'abc'):
            return -1
        if k == 0:
            return 0
        ss = s + s
        n = len(s)
        c = Counter()
        q = deque()
        ans = inf
        for r,v in enumerate(ss):
            c[v] += 1
            q.append(r)
            while q and c[ss[q[0]]] > k:
                c[ss[q.popleft()]] -= 1
            # print(c,q)
            if len(q)<ans and len(q)>=3*k and q[0]<=n and q[-1]>=n-1 and  c['a']>=k and c['b']>=k and c['c']>=k:
                  ans = len(q)
        return ans)

前后双指针

class Solution:
    def takeCharacters(self, s: str, k: int) -> int:
        c = Counter(s)
        if any(c[x]<k for x in 'abc'):
            return -1
        if k == 0:
            return 0
        j = n = len(s)
        c = Counter()        
        q = deque()
        while c['a']<k or c['b']<k or c['c']<k:            
            j -= 1
            q.appendleft(j)
            c[s[j]] += 1

        ans = len(q)
        for i,v in enumerate(s):
            c[v] += 1
            while q and c[s[q[0]]] > k:
                c[s[q.popleft()]] -= 1
            # print(c,q)
            ans = min(ans,len(q)+i+1)
        return ans

四、[Medium] 6271. 礼盒的最大甜蜜度

链接: 6271. 礼盒的最大甜蜜度

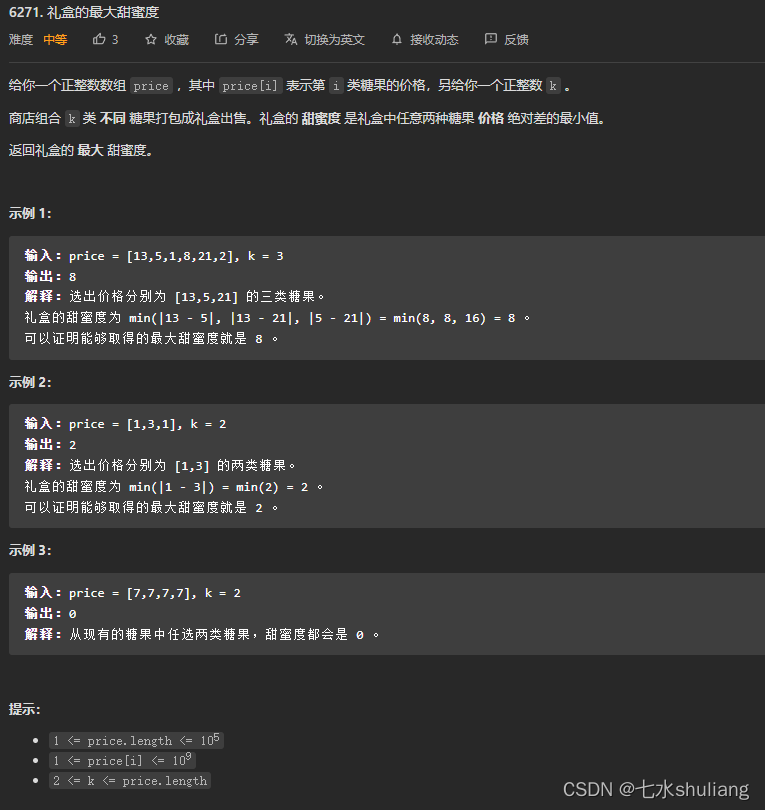
1. 题目描述

2. 思路分析

• 最小值最大化，又是二分。
• ok(x)代表任意差不小于x时，能否找出k类糖果；显然x越小，越能满足。单调的。
• ok函数内部贪心，由于要尽可能多去多选，因此可以必选最小的，然后向后尽可能取最近的满足超过x的糖果。计数能否满足k个即可。

3. 代码实现

class Solution:
    def maximumTastiness(self, price: List[int], k: int) -> int:
        n = len(price)
        mx = max(price) - min(price)
        if k == 2:
            return mx
        price.sort()
        
        def ok(x):
            # 二分判断模板，越小的x满足要求，则yes=0 no=1，答案应是最后一个0的位置即bisect_left(range(xxx),1,key=ok)-1
            yes,no = 0,1
            c = 1  # 计数
            pre = price[0]
            for p in price[1:]:
                if p-pre>=x:
                    c += 1
                    pre = p
                    if c>=k:
                        return yes  # 足够了
            return no
        
        return bisect_left(range(mx+1),1,key=ok)-1

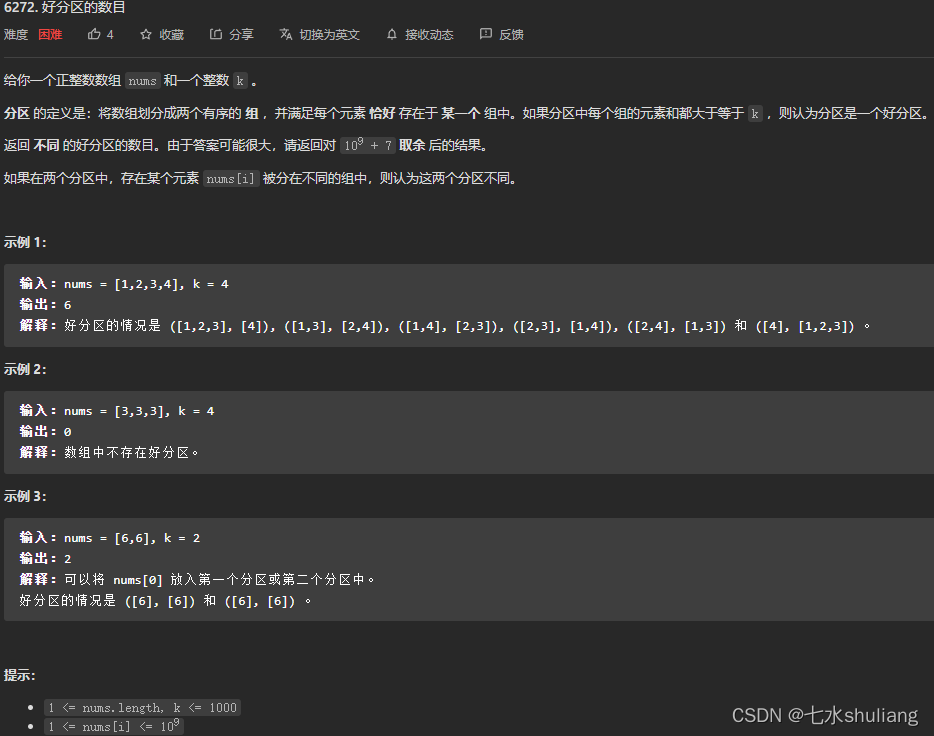
五、[Hard] 6272. 好分区的数目

链接: 6272. 好分区的数目

1. 题目描述

2. 思路分析

• 这题目一看像背包，但又发现要>=k的数量，不好写。
• 因此反着算，求<k的方案数，再计算总体方案数，相减即可。
• 比赛时由于不会特判错误情况，只能最后判断大小，导致中途不能取模，很可能TLE，但是赛后造了下数据没有TLE，很怪。可能力扣的数据量还是不够极限。
• 定义f[j]为取任意数求和为j的方案数，由于两边是对称的且不会重（提前特判了非法的重复），因此我们可以sum(f)*2来计算总的<k的方案数。

3. 代码实现

MOD = 10**9 + 7
class Solution:
    def countPartitions(self, nums: List[int], k: int) -> int:        
        # 特判很关键，代表任意分组都无法让两边同时满足；这样就会剔除背包计算出来的一边小于k,但另一边也小于k的重复数据
        # 即：背包的结果一定是一边小于k，而剩下的不小于k,对称无重复，可以放心乘2
        if k*2>sum(nums):  
            return 0
        f = [0]*k
        f[0] = 1
        for x in nums:
            for j in range(k-1,x-1,-1):
                f[j] = (f[j] + f[j-x]) % MOD
        return (pow(2, len(nums), MOD) - sum(f)*2%MOD) %MOD
        
        # # # #以下是错误答案，由于不会上边那个特判，因此只能最后判断大小，导致中途不敢取模，大数据必TLE
        # n = len(nums)
        # f = [0]*k
        # f[0] = 1
        # for x in nums:
        #     for j in range(k-1,x-1,-1):
        #         f[j] += f[j-x]
        # print(n)
        # a = 2**n
        # b = sum(f)*2
        # if a <= b:
        #     return 0
        # return (2**n - sum(f)*2)%MOD

六、参考链接