---

前言

1、组合总和
2、组合总和||

---

一、组合总和（力扣39）

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

思路：

关键在于 值可以重复使用，所以在进行递归传参数的时候不再是之前的 i+1 而是 i

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> paths = new LinkedList<>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        backtracking(candidates,target,0,0);
        return res;
    }
    public void backtracking(int[] candidates,int target,int sum,int startIndex){
        if(sum>target){
            return ;
        }
        if(sum==target){
            res.add(new ArrayList<>(paths));
            return ;
        }

        for(int i=startIndex;i<candidates.length;i++){
            paths.add(candidates[i]);
            sum += candidates[i];
            backtracking(candidates,target,sum,i);
            sum -= candidates[i];
            paths.removeLast();
        }
    }
}

剪枝优化

在for循环里做文章

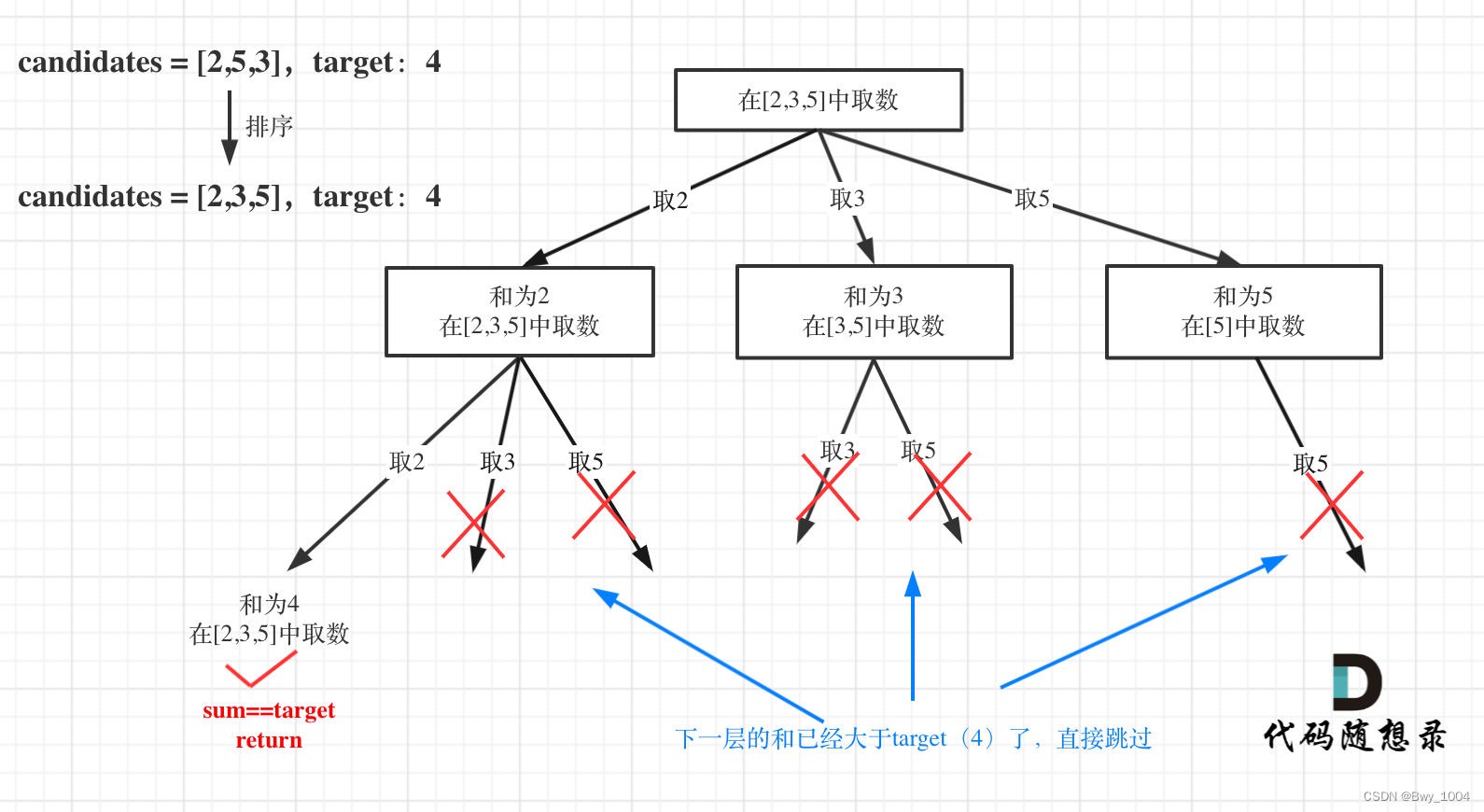
for循环剪枝代码如下：

for (int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++)

二、组合总和II（力扣40）

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

注意：解集不能包含重复的组合。

难点：
在于去重的问题

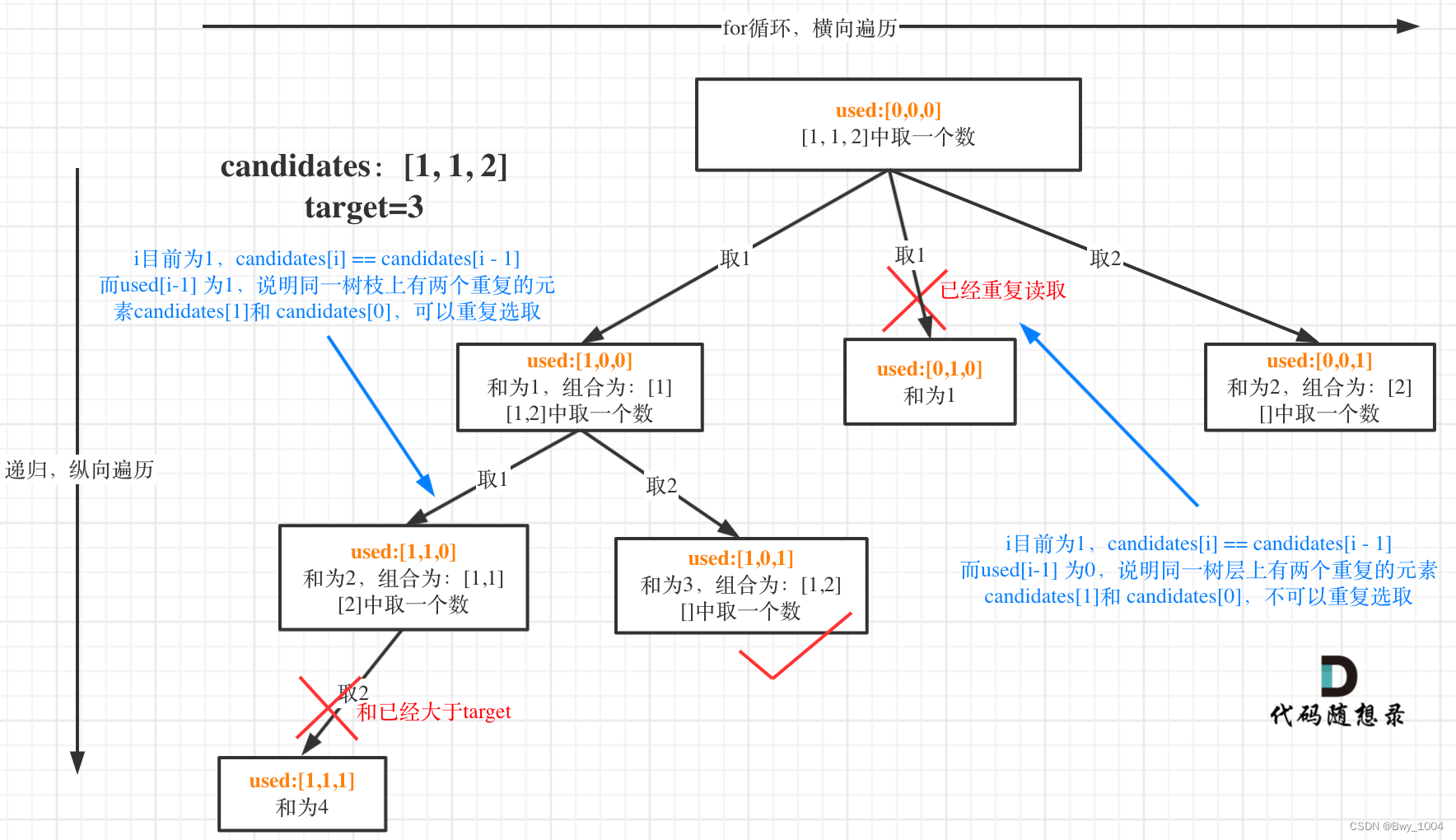
去重的逻辑 爵爵子，建议反复阅读！！！

链接: link

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> paths = new LinkedList<>();
    boolean[] used;

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        used = new boolean[candidates.length];
        Arrays.fill(used,false);
        //排序
        Arrays.sort(candidates);
        backtracking(candidates,target,0,0);
        return res;
    }
    public void backtracking(int[] candidates,int target,int sum,int startIndex){
        if(sum>target) return ;
        if(sum==target){
            res.add(new ArrayList<>(paths));
            return ;
        }
        for(int i=startIndex;i<candidates.length;i++){
            if(sum>target) break;
            if(i>0&&candidates[i]==candidates[i-1]&& used[i-1]==false) continue;//不处理
            paths.add(candidates[i]);
            used[i] = true;
            sum+=candidates[i];
            backtracking(candidates,target,sum,i+1);
            sum-=candidates[i];
            used[i]=false;
            paths.removeLast();
        }
    }
}

---