模式识别——高斯分类器
- 需知
- 定义
- 特殊情况(方差一致)
- Sigmoid
需知
所有问题定义在分类问题下,基于贝叶斯决策
定义
条件概率为多元高斯分布,此时观测为向量
X
=
X
1
,
X
2
,
.
.
.
,
X
n
X={X_1,X_2,...,X_n}
X=X1,X2,...,Xn,通过极大后验展开可以得到最优决策函数:

决策函数可以写为:

d
d
d就是马氏距离,代表两个高斯分布之间的距离。而
α
\alpha
α则代表了类别的先验。
特殊情况(方差一致)
方差一致的话分类器就是线性的。



Sigmoid
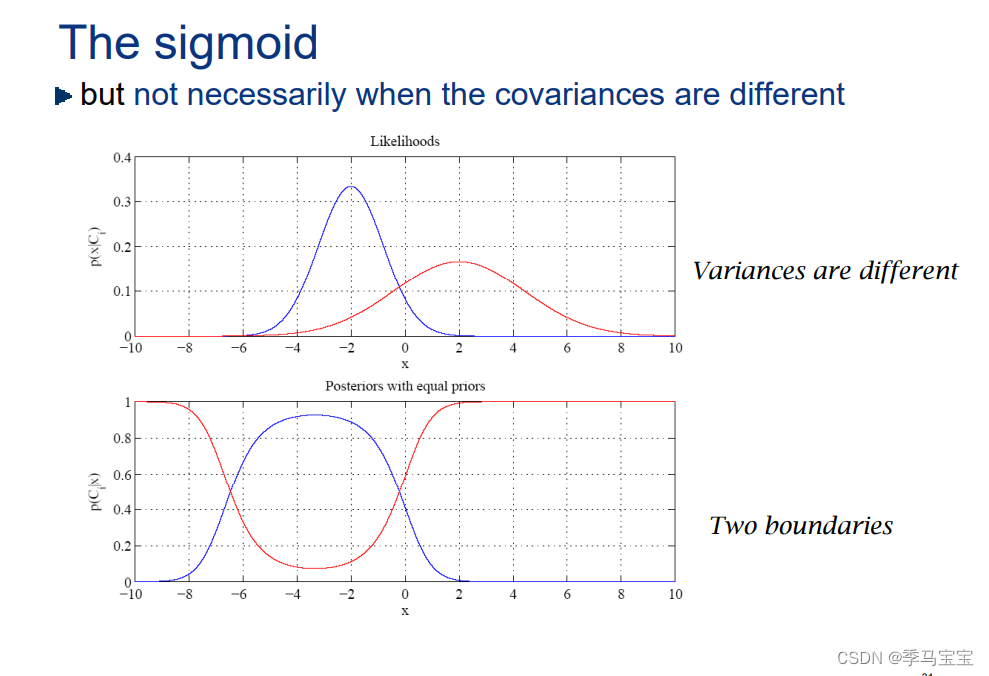
使用原始的BDR定义可以推导出,每个类别的概率概率为sigmoid函数(原始定义考虑观测的边缘概率,所以计算的就是概率(概率和为1),所以为sigmoid函数。而在决策时不考虑边缘概率,约掉了归一化参数,其实两者的判决边界仍然是相同的)


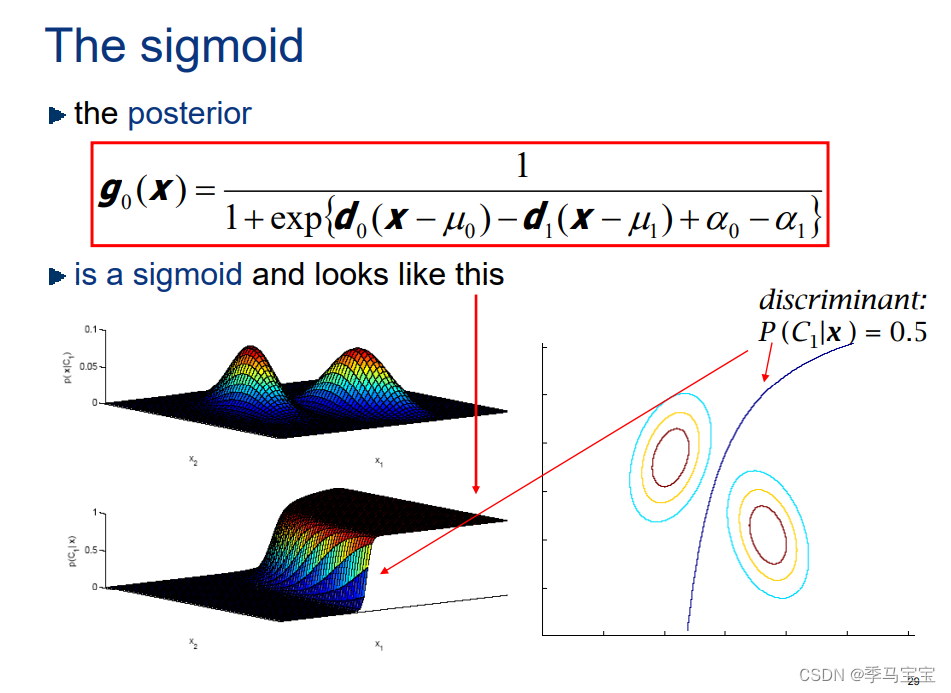
协方差一致有唯一分界线:

协方差不一致有两个分界线: