深度学习——批量规范化(Batch Normalization)
文章目录
- 前言
- 一、训练深层网络
- 二、批量规范化层
- 2.1. 全连接层
- 2.2. 卷积层
- 2.3. 预测过程中的批量规范化
- 三、从零实现
- 四、使用批量规范化层的LeNet
- 五、简洁实现
- 六、小结
- 总结
前言
训练深层神经网络是十分困难的,特别是在较短的时间内使他们收敛更加棘手。 本章将学习批量规范化(batch normalization),这是一种流行且有效的技术,可持续加速深层网络的收敛速度。
一、训练深层网络
批量规范化应用于单个可选层(也可以应用到所有层),
其原理如下:在每次训练迭代中,我们首先规范化输入,即通过减去其均值并除以其标准差,其中两者均基于当前小批量处理。接下来,我们应用比例系数和比例偏移。
正是由于这个基于批量统计的标准化,才有了批量规范化的名称。
请注意,在应用批量规范化时,批量大小的选择可能比没有批量规范化时更重要。
用x∈B表示一个来自小批量B的输入,批量规范化BN根据以下表达式转换x
B N ( x ) = γ ⊙ x − μ ^ B σ ^ B + β . \mathrm{BN}(\mathbf{x}) = \boldsymbol{\gamma} \odot \frac{\mathbf{x} - \hat{\boldsymbol{\mu}}_\mathcal{B}}{\hat{\boldsymbol{\sigma}}_\mathcal{B}} + \boldsymbol{\beta}. BN(x)=γ⊙σ^Bx−μ^B+β.
μ
^
B
\hat{\boldsymbol{\mu}}_\mathcal{B}
μ^B是小批量
B
\mathcal{B}
B的样本均值,
σ
^
B
\hat{\boldsymbol{\sigma}}_\mathcal{B}
σ^B是小批量
B
\mathcal{B}
B的样本标准差。
应用标准化后,生成的小批量的平均值为0和单位方差为1。
由于单位方差(与其他一些魔法数)是一个主观的选择,因此我们通常包含拉伸参数(scale)
γ
\boldsymbol{\gamma}
γ和偏移参数(shift)
β
\boldsymbol{\beta}
β,它们的形状与
x
\mathbf{x}
x相同。
请注意,
γ
\boldsymbol{\gamma}
γ和
β
\boldsymbol{\beta}
β是需要与其他模型参数一起学习的参数。
由于在训练过程中,中间层的变化幅度不能过于剧烈,而批量规范化将每一层主动居中,并将它们重新调整为给定的平均值和大小(通过 μ ^ B \hat{\boldsymbol{\mu}}_\mathcal{B} μ^B和 σ ^ B {\hat{\boldsymbol{\sigma}}_\mathcal{B}} σ^B)。
我们计算出的 μ ^ B \hat{\boldsymbol{\mu}}_\mathcal{B} μ^B和 σ ^ B {\hat{\boldsymbol{\sigma}}_\mathcal{B}} σ^B,如下所示:
μ ^ B = 1 ∣ B ∣ ∑ x ∈ B x , σ ^ B 2 = 1 ∣ B ∣ ∑ x ∈ B ( x − μ ^ B ) 2 + ϵ . \begin{aligned} \hat{\boldsymbol{\mu}}_\mathcal{B} &= \frac{1}{|\mathcal{B}|} \sum_{\mathbf{x} \in \mathcal{B}} \mathbf{x},\\ \hat{\boldsymbol{\sigma}}_\mathcal{B}^2 &= \frac{1}{|\mathcal{B}|} \sum_{\mathbf{x} \in \mathcal{B}} (\mathbf{x} - \hat{\boldsymbol{\mu}}_{\mathcal{B}})^2 + \epsilon.\end{aligned} μ^Bσ^B2=∣B∣1x∈B∑x,=∣B∣1x∈B∑(x−μ^B)2+ϵ.
在方差估计值中添加一个小的常量 ϵ > 0 \epsilon > 0 ϵ>0,以确保我们永远不会尝试除以零,即使在经验方差估计值可能消失的情况下也是如此。估计值 μ ^ B \hat{\boldsymbol{\mu}}_\mathcal{B} μ^B和 σ ^ B {\hat{\boldsymbol{\sigma}}_\mathcal{B}} σ^B通过使用平均值和方差的噪声估计来抵消缩放问题。
由于尚未在理论上明确的原因,优化中的各种噪声源通常会导致更快的训练和较少的过拟合:这种变化似乎是正则化的一种形式。
另外,批量规范化层在”训练模式“(通过小批量统计数据规范化)和“预测模式”(通过数据集统计规范化)中的功能不同。
- 在训练过程中,我们无法得知使用整个数据集来估计平均值和方差,所以只能根据每个小批次的平均值和方差不断训练模型。
- 而在预测模式下,可以根据整个数据集精确计算批量规范化所需的平均值和方差。
二、批量规范化层
批量规范化和其他层之间的一个关键区别是,由于批量规范化在完整的小批量上运行,因此我们不能像以前在引入其他层时那样忽略批量大小。
我们在下面讨论这两种情况:全连接层和卷积层,他们的批量规范化实现略有不同。
2.1. 全连接层
通常,我们将批量规范化层置于全连接层中的仿射变换和激活函数之间。
设全连接层的输入为x,权重参数和偏置参数分别为
W
\mathbf{W}
W和
b
\mathbf{b}
b,激活函数为
ϕ
\phi
ϕ,批量规范化的运算符为
B
N
\mathrm{BN}
BN。
那么,使用批量规范化的全连接层的输出的计算详情如下:
h = ϕ ( B N ( W x + b ) ) . \mathbf{h} = \phi(\mathrm{BN}(\mathbf{W}\mathbf{x} + \mathbf{b}) ). h=ϕ(BN(Wx+b)).
2.2. 卷积层
对于卷积层,我们可以在卷积层之后和非线性激活函数之前应用批量规范化。
当卷积有多个输出通道时,我们需要对这些通道的“每个”输出执行批量规范化,每个通道都有自己的拉伸和偏移参数,这两个参数都是标量。
假设我们的小批量包含
m
m
m个样本,并且对于每个通道,卷积的输出具有高度
p
p
p和宽度
q
q
q。
那么对于卷积层,我们在每个输出通道的
m
⋅
p
⋅
q
m \cdot p \cdot q
m⋅p⋅q个元素上同时执行每个批量规范化。
因此,在计算平均值和方差时,我们会收集所有空间位置的值,然后在给定通道内应用相同的均值和方差,以便在每个空间位置对值进行规范化。
2.3. 预测过程中的批量规范化
将训练好的模型用于预测时,我们不再需要样本均值中的噪声以及在微批次上估计每个小批次产生的样本方差了。
我们可能需要使用我们的模型对逐个样本进行预测。
一种常用的方法是通过移动平均估算整个训练数据集的样本均值和方差,并在预测时使用它们得到确定的输出。
可见,和暂退法一样,批量规范化层在训练模式和预测模式下的计算结果也是不一样的。
三、从零实现
我们从头开始实现一个具有张量的批量规范化层。
# 从零实现一个具有张量的批量规范化层
def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
# 通过is_grad_enabled方法来判断当前模式是训练模式还是预测模式
if not torch.is_grad_enabled():
# 如果是在预测模式下,直接使用传入的移动平均所得的均值和方差
X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
else:
assert len(X.shape) in (2, 4)
if len(X.shape) == 2:
# 使用全连接层的情况,计算特征维上的均值和方差
mean = X.mean(dim=0)
var = ((X - mean) ** 2).mean(dim=0)
else:
# 使用二维卷积层的情况,计算通道维上(axis=1)的均值和方差。
# 这里我们需要保持X的形状以便后面可以做广播运算
mean = X.mean(dim=(0, 2, 3), keepdim=True)
var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)
# 训练模式下,用当前的均值和方差做标准化
X_hat = (X - mean) / torch.sqrt(var + eps)
# 更新移动平均的均值和方差
moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
moving_var = momentum * moving_var + (1.0 - momentum) * var
Y = gamma * X_hat + beta # 缩放和移位
return Y, moving_mean.data, moving_var.data
我们现在可以创建一个正确的BatchNorm层。 这个层将保持适当的参数:拉伸gamma和偏移beta,这两个参数将在训练过程中更新。
此外,我们的层将保存均值和方差的移动平均值,以便在模型预测期间随后使用。
class BatchNorm(nn.Module):
def __init__(self, num_features, num_dims):
super().__init__()
if num_dims == 2:
shape = (1, num_features)
else:
shape = (1, num_features, 1, 1)
# 参与求梯度和迭代的拉伸和偏移参数,分别初始化成1和0
self.gamma = nn.Parameter(torch.ones(shape))
self.beta = nn.Parameter(torch.zeros(shape))
# 非模型参数的变量初始化为0和1
self.moving_mean = torch.zeros(shape)
self.moving_var = torch.ones(shape)
def forward(self, X):
# 如果X不在内存上,将moving_mean和moving_var复制到X所在显存上
if self.moving_mean.device != X.device:
self.moving_mean = self.moving_mean.to(X.device)
self.moving_var = self.moving_var.to(X.device)
# 保存更新过的moving_mean和moving_var
Y, self.moving_mean, self.moving_var = batch_norm(X, self.gamma, self.beta, self.moving_mean,
self.moving_var, eps=1e-5, momentum=0.9)
return Y
四、使用批量规范化层的LeNet
为了更好理解如何应用BatchNorm,下面我们将其应用于LeNet模型
net = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5), BatchNorm(6, num_dims=4), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), BatchNorm(16, num_dims=4), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),
nn.Linear(16 * 4 * 4, 120), BatchNorm(120, num_dims=2), nn.Sigmoid(),
nn.Linear(120, 84), BatchNorm(84, num_dims=2), nn.Sigmoid(),
nn.Linear(84, 10)
)
lr, num_epochs, batch_size = 1.0, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
d2l.plt.show()
# 来看看从第一个批量规范化层中学到的[拉伸参数gamma和偏移参数beta]。
print(net[1].gamma.reshape((-1,)), net[1].beta.reshape((-1,)))
print(len(net))
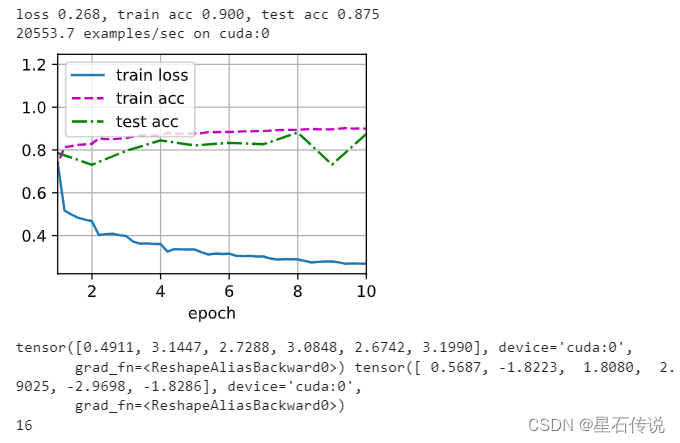
五、简洁实现
除了使用我们刚刚定义的BatchNorm,也可以直接使用深度学习框架中定义的BatchNorm。
net = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5), nn.BatchNorm2d(6), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), nn.BatchNorm2d(16), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),
nn.Linear(256, 120), nn.BatchNorm1d(120), nn.Sigmoid(),
nn.Linear(120, 84), nn.BatchNorm1d(84), nn.Sigmoid(),
nn.Linear(84, 10)
)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
d2l.plt.show()
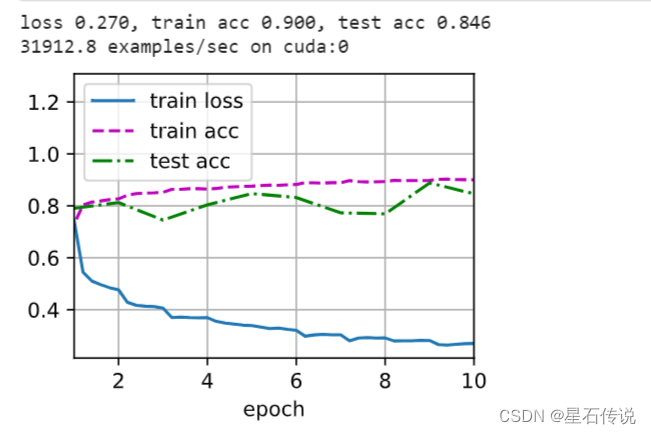
六、小结
- 在模型训练过程中,批量规范化利用小批量的均值和标准差,不断调整神经网络的中间输出,使整个神经网络各层的中间输出值更加稳定。
- 批量规范化在全连接层和卷积层的使用略有不同。(主要是因为卷积层具有通道维度,需要对每个通道的特征进行规范化)
- 批量规范化层和暂退层一样,在训练模式和预测模式下计算不同。
- 批量规范化有许多有益的副作用,主要是正则化,防止过拟合。
总结
**总之批量规范化通过对每个批次的输入进行均值和方差的归一化,**使得网络的输入分布更加稳定,有利于网络的收敛和训练的稳定性。(可以减轻网络对初始权重的依赖,使得神经网络更加鲁棒)。
欲穷千里目,更上一层楼。
–2023-10-15 进阶篇

![[机缘参悟-110] :一个IT人对面具的理解:职业面具戴久了,就会忘记原本真实的自己,一个人是忠于职位,还是忠于内心?](https://img-blog.csdnimg.cn/2464ef572c7c4e5c8eecf82a9cc13b89.png)