* @param {string} text1
* @param {string} text2
* @return {number}
*/
var longestCommonSubsequence = function(text1,text2) {
let dp =new Array(text2.length+1)
dp.fill(0)
for(let i = 1; i <= text1.length; i++) {
let pre = dp[0];
for(let j = 1; j <= text2.length; j++) {
let cur=dp[j]
if(text1[i-1] === text2[j-1]) {
dp[j] = pre + 1;
} else {
dp[j] = Math.max(dp[j], dp[j-1])
}
pre = cur;
}
}
return dp[text2.length];
};
思想
- dp[i][j]:长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]
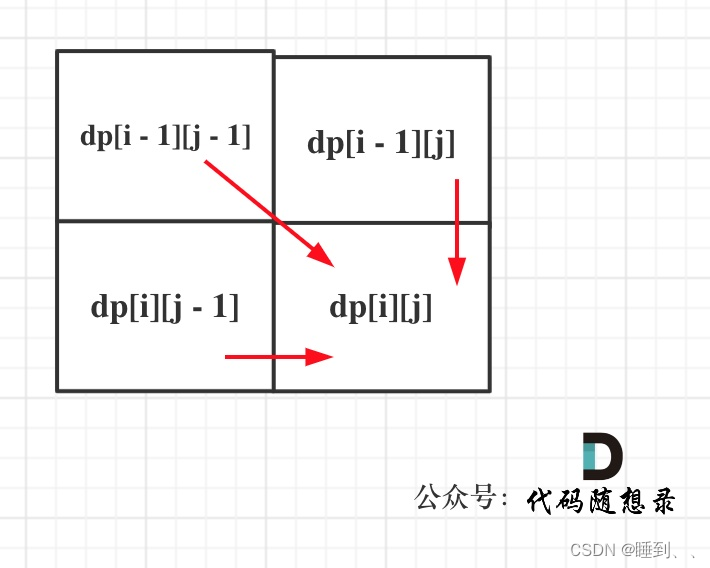
- 递推公式:
如果text1[i - 1] 与 text2[j - 1]相同,那么找到了一个公共元素,所以dp[i][j] = dp[i - 1][j - 1] + 1;
text1[i - 1] 与 text2[j - 1]不相同,dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]); - 确定遍历顺序
从前向后,从上到下来遍历这个矩阵。
 * 举例推导dp数组
* 举例推导dp数组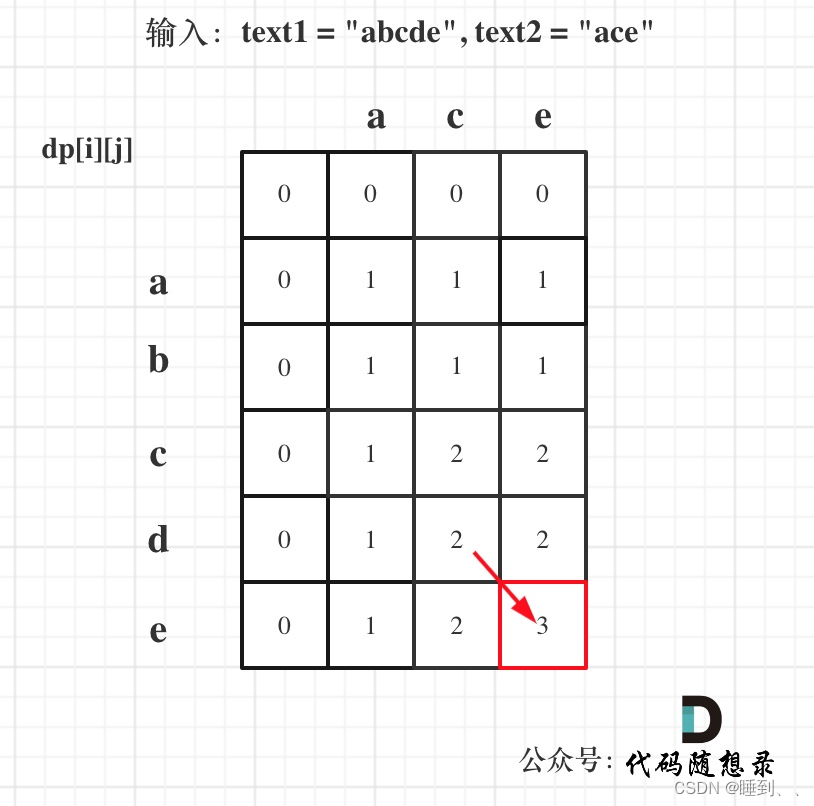
var maxSubArray = function(nums) {
const len = nums.length;
let dp = new Array(len).fill(0);
dp[0] = nums[0];
let max = dp[0];
for (let i = 1; i < len; i++) {
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
max = Math.max(max, dp[i]);
}
return max;
};
思想
- dp[i]:包括下标i(以nums[i]为结尾)的最大连续子序列和为dp[i]。
- 确定递推公式

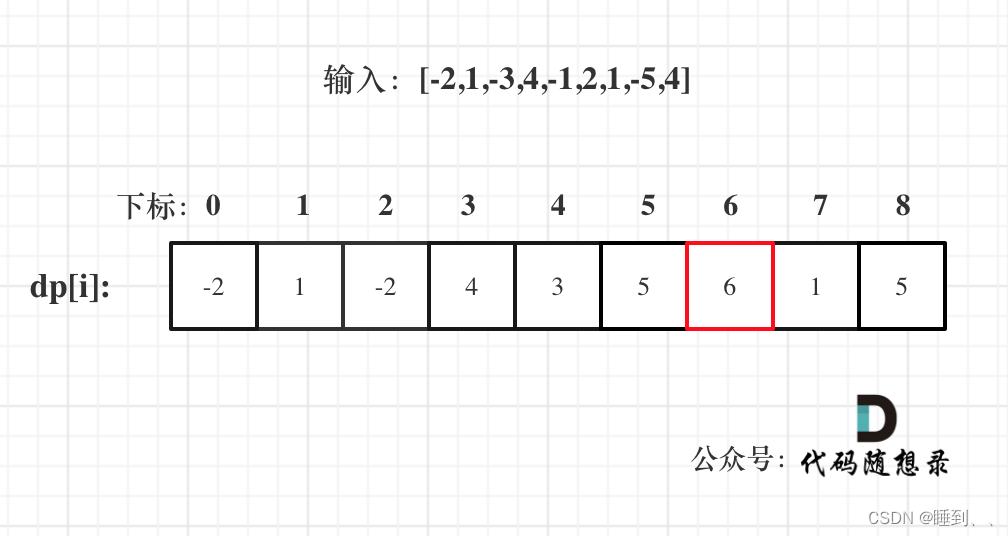
 * 举例推导dp数组
* 举例推导dp数组