本篇参考求二叉树叶子数与高度（C++）进行整理。

1. 二叉树中叶子数与高度

我们首先来看一看二叉树中叶子数与高度的定义：

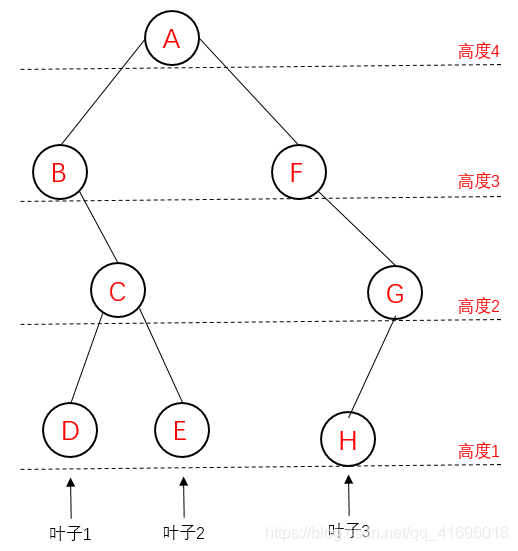
• 叶子数：对于一个二叉树的节点，若其既没有左子树又没有右子树，那它就是叶子节点。整个二叉树的叶子数为所有叶子节点个数。

• 高度：二叉树高度又称深度，其为根节点到叶子节点路径的最大值。
  

2. 求二叉树叶子数与高度的实现代码

求二叉树叶子数与高度均采用递归的方法，其基本操作方法都比较类似，具体实现代码如下：

#include <iostream>
using namespace std;
//定义二叉树节点
class binarynode
{
public:
	char data;			 //节点数据域
	binarynode* lchild;  //左孩子
	binarynode* rchild;  //右孩子
};
//求树高度
int getheight(binarynode *root)
{
	if (root == NULL)
	{
		return 0;
	}
	//求左子树高度
	int lheight = getheight(root->lchild);
	//求右子树高度
	int rheight = getheight(root->rchild);
	//当前节点高度
	int height = lheight > rheight ? lheight + 1 : rheight + 1;;
	return height;
}
//求叶子节点，采用递归方法
void calculateleafnum(binarynode* root, int* leafnum)
{
	if (root == NULL)
	{
		return;
	}
	if (root->rchild == NULL && root->lchild == NULL)
	{
		(*leafnum)++;
	}
	//左子树节点数目
	calculateleafnum(root->lchild, leafnum);
	//右子树节点数目
	calculateleafnum(root->rchild, leafnum);
}
//创建二叉树
void createtree()
{
	//创建节点
	binarynode node1 = { 'A',NULL,NULL };
	binarynode node2 = { 'B',NULL,NULL };
	binarynode node3 = { 'C',NULL,NULL };
	binarynode node4 = { 'D',NULL,NULL };
	binarynode node5 = { 'E',NULL,NULL };
	binarynode node6 = { 'F',NULL,NULL };
	binarynode node7 = { 'G',NULL,NULL };
	binarynode node8 = { 'H',NULL,NULL };
	//建立节点关系
	node1.lchild = &node2;
	node1.rchild = &node6;
	node2.rchild = &node3;
	node3.lchild = &node4;
	node3.rchild = &node5;
	node6.rchild = &node7;
	node7.lchild = &node8;
	//计算二叉树高度
	int height = getheight(&node1);
	cout << "二叉树的高度为：" << height << endl;
	//计算二叉树叶子数
	int num = 0;
	calculateleafnum(&node1, &num);
	cout << "二叉树的节点为：" << num << endl;
}

int main()
{
	createtree();
	system("pause");
	return 0;
}

运行结果：

3. 求二叉树叶子数与高度