FlashAttention 的速度优化原理是怎样的？
从 FlashAttention 到 PagedAttention, 如何进一步优化 Attention 性能
FlashAttention图解（如何加速Attention）
FlashAttention开源代码
Transformer Block运算量解析

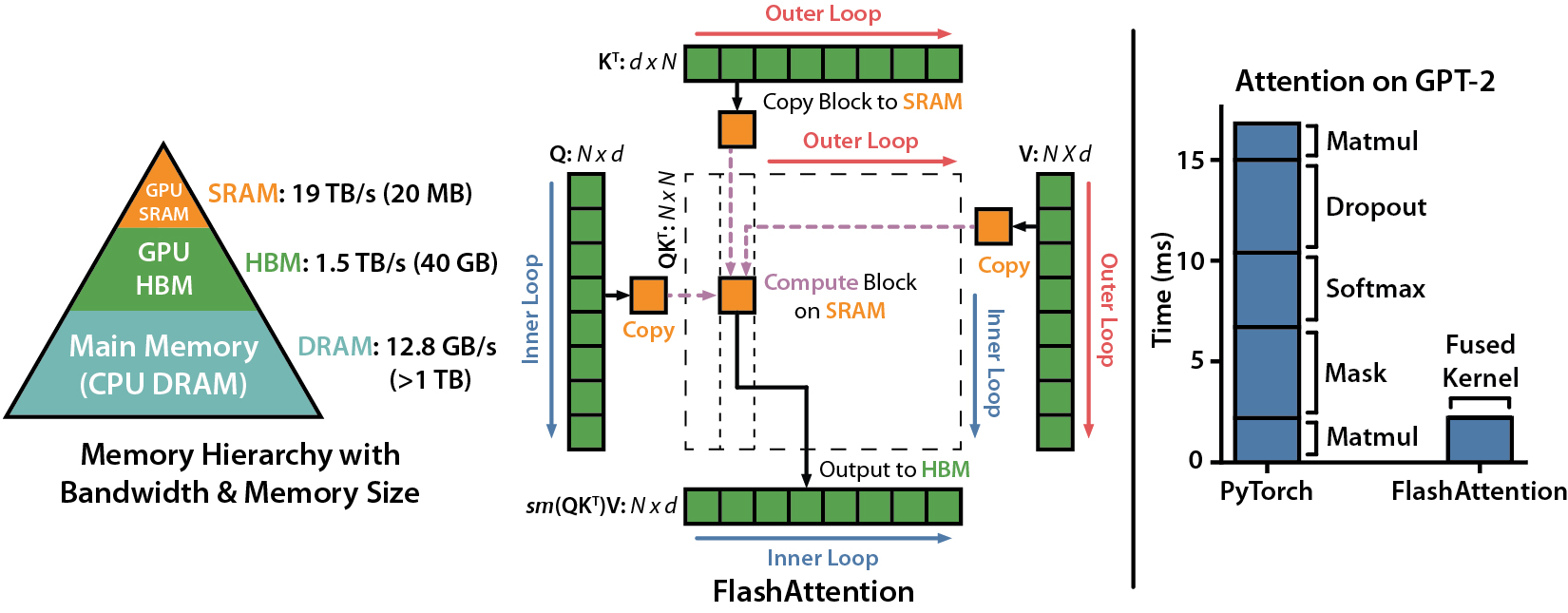
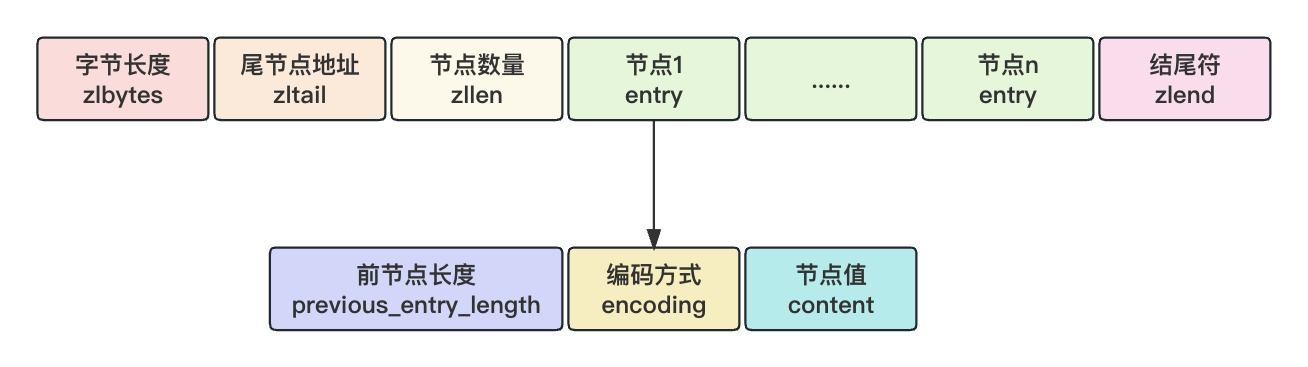
  在self-attention模块中，主要包含全连接层（通过矩阵乘法实现）、softmax（计算注意力权重），以及根据注意力权重的加权求和（计算注意力的输出结果）。其中，全连接层和根据注意力权重的加权求和其实都是通过矩阵乘法实现的，所以分块计算可以通过矩阵的分块乘法来实现。由于softmax的分母部分需要计算全局元素的求和，分块之后只能计算局部的和，导致softmax的分块计算变得复杂。

• 标准版softmax
  $$softmax(x)=\frac{e^{x_i}}{\sum e^{x_j}}$$

• 稳定版softmax
  $$softmax(x)=\frac{e^{x_i-max(x)}}{\sum e^{x_j-max(x)}}$$
    其中，$max(x)$表示 $x$ 中的最大值。

• 分块计算softmax

1. 将数值序列 $x$ 分成不同的块 $x^{(1)},x^{(2)},...,x^{(n)}$
2. 使用稳定版softmax计算第一块 $x^{(1)}$ 的结果，同时记录下第一块的最大值 $m(x^{(1)})$ 和第一块的局部求和结果 $l(x^{(1)})=\sum e^{x^{(1)}-m(x^{(1)})}$
3. 设置变量 $m_{max}$ 记录迭代到此的全局最大值，设置变量 $l_{all}$ 记录迭代到此的全局求和结果，后续随着迭代计算不同的分块 $x^{(i)}$ 逐步更新 $m_{max}$ 和 $l_{all}$。计算完第一块之后 $m_{max}=m(x^{(1)})$ , $l_{all}=l(x^{(1)})$
4. 使用稳定版softmax计算第二块 $x^{(2)}$ 的结果，得到 $m(x^{(2)})$ 和 $l(x^{(2)})=\sum e^{x^{(2)}-m(x^{(2)})}$
5. 更新迭代到此时的全局最大值 $m_{max}^{new}=max(m_{max},m(x^{(2)}))$
6. 更新迭代到此时的全局求和结果 $l_{all}^{new}=e^{m_{max}-m_{max}^{new}}\ast l_{all}+e^{m(x^{(2)})-m_{max}^{new}}\ast l(x^{(2)})$

  关于第 6 步的公式是怎么得到的，我们把第 6 步的公式拆解为两部分，现在我们计算到了第二块数据 $x^{(2)}$，所以我们此时的全局求和结果由两部分组成，第一部分是由 $x^{(1)}$ 数据块产生的求和结果，第二部分是由 $x^{(2)}$ 数据块产生的求和结果，但是 $x^{(1)}$ 和 $x^{(2)}$ 计算的求和结果分别使用的是各自局部的最大值 $max(x)$ 进行计算的，所以要将 $x^{(1)}$ 和 $x^{(2)}$ 的局部求和结果更新为当前阶段的全局求和结果。

  以更新 $x^{(2)}$ 的求和结果为例，在计算 $x^{(2)}$ 的softmax的过程中，分子分母同时除以了 $x^{(2)}$ 的局部最大值的 $e^{m(x^{(2)})}$，所以现在要对分母部分 $x^{(2)}$ 的局部求和结果进行还原，先乘以局部最大值的 $e^{m(x^{(2)})}$，然后在除以全局的最大值的 $e^{m_{max}^{new}}$，公式表示如下：
$$l(x^{(2)}{)}_{new}=\frac{\sum e^{x^{(2)}-m(x^{(2)})}\ast e^{m(x^{(2)})}}{e^{m_{max}^{new}}}=\sum e^{x^{(2)}-m_{max}^{new}}=e^{m(x^{(2)})-m_{max}^{new}}\ast l(x^{(2)})$$
  同理，也可以使用迭代到此时的全局的最大值的 $e^{m_{max}^{new}}$ ，更新数据块 $x^{(1)} 的局部求和结果为迭代到此时的全局求和结果 $ $l(x^{(1)}{)}_{new}$，表示如下：
$$l(x^{(1)}{)}_{new}=\frac{\sum e^{x^{(1)}-m(x^{(1)})}\ast e^{m(x^{(1)})}}{e^{m_{max}^{new}}}=\sum e^{x^{(1)}-m_{max}^{new}}=e^{m(x^{(1)})-m_{max}^{new}}\ast l(x^{(1)})$$

  所以，迭代到此时的全局求和结果就是 $l_{all}^{new}=l(x^{(1)}{)}_{new}+l(x^{(2)}{)}_{new}$ ，表示如下：
$$l_{all}^{new}=l(x^{(1)}{)}_{new}+l(x^{(2)}{)}_{new}=e^{m(x^{(1)})-m_{max}^{new}}\ast l(x^{(1)})+e^{m(x^{(2)})-m_{max}^{new}}\ast l(x^{(2)})$$

  因为在执行完数据块 $x^{(1)}$ 之后，我们保存了 $m_{max}=m(x^{(1)})$ , $l_{all}=l(x^{(1)})$ ，替换 $m(x^{(1)})$ 和 $l(x^{(1)})$ ，所以上式就等价为：
$$l_{all}^{new}=l(x^{(1)}{)}_{new}+l(x^{(2)}{)}_{new}=e^{m_{max}-m_{max}^{new}}\ast l_{all}+e^{m(x^{(2)})-m_{max}^{new}}\ast l(x^{(2)})$$
  上面这个公式，也就是上面第 6 步得到的公式。现在我们得到的 $ma{x}_{max}^{new}$ 就是迭代到当前数据块的全局最大值，$l_{all}^{new}$ 就是迭代到当前数据块softmax分母部分的全局求和结果。

7. 现在softmax的分母已经被更新成了全局的结果，现在就要把分子也更新成全局的结果就行了。分子的更新结果很简单，还是以更新 $x^{(2)}$ 的分子为例，在计算 $x^{(2)}$ 的softmax的过程中，分子分母同时除以了 $x^{(2)}$ 的局部最大值的 $e^{m(x^{(2)})}$，所以现在要对分子的结果进行还原，先乘以局部最大值的 $e^{m(x^{(2)})}$，然后在除以全局的最大值的 $e^{m_{max}^{new}}$，公式表示如下：
   $$\frac{e^{x^{(2)}-m(x^{(2)})}\ast e^{m(x^{(2)})}}{e^{m_{max}^{new}}}=f(x^{(2)})\ast e^{m(x^{(2)})-m_{max}^{new}}$$
     同理，更新后 $x^{(1)}$ 的分子如下：
   $$\frac{e^{x^{(1)}-m(x^{(1)})}\ast e^{m(x^{(1)})}}{e^{m_{max}^{new}}}=f(x^{(1)})\ast e^{m(x^{(1)})-m_{max}^{new}}$$

8. 现在就可以计算 $x^{(1)}$ 和 $x^{(2)}$ 迭代到此时的“全局”softmax了。
   $$softmax(x^{(1)}{)}_{new}=\frac{f(x^{(1)})\ast e^{m(x^{(1)})-m_{max}^{new}}}{l_{all}^{new}}=\frac{softmax(x^{(1)})\ast l(x^{(1)})\ast e^{m(x^{(1)})-m_{max}^{new}}}{l_{all}^{new}}$$
   $$softmax(x^{(2)}{)}_{new}=\frac{f(x^{(2)})\ast e^{m(x^{(2)})-m_{max}^{new}}}{l_{all}^{new}}=\frac{softmax(x^{(2)})\ast l(x^{(2)})\ast e^{m(x^{(2)})-m_{max}^{new}}}{l_{all}^{new}}$$
     上面公式中的 $softmax(x^{(1)}),softmax(x^{(2)}),l(x^{(1)}),l(x^{(2)}),m(x^{(1)}),m(x^{(2)}),m_{max}^{new}$ 等都是已知的中间结果，不用重新计算，也不用重新读取 $x^{(1)}$ 和 $x^{(2)}$ 数据块。

9. 将经过数据块 $x^{(1)}$ 和 $x^{(2)}$ 计算得到的 $m_{max}^{new}$ 和 $l_{all}^{new}$ 更新到 $m_{max}=m_{max}^{new}$ 和 $l_{all}=l_{all}^{new}$，将数据块 $x^{(1)}$ 和 $x^{(2)}$ 的计算结果看做一个整体作为 $x^{(1)}$，将读取的新数据块 $x^{(2)}$ 作为上面的 $x^{(2)}$，继续迭代下去，直到完成所有数据块的计算，这样就得到了全局的softmax结果
   

import numpy as np
import torch


def softmax(x):
    m_x = np.max(x)
    f_x = np.exp(x - m_x)
    l_x = np.sum(f_x)
    soft_x = f_x / l_x
    return m_x, f_x, l_x, soft_x


m_x1, f_x1, l_x1, soft_x1 = softmax(np.array([1, 2]))
m_x2, f_x2, l_x2, soft_x2 = softmax(np.array([3, 4]))
m_x_new = np.max([m_x1, m_x2])
l_new_all = np.exp(m_x1 - m_x_new) * l_x1 + np.exp(m_x2 - m_x_new) * l_x2
soft_x1_new = soft_x1 * l_x1 * np.exp(m_x1 - m_x_new) / l_new_all
soft_x2_new = soft_x2 * l_x2 * np.exp(m_x2 - m_x_new) / l_new_all
soft = torch.nn.functional.softmax(torch.Tensor([1, 2, 3, 4]), dim=0)

# [0.0320586  0.08714432] [0.23688282 0.64391426]
print(soft_x1_new, soft_x2_new)
# [0.0320586  0.08714432 0.23688284 0.6439143 ]
print(soft.numpy())