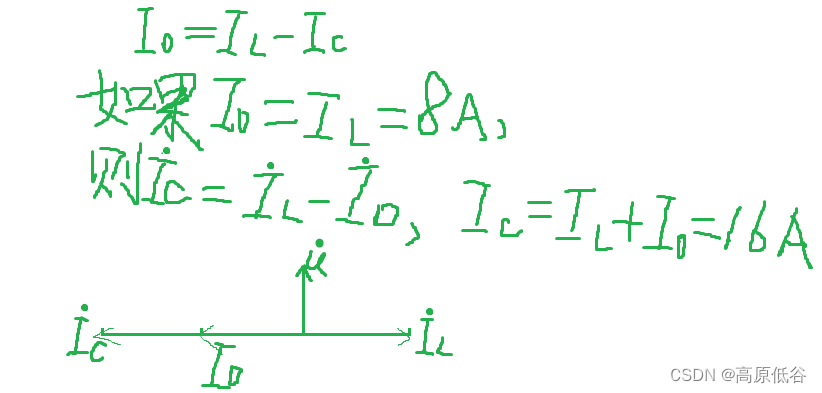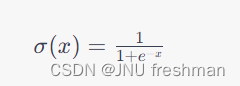8.1复数

复数可表示平面矢量、也可表示正弦量。特别是: 当复数表示正弦量的时候，此时复数称为相量。

8.2复数运算

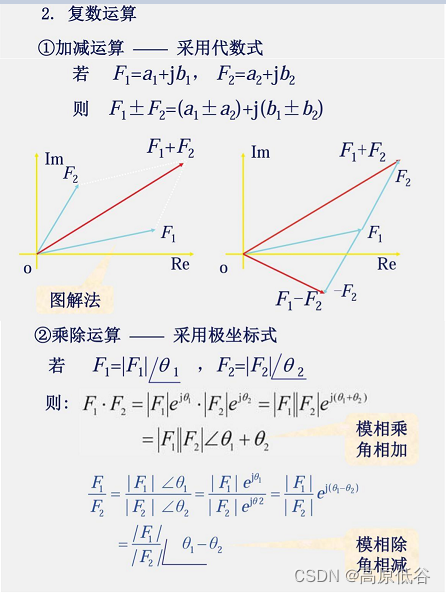
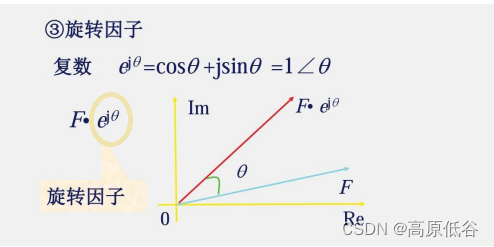
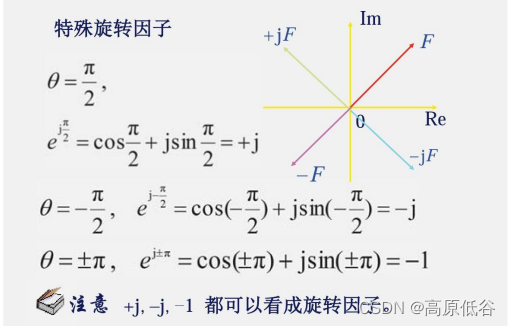
复数除法也可看做乘法，乘法的几何意义是旋转（辐角相加）( e^x + e^y =e^x+y)，同时伸缩（模变化）。

8.3正弦量

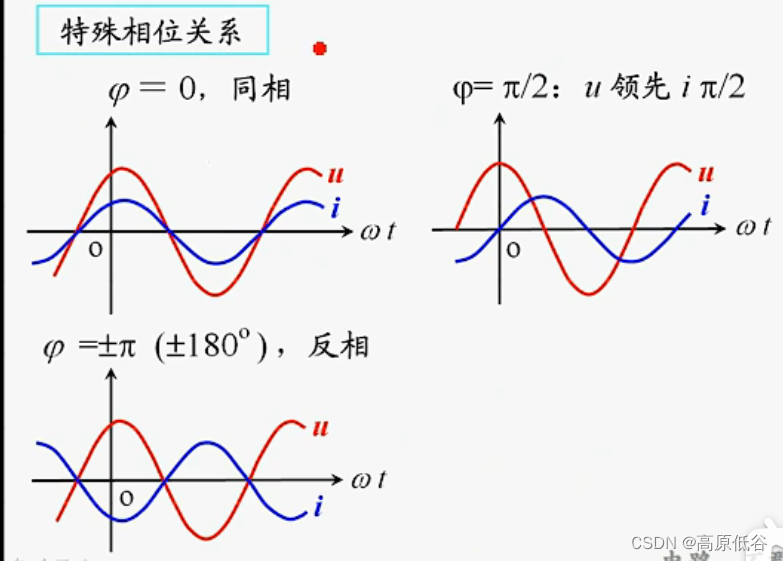
正弦和余弦没有实质的区别，正弦可以平移为余弦。
下面我们用余弦表示正弦。









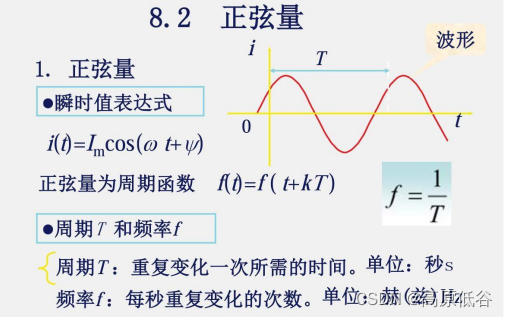
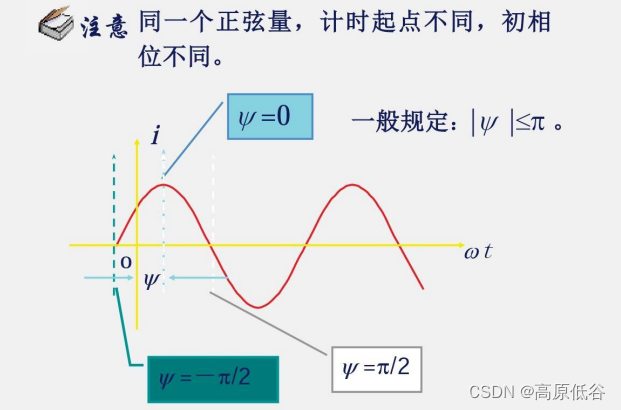
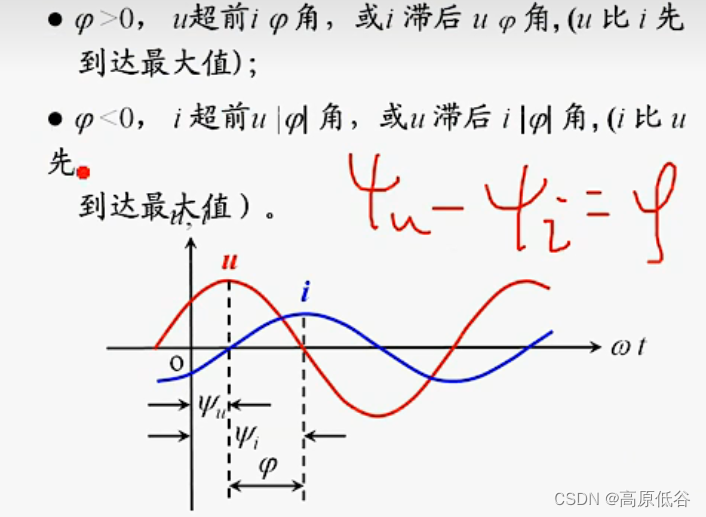
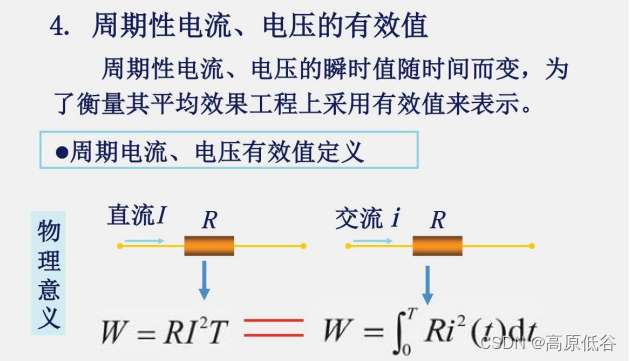
用做功相等定义等效

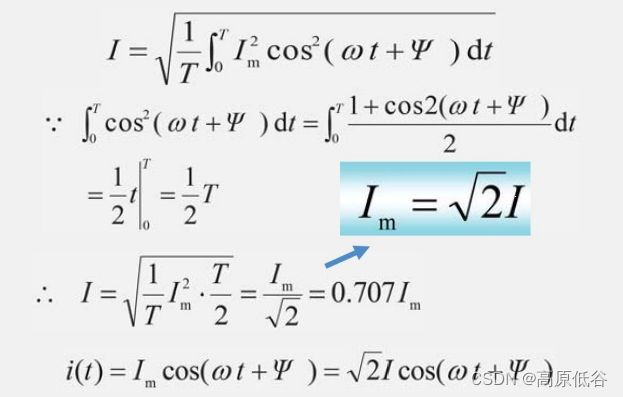
8.4相量法的基础

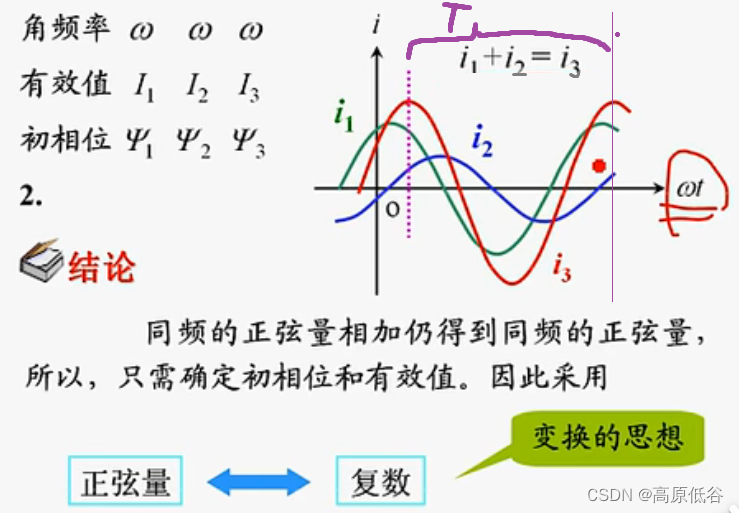
正弦量不考虑W，其他东西就和复数对应起来了。




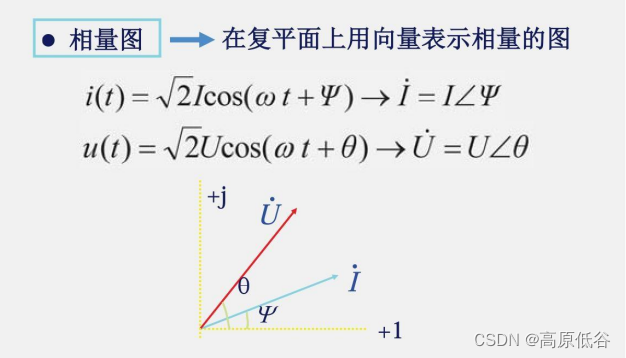
思想：为了求它，不求它，转而求其他，同时求得了它。

Re(x)代表对向量x取实部

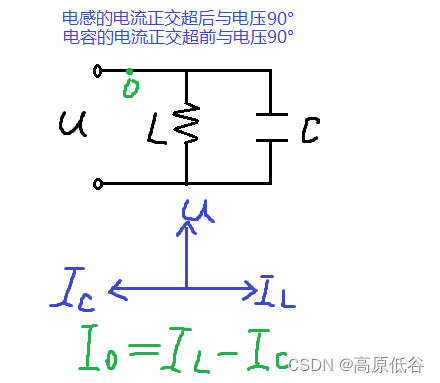
电流瞬间值等于电流有效值为模的向量

我们可以发现，和差化积的直接相加问题，转化为向量相加。

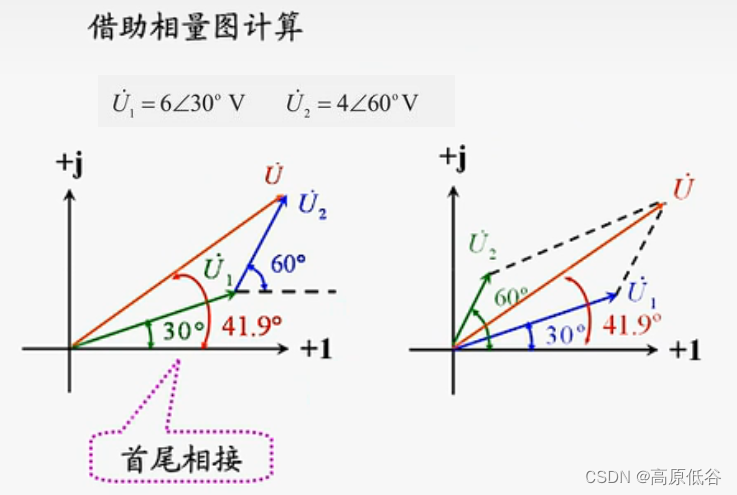
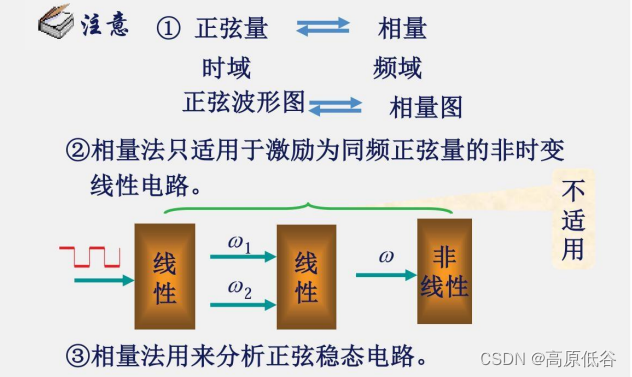
稳态且频率相同

8.5电路定律的相量形式

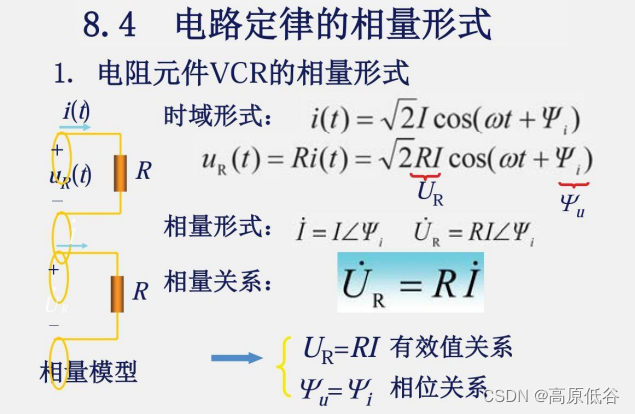
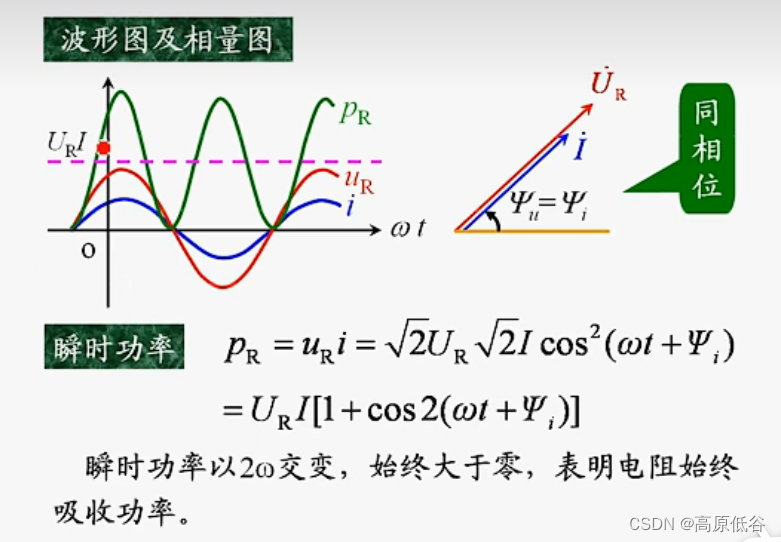
8.5.1电阻元件VCR的相量形式

VCR：voltage-current-relationship电压电流关系特性

8.5.1电感元件VCR的相量形式

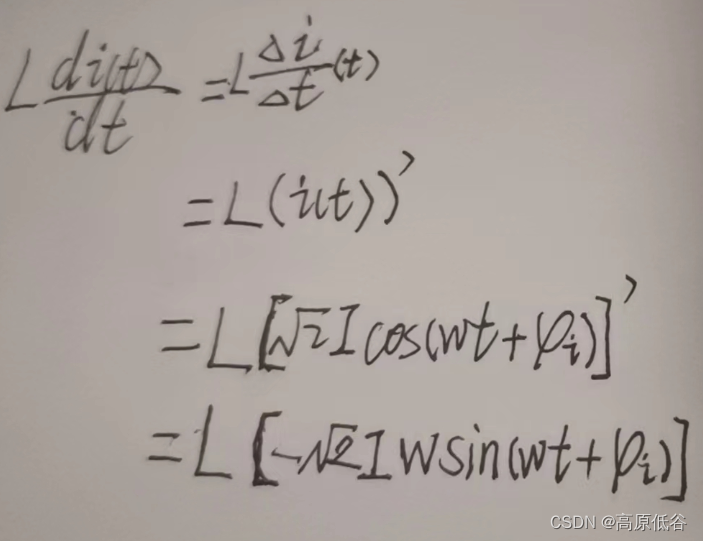
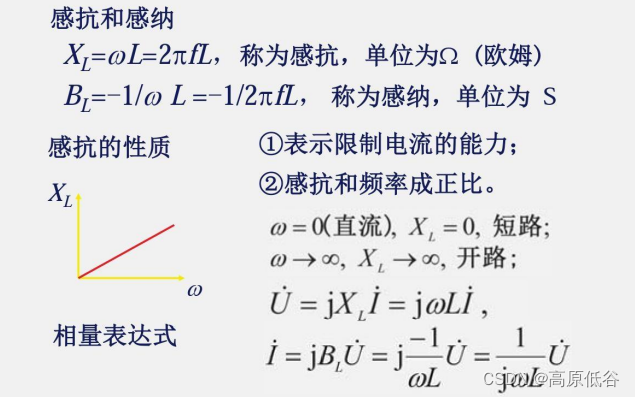
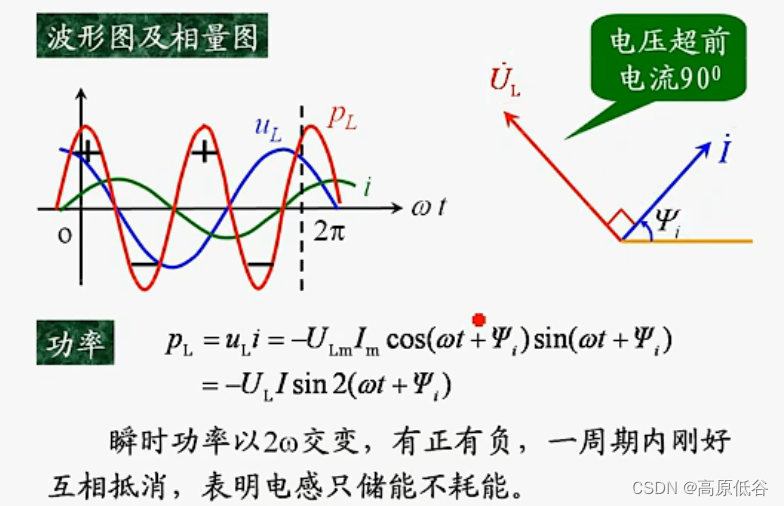
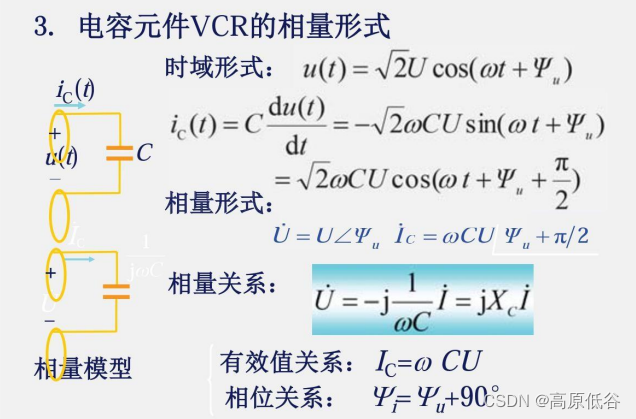
8.5.2电容元件VCR的相量形式

VCR：voltage-current-relationship电压电流关系特性

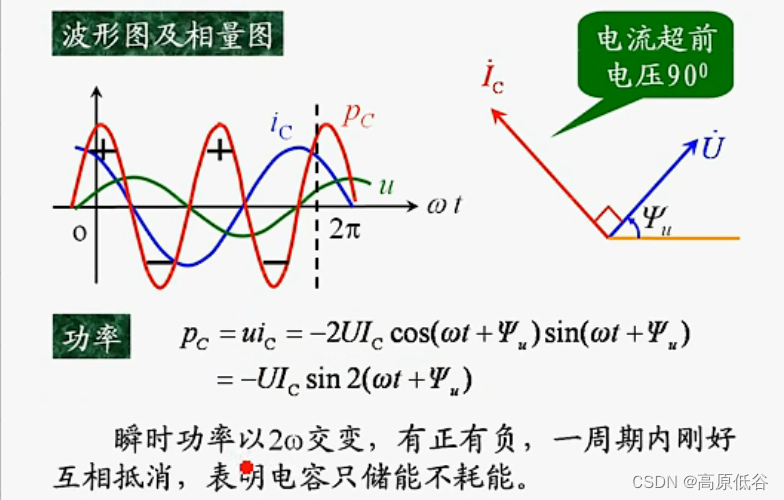
8.5.2基尔霍夫定律的相量形式

8.6例题

电流表测得的是有效值

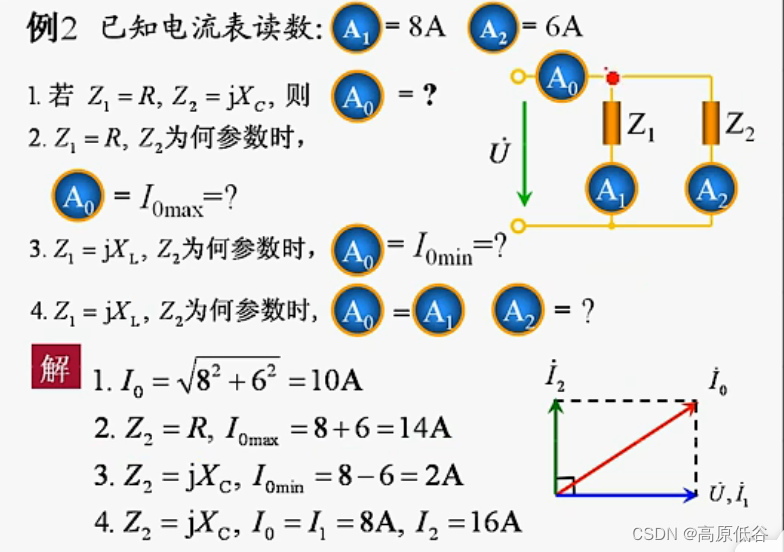
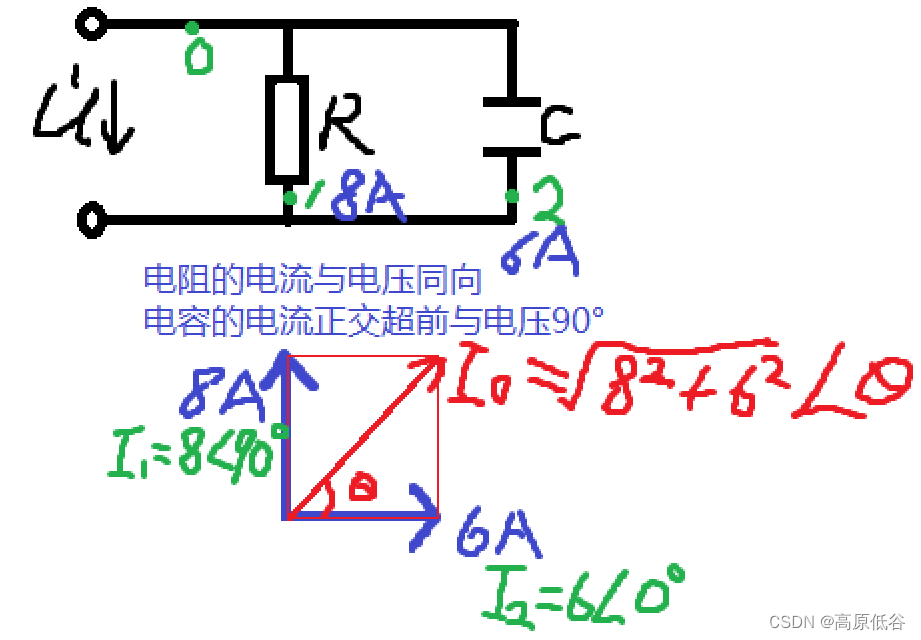
同向时最大，反向时最小。